CHEBFUN APPROXIMATION TO STRUCTURE OF POSITIVE RADIAL SOLUTIONS FOR A CLASS OF SUPERCRITICAL SEMI-LINEAR DIRICHLET PROBLEMS^∗

Abstract.

We use the Chebfun programming package to approximate numerically the structure of the set of positive radial solutions for a class of supercritical semilinear elliptic Dirichlet boundary value problems. This structure (bifurcation diagram) is provided only at the heuristic level in many important works. In this paper, we investigate this structure, as accurately as possible, for the class of problems mentioned above taking into account the dimension of Euclidean space as well as the physical parameter involved.

1. Introduction

We study the uniqueness and exact multiplicity of positive solutions $u\in C^2(B_n,ℝ)$ for the Dirichlet boundary value problem on a unit ball $B_n$ in ${ℝ}^n,n\ge 1$ ($x\in {ℝ}^n$) of the form

(1)

with $\lambda$ a positive parameter and

(2) $$f(u,ϵ):=\exp (u/(1+ϵu),$$

where $ϵ\in [0,1)$ is a parameter with physical significance.

For $ϵ=0$ and $n=1,2,3$ the above problem is the so-called Gelfand’s problem [5]. The parameter $ϵ$ has been introduced by Frank-Kamenetski and when $ϵ>0$ it has the physical significance of the reciprocal of the activation energy. The continuous solution $u(x)$ stands for the temperature in a chemical (catalysis) reaction.

Given the classical theorem of Gidas, Ni and Nirenberg [7] positive solutions of (1) are radially symmetric, i.e., $u=u(r),$ with $r:=|x|$, and moreover for all $r\in (0,1),$ and hence they satisfy

(3)

Quasilinear problems of type (1) arise in the theory of nonlinear diffusion generated by nonlinear sources, in the theory of thermal ignition of a a chemically active mixture of gases, in the theory of membrane buckling and in the theory of gravitational equilibrium of poly-tropic stars, to mention just a few applications.

Actually, the nonlinearity $f$ is derivable, increasing, convex and superlinear $\left({lim}_{s\to \mathrm{\infty }}\frac{f(s)}{s}=\mathrm{\infty }\right).$

In [10] the authors observe that if the growth rate of $f$ is greater than some critical exponents and the space dimension is higher (for example, $f(u):=\exp \left(u\right),{\left(1+u\right)}^p,p>1,1/{(1-u)}^k,k>0,\mathrm{\dots }$, for $n\ge 3$), then the bifurcation diagram can be very complicated even for the balls.

One of the most striking features of such problems is that positive solutions to (1) need not be unique. The exact multiplicity of positive solutions has been theoretically studied extensively in recent years, starting with Joseph and Lundgren [8], and continued by Bebernes, Eberly and Fulks [2] (and in some other papers by various authors).

Once a numerical solution to the problem (3) is found, say $u(r,\lambda ),$ it is called stable as all eigenvalues of the linearised problem are negative. The linearised problem around solution $u(r,\lambda )$ reads

(4)

When at least one is positive, that solution is called unstable.The technique of studying the linearized equation is not new, and some of them, relevant to the problem at hand, can be traced to early works by Chen and Lin [4].

We mention that we will focus in this paper on the cases of $n=2$ and $n=3.$

We will define a solution $u\left(r\right)$ of the problem (3) to be bell-shaped if it has a unique point of inflexion for $r\in (0,1).$

The bifurcation diagrams presented in [8], [2] or [9] may not be completely accurate.

The purpose of this work is to parallelize the analytical results with an accurate numerical study, i.e., to determine exactly the multiplicity of solutions, to draw some bifurcation diagrams and last but not least to calculate examples of solutions in various situations accurately.

Moreover, we can deduce the qualitative behaviour of the solution profiles with a change in any one of the physical parameters $ϵ$, $n$ and $\lambda$.

The paper is organized as follows. In Section 2 we summarize Chebfun as a MATLAB object-oriented software package. In Section 3 we consider the bidimensional case, find concave and bell-shaped solutions and plot some bifurcation diagrams for unperturbed and perturbed cases, i.e., vanishing and non-vanishing $ϵ$ respectively. In Section 4 we consider the tridimensional case and get our main results. We find accurately the turning points in the bifurcation diagram when $ϵ=0$ and show that for the larger values, i.e., $ϵ:0.1$ reduces to a simple fold one.

2. A concise review of Chebfun

For basic features of Chebfun, we refer to the book of Trefethen, Birkisson, and Driscoll [12]. The Chebfun software system represents functions and operators automatically as numerical objects. The BVP solver implements Newton’s method in function space and the derivatives involved are Frechet derivatives, not Jacobian matrices. The automatic differentiation techniques are used within the Chebfun class called chebop allows users to set up and solve nonlinear BVPs. Finally, the “nonlinear backslash” operator is used to solve the nonlinear algebraic system and consequently find the solution.

More details about the algorithms, design and performances of the Chebfun solver for BVPs are available in the paper [3]. Our own experience in using this solver is available in [6].

However, the process called pseudo-arclength continuation is implemented in the Chebfun by the code followpath. The idea of path-following is that we will not just vary a parameter such as $\lambda$, but we will follow a path of solutions (see [12] Ch. 18). The initial solution in this process is computed using the routine solvebvp and the necessary number of steps is determined on a case-by-case basis.

3. The case $n=2$

(a) A concave solution $n=2$, $ϵ=0$.

(b) The evolution of Newton’s iterates, $n=2$.

(c) The behavior of Chebyshev coefficients, $n=2$.

Figure 1. A concave and stable solution and its approximation.

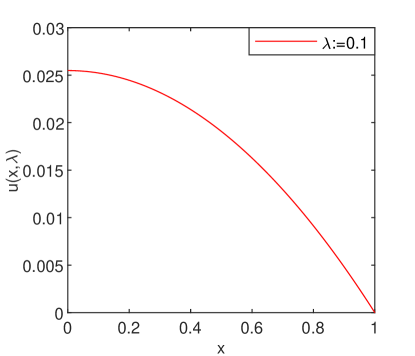
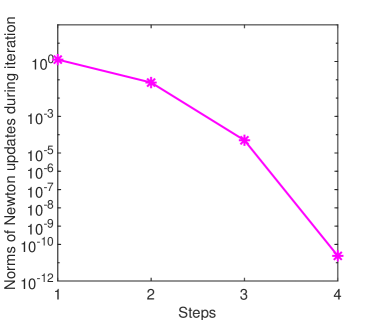
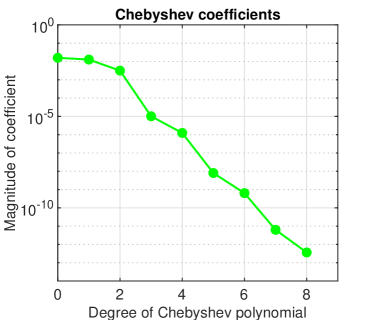
A concave solution for $n=2$, $ϵ=0$ is displayed in Fig. 1(a). The Chebfun operatorial error in computing this solution has been of order ${10}^{-12}.$ Newton’s method in solving the nonlinear algebraic system is clearly of order two (see Fig. 1(b)) and the convergence of Chebyshev collocation implemented by Chebfun is exponential as it is apparent from Fig. 1(c).

It is worth noting now that simple initial data, equating a constant leads to these results. Moreover, the solution is stable because all the attached eigenvalues of the problem (4) are negative.

(a) A bell-shaped solution $n=2$, $ϵ=0$.

(b) The evolution of Newton’s iterates, $n=2$, $ϵ=0$.

(c) The behavior of Chebyshev coefficients, $n=2$, $ϵ=0$.

Figure 2. An unstable bell-shaped solution and its approximation.

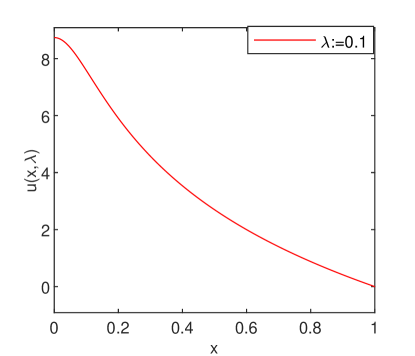
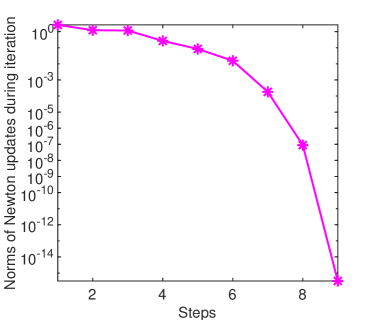
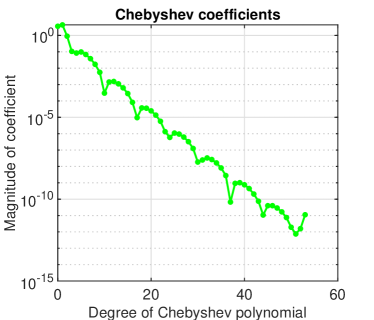
A bell-shaped solution for $n=2$, $ϵ=0$ is displayed in Fig. 2(a). The Chebfun operatorial error in computing this solution has been only of order ${10}^{-6}.$ Newton’s method in solving the nonlinear algebraic system remained of order two (see Fig. 2(b)) and the convergence of Chebyshev collocation implemented by Chebfun is somewhere between exponential and algebraic, as it is apparent from Fig. 2(c).

It is worth noting now that simple initial data, equating a constant do not lead to a bell-shaped solution. It took many numerical experiments to find initial data that would lead Chebfun to such a solution. In the end, we found a second-degree polynomial that satisfies the boundary conditions in the problem (3).

Moreover, the solution is unstable because all the attached eigenvalues of the problem (4) are negative except one which is positive.

(a) Bifurcation diagram $n=2$, $ϵ=0$.

(b) Bifurcation diagram when $n=2$ and ”small” $ϵ$. Chebfun code followpath attained a maximum of $92$ steps.

(c) Bifurcation diagram when $n=2$ and ”large” $ϵ$. Chebfun code followpath attained a maximum of $300$ steps. ${\lambda }_{max}$ computed equals now $2.26040973.$

Figure 3. Bifurcation diagrams for various $ϵ$ when $n=2$.

Incipient numerical results in solving the disturbed problem (2) can be traced back to the beginning of the ’60s in the work of Parks [11].

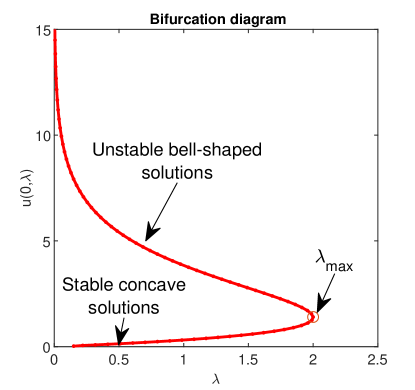
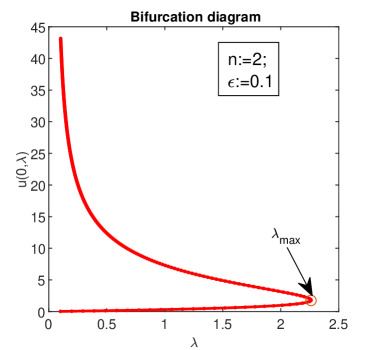
Three bifurcation diagrams, i.e., the dependence of the scalar measure $u(0,\lambda )$ (supremum norm of the solution $u$) on $\lambda$ are depicted in Fig. 3. The solutions branches in all these plots as $\lambda$ approaches ${\lambda }_{max}.$ In some sense they bend around to turn back into the other direction, making $u(0,{\lambda }_{max})$ a double-valued function of $\lambda .$

Conceptually these figures are identical, the only difference is that ${\lambda }_{max}$ grows with $ϵ$ as this parameter approaches unity. Along with [2] we introduce the ”invariant”

(5) $$I(a,\lambda ):=c^2+4c+2\lambda ,$$

where $c=c(a,\lambda ):=u^{\prime }(1,a,\lambda )$ and $a:=u(0,\lambda ).$ The bifurcation diagram can be summarized as follows:

• for $\lambda \in (0,{\lambda }_{max})$, there exist two solutions;

• for $\lambda ={\lambda }_{max}$ there exists one solution;

• for $\lambda >{\lambda }_{max}$ there are no solutions;

• the ”invariant” $I(a,\lambda )=0$ is satisfied with an error of order ${10}^{-12}.$

These results are in perfect agreement with those reported in the paper [2].

It is important to observe that when $ϵ=0$ the followpath code stops after $92$ steps with a warning message about a failure in solving the linear algebraic system. The number of steps accepted by this code increases with $ϵ$ that is, when the problem becomes less critical (see Fig. 3).

4. The case $n=3$

The bifurcation of solutions is much more complicated in this case than in the previous one. We will analyse two distinct situations.

4.1. The unperturbed source

The concave or bell-shaped solutions computation in this case does not differ from the previous case. For this reason, we will not address this issue.

As far as bifurcation diagrams are concerned, things are quite different. Thus, we begin with the case $ϵ=0$ in (2).

Figure 4. Bifurcation diagram when $n=3$ and $ϵ=0.$

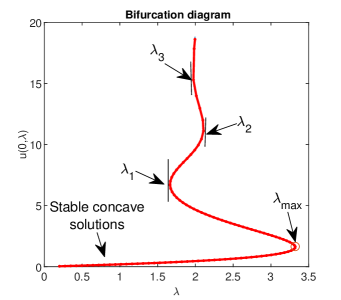
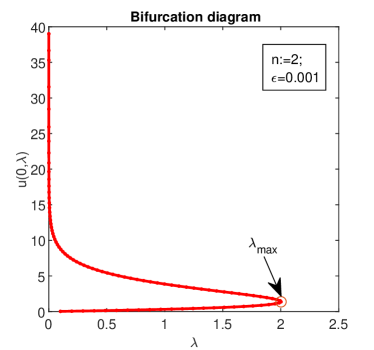
In this case, Chebfun has found the following values for turning points in Fig. 4:

$${\lambda }_1=1.664158,{\lambda }_{max}=3.321987,{\lambda }_2=2.108171,{\lambda }_3=1.972368.$$

Moreover, we can state that:

• for one stable solution; and for $\lambda >{\lambda }_{max}$ there are no solutions;

• for there are two solutions;

• for there are three solutions;

• for there are a countable (?) infinity of solutions;

• at each point ${\lambda }_{max}$,${\lambda }_1,$ ${\lambda }_2,$ and ${\lambda }_3$ there is a solution to unperturbed problem i.e., $ϵ=0$ in (2).

4.2. The perturbed source

We now comment on the case of non-vanishing $ϵ$ in (2). It is also worth noting that when $ϵ$ is close to zero, i.e., $ϵ=𝒪\left({10}^{-4}\right)$ or smaller the bifurcation diagram has the same aspect as that in Fig. 4.

The situation changes radically when $ϵ$ increases. Thus for $ϵ=0.1$ Chebfun found the diagram from Fig. 5.

Figure 5. Bifurcation diagram when $n=3$ and $ϵ=0.1$. Chebfun has computed ${\lambda }_{max}=3.77418342.$

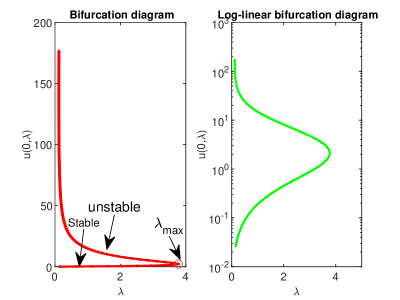
We must say that we have not found anywhere in the literature the numerical values for these turning points. There is only the information that ${\lambda }_{max}>\overline{\lambda }=2\left(2-n\right),$ a condition that in our case is fully satisfied.

The right-hand panel of Fig. 5 displays the same bifurcation diagram but in a semilogy linear plot.

5. Concluding remarks and open problems

The question of finding an appropriate initial starting guess when solving a nonlinear BVP remains an open and quite time-consuming one. However, in all the problems addressed, the operatorial error did not decrease under the order ${10}^{-8}.$

On the other hand, to some extent, the pseudo-arclength method implemented with Chebfun has worked fairly well. Efforts to improve the efficiency of the continuation code will probably lie in the linear solvers (the same conclusion as in [9]). This is because to solve some bifurcation issues, Chebfun issued the following: Warning: Linear system solution may not have converged.

However, we believe that for the most difficult situation, i.e., $n=3,$ we have considerably improved, in terms of accuracy, the bifurcation diagrams from literature (see for instance [9] and [2]).

Acknowledgements.

We gratefully acknowledge the helpful remarks of the referee.