Modified adaptive quadrature by expansion
for Laplace and Helmholtz layer potentials in 2D∗
Abstract.
An adaptive algorithm based on quadrature by expansion (QBX) is proposed for computing layer potentials at target points near or on a smooth boundary in . The algorithm can be viewed as a major modification to the two-phase algorithm AQBX, proposed recently by Klinteberg et al. [SIAM Journal on Scientific Computing, 40(3), 2018]. In the modified AQBX (MAQBX), we consider sharper bounds for the involved truncation error. As a result, the involved stopping criteria are met earlier, and the total computational cost is reduced. Moreover, MAQBX is a single-phase algorithm and its structure is far simpler than that of AQBX. It is recommended that QBX (or any version of it) should be applied on a small part of the boundary that is near the target point, and a classical quadrature is applied on the rest of the boundary (this is often referred to as local QBX). We partially show that for Laplace and Helmholtz potentials, parametric symmetry of the target point with respect to the near part, can improve the convergence of QBX. Based on this observation, we suggest the local MAQBX that is very efficient in practice both for computing layer potentials and for solving boundary integral equations via the Nyström scheme.
Key words and phrases:
quadrature by expansion; layer potential; Laplace problem; Helmholtz problem; adaptive quadrature.2005 Mathematics Subject Classification:
65R20; 65D30; 65D32In boundary integral methods (BIMs), one uses Green theorems and transform a boundary value problem (BVP) for PDEs to a well-posed integral equation on the boundary of the domain of definition of the problem (note that the domain of application of BIMs extends far beyond the scope of PDEs). This has many advantages over the traditional volume PDE solvers such as FD, FEM, etc: 1) the dimension of the problem is reduced by one, so one needs fewer sample points to achieve a given accuracy, 2) an exterior problem with an unbounded spatial domain is reduced to a boundary integral equation over a bounded domain, 3) solving integral equations of the second kind is more numerically stable than solving PDEs directly by traditional discretization methods, 4) through the Nyström method, the problem of solving an integral equations of the second kind is reduced to the simpler problem of numerical quadrature or cubature for which high-order rules exist, 5) moving boundaries can be handled more easily, 6) a boundary integral formulation reflects well-posedness of the underlying physical problem more fairly, etc.
Assume that is the fundamental solution of the PDE associated with a BVP defined in a domain , . In a BIM, the solution of the problem is represented as a layer potential with a jump discontinuity on the boundary . This jump discontinuity is essential in well-posedness of the resulting boundary integral equation. Consider the double layer potential
| (1) |
(with the outer unit normal at ) and the single layer potential
| (2) |
The double layer potential itself and the gradient of the single layer potential satisfy jump discontinuity properties. Thus, the double layer and the single layer potentials are suitable for Dirichlet and Neumann problems, respectively. For the sake of solvability, one usually uses a combined field representation
| (3) |
where is a coupling parameter. For a Dirichlet problem with the Dirichlet data on the boundary, we obtain the following boundary integral equation for the unknown density function :
| (4) |
where the positive and the negative signs correspond to the exterior and the interior problem, respectively. If is an approximate solution of (4), the solution to BVP at the target point is achieved by computing the layer potential . For Neumann and Robin boundary conditions, BIM is also led to integral equations of the second kind, which are known to be well-posed (see [11] and references therein).
In this paper, we focus on two-dimensional Laplace and Helmholtz problems, though the theory is readily applicable to other problems.
In BIM, singularity is a price which should be paid for well-posedness. Indeed, the singularity of the fundamental solution yields the jump discontinuity property of the layer potential, and the latter causes the term in (4), which renders the boundary integral equation to a well-posed integral equation of the second kind. Singularity of the fundamental solution is inherited by both the boundary integral equation and the layer potential. Indeed, the boundary integral equation is weakly singular, and the layer potential at a target point near the boundary is a nearly singular integral. There are several efficient numerical methods for both the problems (see e.g., [5, 7, 8, 9, 10, 13, 14, 15, 16, 18, 22]), but there is still the need to design more robust algorithms.
Quadrature by expansion (QBX) was introduced in [17] for computing layer potentials at target points on or near the boundary. QBX is easy to implement, high order accurate, and despite earlier methods, dimension-independent. Moreover, QBX can be coupled with fast multipole methods (FMMs) and introduce fast algorithms for both the problems of solving boundary integral equations and computing layer potentials at target points near the boundary. In QBX, the singular integrand is locally expanded about a center with a suitable distance from the boundary. As a result, the singular or nearly singular layer potential is approximated by a sum of several regular integrals. Due to its individual benefits, QBX has been the subject of many studies for the last decade. In [6, 12, 3], convergence of QBX is studied in depth. Some combinations of QBX with FMM are suggested in [26, 25, 20]. QBX has also found applications in simulating spheroids in periodic Stokes flow [2]. For other applications and modifications of QBX one can see [4, 21, 23, 27].
One of the difficulties of QBX is the choice of parameters to achieve the optimal accuracy. The distance of the expansion center from the boundary, the order of the expansion, and the number of abscissas for the underlying quadrature have unspecific interactions on the total accuracy. For example, when grows, the total error can decreases or increases depending on the values of and . Thus, there is an urgent need to determine optimal parameters to achieve a given accuracy.
In [4], this problem has been studied in depth, and an adaptive algorithm is proposed for determining and , for a given . In adaptive QBX, the potential is written as the inner product of a vector of coefficients involving regular integrals over the boundary and a vector of norm one. The error in QBX can be separated into a truncation error and a coefficient error. In adaptive QBX, practical a priori estimates for both of the errors are suggested, which enable one to determine the optimal parameters in order to achieve a given accuracy. The algorithm has two phases. In the first phase, the coefficients are computed by the Gauss-Legendre rules to a given accuracy. In the core of this phase, there is a usable and sharp a priori error estimate for the Gauss-Legendre quadrature. The idea is developed by contour integrals and residue calculus, which was extended later to curves and surfaces in [1, 24]. Meanwhile, the coefficients are computed till a stopping criterion is met for the truncation error. In the second phase, the potential is computed by considering a different stopping criterion for the truncation error. Indeed, in the first phase, an upper bound is employed for the truncation error to compute coefficients contributing in the second phase, while in the second phase, a sharper bound is used to evaluate the potential. This causes that some coefficients are computed in the first phase that do not have any contribution in the second phase, and this in turn exposes an extra and unnecessary computational cost.
In the present paper, we address the above issue. If we consider the sharper bound in both the phases, then they merge into a single one, resulting a modified algorithm that is simpler as well as faster in practice. We also propose some other modifications which improve the logic and convergence of adaptive QBX. The estimate suggested in [4] for the coefficient error actually depends on . Here, we suggest a -independent one, which gives a more reasonable bound for the coefficient error. Also, we partially show that for Laplace and Helmholtz potentials, if some symmetry conditions are hold, the convergence of QBX is improved. Such conditions can easily be hold without imposing an extra computational cost.
The rest of paper is organized as follows. In Section 1, a brief review of QBX is given. Section 2 contains the modifications to the AQBX algorithm of [4], based on which, we devise the modified AQBX (MAQBX) algorithm in Section 3. We carry out some numerical experiments in Section 4 to illustrate the efficiency of the MAQBX algorithm for computing layer potentials as well as solving boundary integral equations. Finally, we give some conclusions in Section 5.
1. QBX
In this section, we give a review of QBX and its localization. Assume that is either interior or exterior of a bounded domain in with smooth boundary . In 2D, it is more convenient to consider as the complex plain and write the potentials in the complex setting. Assume that is an analytic -periodic counterclockwise parametrization of the boundary, that is . Assume also that the boundary is so smooth that never vanishes. Then, the outer normal at any point , is determined by .
In the complex setting, a 2D layer potential can be written in form of
| (5) |
where is the target point in , is a linear combination of the fundamental solution and its normal derivative, and is the arc length element with respect to .
The main assumption of QBX is that the variables of can be separated by a known addition theorem as
| (6) |
where and are either scalars or 2-vectors with given , the distance of the expansion center from the boundary. Note that is unbounded for any , thus the expansion (6) should have a singular factor. We assume that is bounded and is the singular part, i.e., is unbounded for any . We also assume that (6) is normalized as
| (7) | |||
| (8) |
for and integer . This normalization is necessary in adaptive QBX (see [4]).
Since the expansion center is far away from the boundary, the integrals (10) are regular and can be approximated by classical quadrature rules to the given accuracy. Assume that , for each , is approximated by . When the distance of from the boundary is less than , the can be approximated by QBX as
| (11) |
The total error is the summation of the truncation error () and the coefficient error ():
| (12) |
See [12] for an error analysis. In practice, the truncation error decreases almost exponentially as when grows. The coefficient error depends on the accuracy of the underlying quadrature rule, but it can be deteriorated as increases. The interplay between and , as grows, naturally leads us to search for the optimal , which minimizes the total error.
The paper [4] was the first attempt to study this problem in depth, and here, we give some revisions to the algorithm proposed in [4]. Before that, we complete this section by determining and for Laplace and Helmholtz layer potentials.
1.1. Laplace double layer potential
Fundamental solution of the 2D Laplace problem is . In the complex setting, the corresponding double layer potential can be written as , where
| (13) |
Now, from the Taylor expansion
| (14) |
the corresponding and is specified
| (15a) | ||||
| (15b) | ||||
1.2. Laplace single layer potential
In the complex setting, the Laplace single layer potential can be written as , where
| (16) |
Now, from the Taylor expansion
| (17) |
the corresponding and is specified by
| (18a) | ||||
| (18b) | ||||
| (18c) | ||||
1.3. Helmholtz double layer potential
In the complex setting, fundamental solution of the 2D Helmholtz problem with the wave number is
| (19) |
For Helmholtz potentials, one uses the Graf addition theorem [19, §10.23(ii)],
| (20) |
where and are polar coordinates of and , respectively, i.e.,
| (21a) | ||||
| (21b) | ||||
| (21c) | ||||
| (21d) | ||||
Then, the corresponding and are given as follows (see [4])
| (22a) | ||||
| (22b) | ||||
| (22c) | ||||
| (22d) | ||||
where
| (23) |
and
| (24) |
for all . Note that and are 2-vectors for
1.4. Helmholtz single layer potential
1.5. Localization
For integration of (5), one can split the integration path as into the ‘near part’ and the ‘far part’. The near part contains points of the boundary which are so near the target point , that classical quadrature rules on with a moderate number of abscissas leads to rather large error. More precisely, for a given integer ,
| (27) |
Discussion on the choice of is beyond the scope of this article; interested reader can refer [6, 4] for some comments.
It is recommended that QBX is used only on the near part, and a traditional fast quadrature rule is employed for the far part [6, 4]. This is the so-called local QBX that is compatible with FMM. In local QBX, one divides the boundary into smaller pairwise disjoints panels,
| (28) |
such that the boundary is well-resolved by the panels, i.e., the curvature of each panel is rather small. One often uses panels of equal length though panels of different lengths are also allowed. In the latter case, it is recommended that the lengths of any two adjacent panels have a ratio in the interval (see [20] for more details).
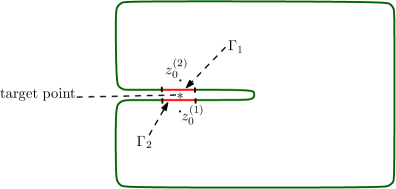
Note that the near (or far) part of a boundary with respect to a target point is not necessarily connected. In Fig. 1, the near part is the union of two disjoint curves and . QBX is applied for each panel separately with an individual expansion center, i.e., for the panel , for . Without losing any generality, we assume that the near part is always connected throughout this paper.
In adaptive local QBX, the only input parameter is the error tolerance . In Section 3, we suggest how to choose and determine the near part by . Throughout the paper, by adaptive QBX, we mean adaptive local QBX, and the idea is described on a typical small panel that is near to the target point and in front of it, i.e., the set takes its minimum at a point in . Here, is an open ball of radius centered at .
2. Some improvements in adaptive QBX
In this section, we give some modifications to the two-phase algorithm proposed in [4] for adaptive QBX. In Section 2.1, the first phase, i.e., the coefficient error, is affected by considering more suitable criteria for the coefficient refinement. In Section 2.2 and Section 2.3, we modify the second phase such that the truncation error reaches the stopping threshold more rapidly. In total, one obtains a single-phase algorithm for adaptive QBX (ref. Section 3) that is simpler and faster than that of [4].
2.1. -independent coefficient error estimate
In the algorithm proposed in [4], the quadrature rule is refined so that for each , where is a given tolerance. This strategy has this disadvantage that the upper bound for the coefficient error grows linearly with . Indeed,
| (29) |
If we use the condition for each instead, then we gain two advantages. Firstly, approximates more accurately since it is assumed that decays exponentially by . Secondly,
| (30) |
Thus, the upper bound (30) is independent of .
Note that may reach the machine epsilon rapidly as grows. In order to avoid extra effort, one can consider the condition instead. Since one does not expect that exceeds, e.g. 50, the inequality (30) will still be valid up to a tolerance scalable to the machine precision.
In order to approximate to a given accuracy, we suggest the Gauss-Legendre rules, though any other quadrature rule can also be employed, provided that there exists a practical error bound for it that contains no unknown coefficients and can efficiently be evaluated. In [4], the authors suggest such an a priori estimate of , where is an approximation of obtained by the -point Gauss-Legendre quadrature rule:
| (31) |
where is a parametrization of , and is a zero of the complex function . For details on how to approximate and evaluate robustly, one can see [4, Section 3.1].
2.2. Avoid computing extra coefficients
Truncation error depends on the coefficients , which are unknown. Assume that is an approximation of for each .
The algorithm proposed in [4] has two phases. Since it is assumed that the coefficients decay exponentially as grows, one can expect that their approximate values do so. In the first phase ([4, Algorithm 1]), starting from , the coefficients are approximated by to the accuracy of till they drop below . If is the smallest integer such that , then set . Thus, by [4, Eq. (14)],
| (32) |
In the second phase ([4, Algorithm 2]), only those terms with are contributed in the sum (11). This means that there is a possibility that some coefficients are computed in the first phase but do not contribute in the second phase since . In this case, the value of is updated in the second phase, accordingly.
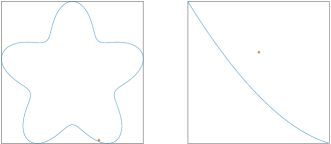
For example, consider a small portion of the starfish
| (33) |
between , and the target point (see Fig. 2). For computing the Laplace double layer potential by QBX, as recommended in [4], let with denoting the length of . The number of computed coefficients at the end of the first phase (num-coeff-phase1) and the number of contributed terms in the approximate potential (11), i.e., , for each tolerance are listed in Table 1. The differences between the values of these two rows indicate that a considerable portion of computational cost is devoted to computing some coefficients which never come to use.
| num-coeff-phase1 | 5 | 6 | 7 | 9 | 10 | 12 | 14 | 15 | 17 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 5 | 6 | 7 | 8 | 8 | 9 | 10 |
We can revise the above procedure by approximating by to the accuracy of (see Section 2.1) till drops below . Let be the smallest integer such that . Then, setting ,
2.3. Expansion center
Our observations show that position of the target point with respect to the curve affects the efficiency of adaptive QBX. Indeed, the more symmetric the target point is with respect to , the earlier the condition is satisfied. Note that this symmetry is not necessary geometrically, and it should be viewed in the sense of parametrization. In order to explain the idea, we need the following lemma.
Lemma 1.
Consider a holomorphic function on the lines , for some . Assume that satisfies the following conditions in its domain of analyticity: (c1) ; (c2) either or . Then, the real-valued function defined by
| (34) |
on , is even.
Proof.
Change of the variables with (c1) and (c2) yields
| (35) |
∎
Thus, under the assumptions of Lemma 1, is a critical point of . In the following, we use Lemma 1 to show that the coefficients in either of the Laplace or the Helmholtz layer potentials, are minimized for almost all , when the projection of the target point on , has the preimage in the middle.
2.3.1. Laplace potentials
Assume that is a parametrization of , i.e., . Then, for any , the coefficient , corresponding to the Laplace double layer potential, can be written as
| (36) |
where , , and is the expansion center. When the length of is small enough and it resembles a straight segment in the complex plain, we can assume that is almost constant on , and is approximated by a line, i.e.,
| (37) |
for some . Then,
| (38) |
Similarly, for the Laplace single layer potential
| (39) |
Note that satisfies all the assumptions of Lemma 1. Thus, , as a critical point of the factor
| (40) |
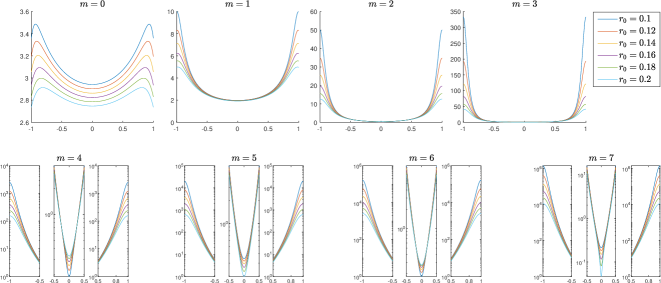
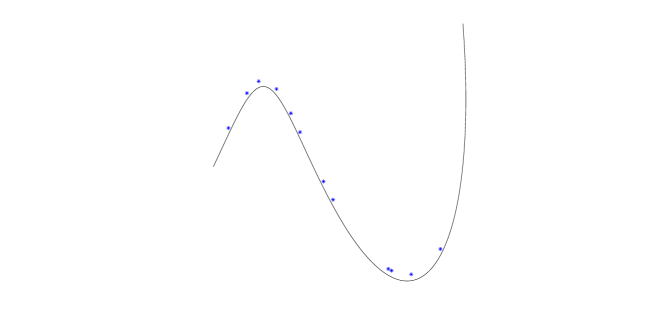
may potentially minimize , though we could not establish any result about it. However, our numerical experiments are all in accordance with this claim. In Fig. 3, for some different values of , we have plotted , for , as functions of .
Because of the linear assumption (37), one can imply that is almost the closest point of to . Therefore, according to the discussion above, the best position of the near part with respect to the target point is such that lies near the midpoint of the preimage , where stands for the closest point of to (see Fig. 4).
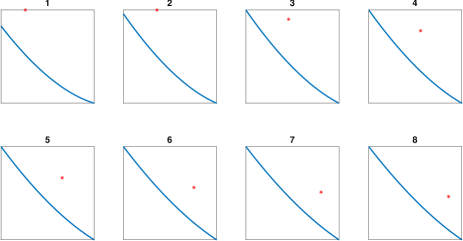
| Fig | midpoint | Fig | midpoint | ||||
|---|---|---|---|---|---|---|---|
| 16 | 13 | ||||||
| 1 | 5.15 | 59 | 5 | 5.11 | 33 | ||
| 93 | 94 | ||||||
| 14 | 14 | ||||||
| 2 | 5.14 | 56 | 6 | 5.10 | 56 | ||
| 93 | 93 | ||||||
| 13 | 15 | ||||||
| 3 | 5.13 | 32 | 7 | 5.095 | 58 | ||
| 94 | 93 | ||||||
| 9 | 16 | ||||||
| 4 | 5.12 | 30 | 8 | 5.09 | 59 | ||
| 92 | 93 |
For example, consider the Laplace double layer potential on the ‘starfish’ geometry (33) with the density function and the target point . Let be the near part of the boundary, on which adaptive QBX is applied. Depending on the partition of the boundary, position of with respect to can vary. We consider six different situations (see Fig. 5). Clearly, is fixed in all cases because is fixed, and it is always in front of the panel . In Table 2, we have shown values of the parameter at the end of [4, Algorithm 2] for some different tolerances . The midpoint of the preimage is shown in the row ‘midpoint’. It is seen that the smallest always corresponds with Fig. 4, in which the midpoint 5.12 is closest to .
2.3.2. Helmholtz potentials
For the Helmholtz single layer potential, the pair
| (41) |
with
| (42) |
is the -dependent factor of the coefficient .
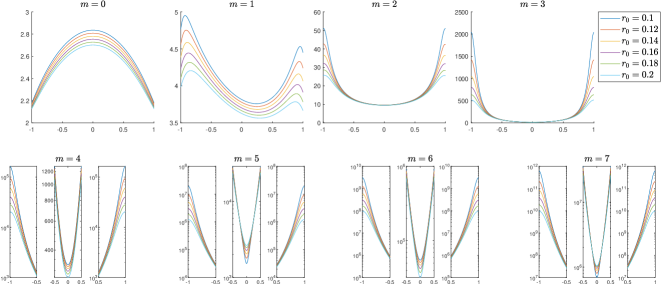
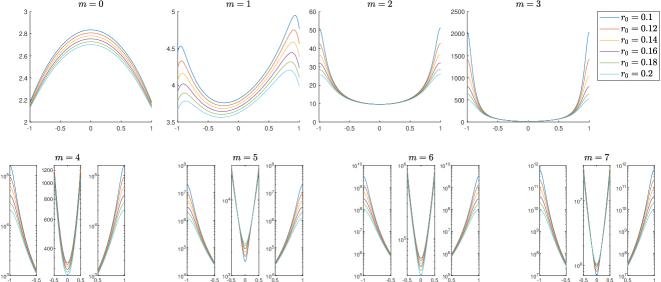
Clearly, both and satisfy (c2). Note that for any fixed , as grows. Thus, for the coefficient with larger , the condition (c1) holds approximately, i.e., , .
Here again our numerical experiments shows that is the minimizer of , for each , where
| (43) |
In Fig. 6 and Fig. 7, for fixed , , and some different values of , we have plotted and , respectively, as functions of . As it is seen, all the functions are minimized near when . As expected, the minimizer in each case approaches 0 as the index grows.
According to the above discussion, we recommend the following strategy for partitioning of the boundary with respect to the target point . Find the minimizer of . For a given small enough, let be the preimage of the near part, that means that adaptive QBX should be applied on , and a traditional quadrature rule should be employed on . It is recommended that is set to , where is the length of the near part (see [17]).
3. Algorithms
Assume that an approximation of the density is available for any in the panel . According to the comments in Section Section 2, one can consider the following algorithm as a revision to [4, Algorithms 1,2]:
| MAQBX. Modified adaptive QBX based on the Gauss-Legendre quadrature rules, when the panel resembles a straight segment, the target point lies in the bad annular neighborhood, and are known. |
|---|
| , |
| while do |
| end while |
| Apply the ()-point Gauss-Legendre rule to find . |
| repeat |
| while do |
| end while |
| Apply the ()-point Gauss-Legendre rule to find . |
| until |
| return and |
Thus, the main algorithm for computing the layer potential (9) on the whole boundary can be described by the following steps:
-
(1)
Find the minimizer of .
-
(2)
If is small enough, use the following steps; otherwise use a classical quadrature rule for computing the layer potential, and stop.
-
(3)
For a given small enough, set .
-
(4)
Set the half-width of the bad annular neighborhood of the boundary to , where is the length of , for .
-
(5)
Apply MAQBX to the near part , and
-
(6)
apply the Gauss-Legendre quadrature to the far part.
Remark 2.
In some cases, we can save some computational efforts in MAQBX. If the target point lies on the boundary, and the potential satisfies a jump condition, it is recommended that QBX should be applied with two expansion centers, say and , on the opposite sides of the boundary and the average of the two sided values is considered (see [17, §3.2]). Also for the Helmholtz potentials, one needs to evaluated both and for each positive . On the other hand, the following equalities hold due to and :
Hence, if we compute for some , we can immediately obtain , with no effort.
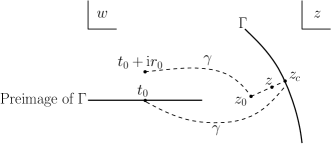
In BIM, the density function is unknown, but it can be approximated at any set of discrete points on the boundary . Divide the boundary into panels of an equal length . Let be a parametrization of for , and consider the roots of the Legendre polynomial of degree for some integer . The set of Gaussian points , , , on the boundary form the so-called underlying grid. In adaptive QBX (either the one proposed in this paper or in [4]) the density must be unsampled even to a finer grid. For this purpose, as proposed in [4], we use the Lagrange interpolation at the underlying grid. More precisely, for computing , where lies on the panel , we use the Lagrange interpolation of at . Note that in the main algorithm above, a near part may be different from all (see Fig. 8). However, the computational cost is not affected by whether the near part coincides with a panel of the underlying grid or not because the density should be resolved at finer grids anyway.
4. Numerical experiments
In this section, we carry out some numerical experiments by our desktop PC111Intel Core i7-7700 CPU with the clock speed of 3.60 GHz with 32 GB of RAM in order to illustrate efficiency of MAQBX.
4.1. Laplace layer potential evaluation
Consider the Laplace double layer potential on the ‘starfish’ geometry (33) with the density function . The exact value of the potential is for any target point in the interior domain. As target points, consider a grid of a small region near the boundary. In the main algorithm, we choose for each target point, resulting the near part to be always connected. For each target point, we apply MAQBX with to the near part, and the 256-point Gauss-Legendre rule to the far part of the boundary with the tolerances (see Fig. 9 for the absolute error).
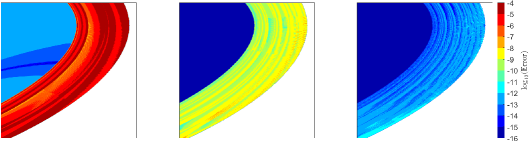
4.2. Comparison to AQBX
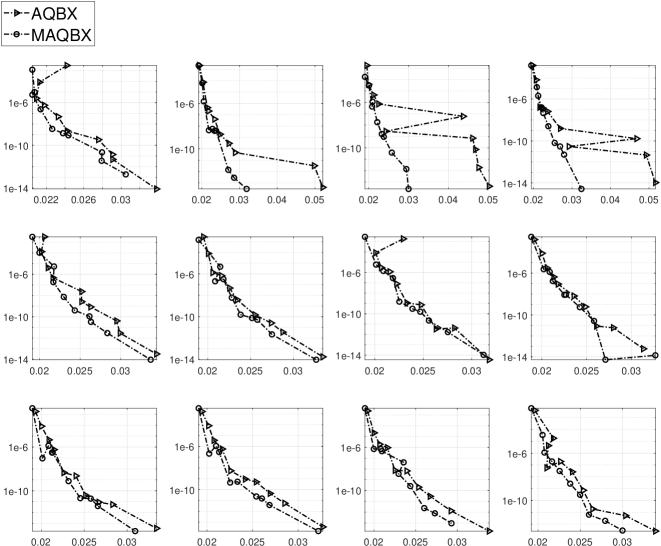
Here, we consider the CPU run-time consumed in implementation of the previous numerical experiment. For twelve target points, selected randomly close to the boundary (see Fig. 11), we implement adaptive QBX of [4] and Algorithms 1 and 2 proposed in this paper. We run each Matlab code 10 times and consider the average of the run-times. In Fig. 10, we compare performance of adaptive QBX with MAQBX. For each algorithm, we plot the relative error as a function of CPU run-time in seconds. As it is seen, MAQBX converges faster than adaptive QBX of [4] in general.
4.3. Solving a source point scattering problem
Before computing a layer potential, one should approximate the density function by solving the corresponding boundary integral equation. A more challenging task for adaptive QBX is thus in the context of solving boundary integral equations in which the target points lies on the boundary. In summary, we find a Nyström approximation of at an underlying grid on the boundary. Then, we use an accurate interpolation to approximate at a finer grid employed in adaptive QBX for computing the layer potential.
For the wave number , consider the Helmholtz exterior problem induced by six source points located in the interior of the ‘starfish’ geometry (33). We apply the boundary integral method with the combined field representation
| (44) |
where and are the Helmholtz single layer and double layer potentials, respectively. As the underlying grid, we divide the boundary into 50 panels of equal length and consider 16 Gauss-Legendre points in each panel. We apply the Nyström method to the corresponding boundary integral equation
| (45) |
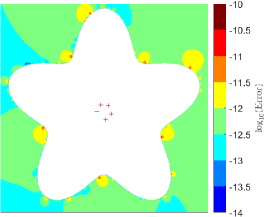
where is the Dirichlet data induced by the source points. Then, we use the Lagrange interpolation at the underlying grid to obtain an approximation of the density function. In order to solve the Nyström system, we use GMRES with the matrix-vector product carried out by MAQBX with and . The algorithms with the same parameters are then applied to compute the layer potential as the solution of the source-point problem (see Fig. 12 for the absolute errors). The near part for each target point is bounded in a parameter interval of length , and the 512-point Gauss-Legendre rule is applied to the far part.
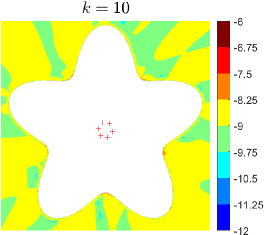
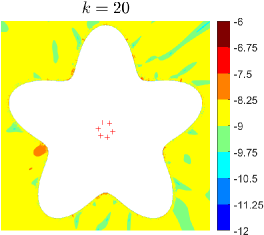
4.4. Higher wavenumbers
Here, we repeat the previous experiment, now for the higher wavenumbers and . The near part for each target point is bounded in a parameter interval of length . Other parameters of the algorithm remains the same as in Section 4.3. The results (Fig. 13) show that MAQBX is still practical for scattering problems with higher wavenumbers. The same observation has been reported in [4] for AQBX.
5. Conclusions
Adaptive QBX is a robust and accurate tool for computing layer potentials at target points near or on the boundary. In this paper, we have modified the main structure of Algorithms 1,2 of [4] in order to obviate the need to compute extra coefficients , which never appear in the truncated expansion of the potential. The modified AQBX is more rapid than AQBX of [4] in practice.
Acknowledgment
The author would like to thank Alex Barnett, Ludvig af Klinteberg, and Anna-Karin Tornberg for many valuable discussions.
References
- [1] (2022) Quadrature error estimates for layer potentials evaluated near curved surfaces in three dimensions. Comput. Math. Appl. 111, pp. 1–19. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [2] (2016) A fast integral equation method for solid particles in viscous flow using quadrature by expansion. J. Comput. Phys. 326, pp. 420–445. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [3] (2017) Error estimation for quadrature by expansion in layer potential evaluation. Adv. Comput. Math. 43, pp. 195–234. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [4] (2018) Adaptive quadrature by expansion for layer potential evaluation in two dimensions. SIAM J. Sci. Comput. 40, pp. 1225–1249. External Links: Link Cited by: Figure 10, §1.3, §1.4, §1.5, §1.5, §1, §1, §2.1, §2.1, §2.2, §2.2, §2.2, §2.3.1, Table 1, Table 2, §2, §3, §3, §4.2, §4.4, §5, Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗, Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗, Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗, Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [5] (1999) Hybrid Gauss-trapezoidal quadrature rules. SIAM J. Sci. Comput. 20, pp. 1551–1584. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [6] (2014) Evaluation of layer potentials close to the boundary for Laplace and Helmholtz problems on analytic planar domains. SIAM J. Sci. Comput. 36, pp. A427–A451. External Links: Link Cited by: §1.5, §1.5, Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [7] (2001) A method for computing nearly singular integrals. SIAM J. Numer. Anal. 38, pp. 1902–1925. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [8] (2010) A nonlinear optimization procedure for generalized Gaussian quadratures. SIAM J. Sci. Comput. 32, pp. 1761–1788. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [9] (2001) A fast, high-order algorithm for the solution of surface scattering problems: basic implementation, tests, and applications. J. Comput. Phys. 169, pp. 80–110. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [10] (2000) On the numerical solution of a hypersingular integral equation for elastic scattering from a planar crack. IMA J. Numer. Anal. 20, pp. 601–619. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [11] (1998) Inverse acoustic and electromagnetic scattering theory. 2nd edition, Springer-Verlag, Berlin. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [12] (2013) On the convergence of local expansions of layer potentials. SIAM J. Numer. Anal. 51, pp. 2660–2679. External Links: Link Cited by: §1, Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [13] (2008) Machine precision evaluation of singular and nearly singular potential integrals by use of Gauss quadrature formulas for rational functions. IEEE T. Antenn. Propag. 56 (4), pp. 981–998. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [14] (2008) On the evaluation of layer potentials close to their sources. J. Comput. Phys. 227, pp. 2899–2921. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [15] (2009) Integral equation methods for elliptic problems with boundary conditions of mixed type. J. Comput. Phys. 228, pp. 8892–8907. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [16] (1997) High-order corrected trapezoidal quadrature rules for singular functions. SIAM J. Numer. Anal. 34, pp. 1331–1356. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [17] (2013) Quadrature by expansion: A new method for the evaluation of layer potentials. J. Comput. Phys. 252, pp. 332–349. External Links: Link Cited by: §2.3.2, Remark 2, Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [18] (2001) Numerical quadratures for singular and hypersingular integrals. Comput. Math. Appl. 41, pp. 327–352. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [19] (2023) Digital library of mathematical functions. Release 1.1.12. External Links: Link Cited by: §1.3.
- [20] (2017) Fast algorithms for quadrature by expansion I: globally valid expansions. J. Comput. Phys. 345, pp. 706–731. External Links: Link Cited by: §1.5, Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [21] (2018) Ubiquitous evaluation of layer potentials using quadrature by kernel-independent expansion. BIT Numer. Math. 58, pp. 423–456. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [22] (1992) On numerical cubatures of singular surface integrals in boundary element methods. Numer. Math. 62, pp. 343–369. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [23] (2018) A local target specific quadrature by expansion method for evaluation of layer potentials in 3D. J. Comput. Phys. 364, pp. 365–392. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [24] (2023) Estimation of quadrature errors for layer potentials evaluated near surfaces with spherical topology. Adv. Comput. Math. 49, pp. 87. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [25] (2018) A fast algorithm with error bounds for quadrature by expansion. J. Comput. Phys. 374, pp. 135–162. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [26] (2019) A fast algorithm for quadrature by expansion in three dimensions. J. Comput. Phys. 388, pp. 655–689. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.
- [27] (2020) Optimization of fast algorithms for global quadrature by expansion using target-specific expansions. J. Comput. Phys. 403, pp. 108976. External Links: Link Cited by: Modified adaptive quadrature by expansion for Laplace and Helmholtz layer potentials in 2D∗.










