La détermination «in situ» de quelques grandeurs thermiques des calcaires

Nicolae Suciu
(original), html, Numerical Modeling, paper

Abstract

 

Authors

N. Suciu

Keywords

References

PDF

https://ictp.acad.ro/wp-content/uploads/2025/10/1981-Suciu-La-determination-in-situ-de-quelques-grandeurs-thermiques-des-calcaires-1.pdf

About this paper

Cite this paper as:
N. Suciu (1981), La détermination «in situ» de quelques grandeurs thermiques des calcaires, Trav. Inst Spéol. «Emile Racovitza», vol. XX, 179-185
Journal

Trav. Inst Spéol. «Emile Racovitza»

Publisher Name
DOI

Not available yet.

Print ISSN

Not available yet.

Online ISSN

Not available yet.

Google Scholar Profile

Paper in HTML form

1981 Suciu - La determination-in situ- de quelques grandeurs thermiques des calcaires

La détermination "in situ" de quelques grandeurs thermiques des calcaires

par

N. Suciu

On présente une détermination «in situ» de quelques grandeurs thermiques des calcaires. On a déterminé des grandeurs globales et des moyennes annuelles caractéristiques à la couche calcaire lapiézée sous laquelle se trouve la grotte-aven «Cioaca cu brebenei », du massif Piatra Mare-Cloșani. A l'aide d'un modèle simplifié de la couche calcaire, on a exprimé la dépendance entre les propriétés thermiques des calcaires due à la fissuration et la quantité moyenne annuelle d'eau dans la couche.

1. Introduction

On a mesuré la température de la roche à diverses profondeurs dans la couche ( 30 cm , 75 cm 30 cm , 75 cm 30cm,75cm30 \mathrm{~cm}, 75 \mathrm{~cm}30 cm,75 cm et 117 cm ), ainsi qu'en divers points de la grotte (en air et à 5 cm dans les parois), pendant l'intervalle juillet 1979 - juillet 1980. On a utilisé des thermomètres à mercure et un thermomètre à thermistance (fig. 1).
En même temps on a déterminé dans le laboratoire, la conductivité thermique ( K ) ( K ) (K)(K)(K) et la capacité calorique de l'unité de volume ( ρ c ρ c rho c\rho cρc ) pour trois sets d'échantillons provenant respectivement du lapiaz de l'extérieur, du plafond de la grotte et d'un fragment de stalactite. La conductivité thermique a été déterminée dans le Laboratoire des champs naturels du Centre de la physique de la terre et de séismologie - Bucarest », par la méthode de l'appareil aux barres (C. Demetrescu, 1977). La capacité calorique a été déterminée dans le Laboratoire de physique moléculaire de la «Faculté de physique - Bucarest», par la méthode calorimétrique.

2. Résumé théorique de la méthode

L'équation de la propagation de la chaleur dans un milieu solide, homogène et isotrope, ayant la conductivité thermique K K KKK, la densité p p ppp et la chaleur spécifique c c ccc, est (Cars low and Jaege r, 1957) :
∇ 2 T − 1 x ∂ T ∂ t = 0 , où x = K ρ c ∇ 2 T − 1 x ∂ T ∂ t = 0 ,  où  x = K ρ c grad^(2)T-(1)/(x)(del T)/(del t)=0," où "x=(K)/(rho c)\nabla^{2} T-\frac{1}{x} \frac{\partial T}{\partial t}=0, \text { où } x=\frac{K}{\rho c}∇2T−1x∂T∂t=0, où x=Kρc
est la diffusivité thermique, T − T − T-T-T− la température et t − t − t-t-t− le temps. Dans le cas unidimensionnel, pour un solide semi-infini ( x ⩾ 0 x ⩾ 0 x >= 0x \geqslant 0x⩾0 ) l'équation devient:
∂ 2 T ∂ x 2 − 1 ϰ ∂ T ∂ t = 0 ∂ 2 T ∂ x 2 − 1 ϰ ∂ T ∂ t = 0 (del^(2)(T))/(delx^(2))-(1)/(ϰ)(del(T))/(delt)=0\frac{\partial^{2} \mathrm{~T}}{\partial \mathrm{x}^{2}}-\frac{1}{\varkappa} \frac{\partial \mathrm{~T}}{\partial \mathrm{t}}=0∂2 T∂x2−1ϰ∂ T∂t=0
Trav. Inst. Spéol. «Emile Racovitza», t. XX, p. 179-185, Bucarest, 1981
Si à la surface du solide il y a une oscillation de température :
T ( 0 , t ) = A cos ⁡ ( ω t − ε ) T ( 0 , t ) = A cos ⁡ ( ω t − ε ) T(0,t)=A cos(omega t-epsi)T(0, t)=A \cos (\omega t-\varepsilon)T(0,t)=Acos⁡(ωt−ε)
la solution finit quand t → ∞ t → ∞ t rarr oot \rightarrow \inftyt→∞ est :
T ( x , t ) = A e − k x cos ⁡ ( ω t − k x − ε ) ; k = ω / 2 x = π / τ x T ( x , t ) = A e − k x cos ⁡ ( ω t − k x − ε ) ; k = ω / 2 x = π / τ x T(x,t)=Ae^(-kx)cos(omega t-kx-epsi);k=sqrt(omega//2x)=sqrt(pi//tau x)T(x, t)=A e^{-k x} \cos (\omega t-k x-\varepsilon) ; k=\sqrt{\omega / 2 x}=\sqrt{\pi / \tau x}T(x,t)=Ae−kxcos⁡(ωt−kx−ε);k=ω/2x=π/τx
où τ τ tau\tauτ représente la période de l'oscillation.
Donc, la solution est une onde de température ayant le nombre d'onde k k kkk et la longueur d'onde λ = 2 π / k λ = 2 π / k lambda=2pi//k\lambda=2 \pi / \mathrm{k}λ=2π/k.

a) Détermination du nombre d'onde

On détermine k k kkk à l'aide de la relation qui donne l'amplitude de l'onde de température:
a = A e − kx a = A e − kx a=Ae^(-kx)\mathrm{a}=\mathrm{A} \mathrm{e}^{-\mathrm{kx}}a=Ae−kx
Il faut remarquer ici qu'en vertu de cette relation, lorsque la température superficielle est exprimée par une série Fourier, les harmoniques supérieures disparaissent plus vite que les harmoniques inférieures, c'est-àdire, ce ne sont que les ondes de grandes périodes qui atteignent les grandes profondeurs; c'est le cas de la couche calcaire de «Cioaca cu brebenei», où l'onde annuelle seule pénètre dans la grotte (l'épaisseur de la couche x = L = 800 cm x = L = 800 cm x=L=800cmx=L=800 \mathrm{~cm}x=L=800 cm ). Dans les points de mesurage de l'extérieur, les harmoniques supérieures sont éliminées par les moyennes mensuelles 1 1 ^(1){ }^{1}1.
Considérant les amplitudes dans le point x = L x = L x=Lx=Lx=L et en d'autres points x ≠ L x ≠ L x!=Lx \neq Lx≠L on obtient :
(1) k = ln ⁡ a x a L L − x (1) k = ln ⁡ a x a L L − x {:(1)k=(ln((a_(x))/(a_(L))))/((L)-x):}\begin{equation*} \mathrm{k}=\frac{\ln \frac{\mathrm{a}_{\mathrm{x}}}{\mathrm{a}_{\mathrm{L}}}}{\mathrm{~L}-\mathrm{x}} \tag{1} \end{equation*}(1)k=ln⁡axaL L−x
b) Le modèle de couche composé pour la couche réelle et la détermination de la conductivité thermique et de la capacité calorique globales et moyennes annuelles
Pour exprimer les grandeurs K K KKK et ρ c ρ c rho c\rho cρc qui interviennent en k k kkk, il faut connaître la manière de propagation de l'onde thermique à travers la couche réelle, composée de calcaires compacts et de fissures, partiellement libres, partiellement remplies d'eau.
Avant de choisir le modèle on fait les observations suivantes :
  • au point de vue morphologique la couche est un lapiaz; les fissures verticales sont prédominantes par rapport à celles transversales développées selon la direction de la stratification (fig. 1);
  • en tenant compte de l'épaisseur réduite de la couche considérée, l'existence d'une cavité de grandes dimensions est peu probable et la plus
température :
ω / 2 x = π / τ x ω / 2 x = π / τ x sqrt(omega//2x)=sqrt(pi//tau x)\sqrt{\omega / 2 x}=\sqrt{\pi / \tau x}ω/2x=π/τx
rant le nombre d'onde k k kkk i donne l'amplitude de relation, lorsque la temFourier, les harmoniques iques inférieures, c'est-àui atteignent les grandes de «Cioaca cu brebenei», l'épaisseur de la couche le l'extérieur, les harmomes mensuelles 1 1 ^(1){ }^{1}1.
= L = L =L=L=L et en d'autres points
couche réelle et la déterpacité calorique globales
aterviennent en k k kkk, il faut thermique à travers la et de fissures, partielle-
rvations suivantes:
uche est un lapiaz; les rt à celles transversales n (fig. 1);
de la couche considérée, st peu probable et la plus
es mensuelles tiennent compte
simple hypothèse sur la distribution des fissures est celle d'une distribution homogène ;
  • dû à la communication des fissures normales avec les joints de stratifications, l'eau remplit les fissures au même niveau ;
de la couche calcaire.
  • on peut démontrer que la température de l'air dans une fissure ouverte tend exponentiellement vers la température des parois ( C i g n a , 1960). Le même phénomène a lieu dans le cas où la fissure est pleine d'eau. En même temps, l'intervalle où s'établit l'équilibre thermique entre l'air, respectivement l'eau de la fissure, et ses parois est très petit rapport à la période de l'oscillation annuelle de température.
Tenant compte de ces observations, on propose un modèle où la couche est équivalente à un système de trois conducteurs thermiques: l'un de longueur L L LLL et surface S c S c S_(c)S_{c}Sc de calcaires compacts, en parallèle avec deux autres conducteurs ensériés ayant les longueurs L − 1 L − 1 L-1L-1L−1 et 1 et la surface S a S a S_(a)S_{a}Sa de l'air, respectivement de l'eau (fig. 2).
Les paramètres de structure de cette couche sont : la fissuration F = S a / S F = S a / S F=S_(a)//SF=S_{a} / SF=Sa/S (où S = S a + S c S = S a + S c S=S_(a)+S_(c)S=S_{a}+S_{c}S=Sa+Sc ) et le rapport de remplissage d'eau des fissures : p = 1 L p = 1 L p=(1)/(L)p=\frac{1}{L}p=1L.
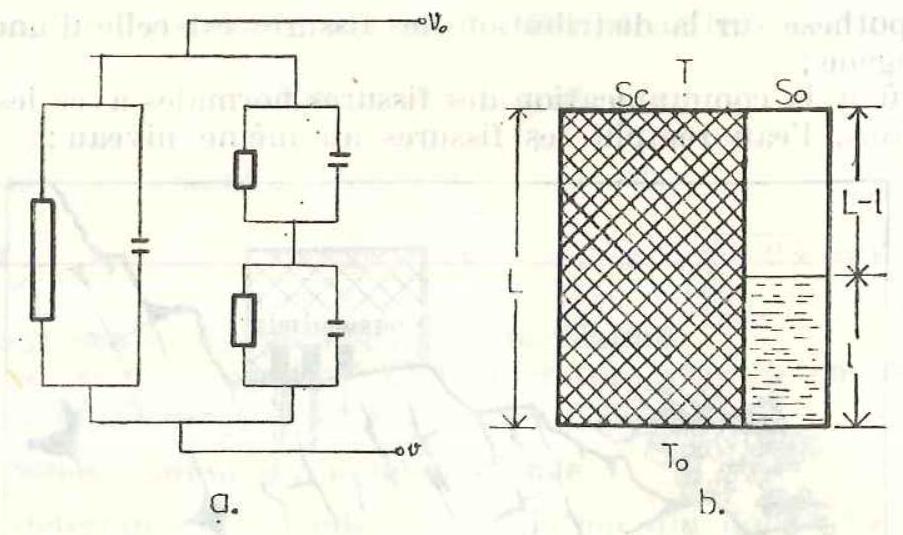
On résoud le problème du flux thermique par analogie à celui de la propagation de la charge électrique par un conducteur à résistance et capacité. Pour respecter l'analogie on pose la condition que la grandeur K K KKK qui intervient en k k kkk représente la conductivité thermique équivalente de la couche en régime stationnaire.
Fig. 2. - Modèle simplifié de la couche calcaire et le circuit électrique équivalent.
Avec les notations :
k , K , ρ c - pour la couche k 1 , K 1 , ( ρ c ) 1 - pour le calcaire compact k 2 , K 2 , ( ρ c ) 2 - pour l'air k 3 , K 3 , ( ρ c ) 3 - pour l'eau k , K , ρ c  - pour la couche  k 1 , K 1 , ( ρ c ) 1  - pour le calcaire compact  k 2 , K 2 , ( ρ c ) 2  - pour l'air  k 3 , K 3 , ( ρ c ) 3  - pour l'eau  {:[k","K","rhoc" - pour la couche "],[k_(1)","K_(1)","(rhoc)_(1)" - pour le calcaire compact "],[k_(2)","K_(2)","(rhoc)_(2)" - pour l'air "],[k_(3)","K_(3)","(rhoc)_(3)" - pour l'eau "]:}\begin{aligned} & \mathrm{k}, \mathrm{~K}, \rho \mathrm{c} \text { - pour la couche } \\ & \mathrm{k}_{1}, \mathrm{~K}_{1},(\rho \mathrm{c})_{1} \text { - pour le calcaire compact } \\ & \mathrm{k}_{2}, \mathrm{~K}_{2},(\rho \mathrm{c})_{2} \text { - pour l'air } \\ & \mathrm{k}_{3}, \mathrm{~K}_{3},(\rho \mathrm{c})_{3} \text { - pour l'eau } \end{aligned}k, K,ρc - pour la couche k1, K1,(ρc)1 - pour le calcaire compact k2, K2,(ρc)2 - pour l'air k3, K3,(ρc)3 - pour l'eau 
on obtient:
(2)
K = ( 1 − F ) K 1 + F K 2 K 3 ( 1 − p ) K 3 + p K 2 ρ c = τ k 2 K π K = ( 1 − F ) K 1 + F K 2 K 3 ( 1 − p ) K 3 + p K 2 ρ c = τ k 2 K π {:[K=(1-F)K_(1)+F(K_(2)K_(3))/((1-p)K_(3)+pK_(2))],[rhoc=(tauk^(2)K)/(pi)]:}\begin{gathered} \mathbf{K}=(1-\mathbf{F}) \mathbf{K}_{1}+\mathbf{F} \frac{\mathbf{K}_{2} \mathbf{K}_{3}}{(1-\mathbf{p}) \mathbf{K}_{3}+\mathbf{p} \mathbf{K}_{2}} \\ \rho \mathbf{c}=\frac{\tau \mathbf{k}^{2} \mathbf{K}}{\pi} \end{gathered}K=(1−F)K1+FK2K3(1−p)K3+pK2ρc=τk2Kπ
(3)
La fissuration a été déterminée pour p = 1 p = 1 p=1\mathrm{p}=1p=1 (au mois d'avril 1980, après la fonte des neiges), à l'aide d'une valeur k déterminée approximativement par la méthode des différences finies, avec la relation:
(4) F = K 1 ( k − k 1 ) K 1 ( k − k 1 ) + K 3 ( k 3 − k ) (4) F = K 1 k − k 1 K 1 k − k 1 + K 3 k 3 − k {:(4)F=(K_(1)(k-k_(1)))/(K_(1)(k-k_(1))+K_(3)(k_(3)-k)):}\begin{equation*} \mathrm{F}=\frac{\mathrm{K}_{1}\left(\mathrm{k}-\mathrm{k}_{1}\right)}{\mathrm{K}_{1}\left(\mathrm{k}-\mathrm{k}_{1}\right)+\mathrm{K}_{3}\left(\mathrm{k}_{3}-\mathrm{k}\right)} \tag{4} \end{equation*}(4)F=K1(k−k1)K1(k−k1)+K3(k3−k)
On obtient le rapport moyen de remplissage avec de l'eau par la substitution de K K KKK et F ′ F ′ F^(')F^{\prime}F′ dans :
(5) kK = ( 1 − F ) k 1 K 1 + F k 2 k 3 K 2 K 3 p k 2 K 2 + ( 1 − p ) k 3 K 3 (5) kK = ( 1 − F ) k 1 K 1 + F k 2 k 3 K 2 K 3 p k 2 K 2 + ( 1 − p ) k 3 K 3 {:(5)kK=(1-F)k_(1)K_(1)+F(k_(2)k_(3)K_(2)K_(3))/(pk_(2)K_(2)+(1-p)k_(3)K_(3)):}\begin{equation*} \mathrm{kK}=(1-\mathrm{F}) \mathrm{k}_{1} \mathrm{~K}_{1}+\mathrm{F} \frac{\mathrm{k}_{2} \mathrm{k}_{3} \mathrm{~K}_{2} \mathrm{~K}_{3}}{p \mathrm{k}_{2} \mathrm{~K}_{2}+(1-\mathrm{p}) \mathrm{k}_{3} \mathrm{~K}_{3}} \tag{5} \end{equation*}(5)kK=(1−F)k1 K1+Fk2k3 K2 K3pk2 K2+(1−p)k3 K3
(au mois d'avril 1980, déterminée approximavec la relation :
k) ―  k)  ¯ bar(" k) ")\overline{\text { k) }} k) ―
e avec de l'eau par la
K 2 K 3 K 2 K 3 K_(2)K_(3)\mathrm{K}_{2} \mathrm{~K}_{3}K2 K3
1 − p ) k 3 K 3 1 − p ) k 3 K 3 1-p)k_(3)K_(3)1-p) \mathrm{k}_{3} \mathrm{~K}_{3}1−p)k3 K3
e) L'anisotropie thermique des calcaires compacts
La conductivité thermique des calcaires compacts dépend de la direction du flux thermique par rapport à la normale du plan de sédimentation.
Les échantillons mesurés présentent deux conductivités principales correspondant au plan de stratification et à la normale de celui-là :
K a et K c ( K a > K c ) . K a  et  K c K a > K c . K_(a)" et "K_(c)(K_(a) > K_(c)).\mathrm{K}_{a} \text { et } \mathrm{K}_{c}\left(\mathrm{~K}_{a}>\mathrm{K}_{c}\right) .Ka et Kc( Ka>Kc).
Pour une direction quelconque θ θ theta\thetaθ, la conductivité est donnée par:
(6) K θ = K α + ( K c − K a ) cos 2 ⁡ θ (6) K θ = K α + K c − K a cos 2 ⁡ θ {:(6)K_(theta)=K_(alpha)+(K_(c)-K_(a))cos^(2)theta:}\begin{equation*} \mathbf{K}_{\theta}=\mathbf{K}_{\alpha}+\left(\mathbf{K}_{c}-\mathbf{K}_{a}\right) \cos ^{2} \theta \tag{6} \end{equation*}(6)Kθ=Kα+(Kc−Ka)cos2⁡θ
Dans le cas des échantillons de «Cioaca cu brebenei », l'angle d'inclinaison par rapport à la verticale (la direction de propagation du flux thermique) du plan de sédimentation est approximativement l'angle d'entre la verticale et le plan de stratification ( θ = 30 ∘ ) θ = 30 ∘ (theta=30^(@))\left(\theta=30^{\circ}\right)(θ=30∘). Pour que la valeur de K employée en (2), (4) et (5) fût représentative pour la couche, on considère la moyenne entre les valeurs de l'extérieur et celles de l'intérieur.

3. Les résultats obtenus

a) Les résultats des mesurages de laboratoire sont marqués dans le tableau 1.
Tableau 1
Extérieur Intéricur Stalactite
K a ( cal cm s ∘ C ) K a cal cm s ∘ C K_(a)((cal)/(cms^(@)C))\mathrm{K}_{\mathrm{a}}\left(\frac{\mathrm{cal}}{\mathrm{cm} \mathrm{s}{ }^{\circ} \mathrm{C}}\right)Ka(calcms∘C) 0 , 00210 ± 0 , 00002 0 , 00210 ± 0 , 00002 0,00210+-0,000020,00210 \pm 0,000020,00210±0,00002 0 , 00709 ± 0 , 00002 0 , 00709 ± 0 , 00002 0,00709+-0,000020,00709 \pm 0,000020,00709±0,00002 0 , 00703 ± 0 , 00002 0 , 00703 ± 0 , 00002 0,00703+-0,000020,00703 \pm 0,000020,00703±0,00002
K c ( cal cm s ∘ C ) K c cal cm s ∘ C K_(c)((cal)/(cms^(@)C))\mathrm{K}_{\mathrm{c}}\left(\frac{\mathrm{cal}}{\mathrm{cm} \mathrm{s}{ }^{\circ} \mathrm{C}}\right)Kc(calcms∘C) 0 , 00134 ± 0 , 00002 0 , 00134 ± 0 , 00002 0,00134+-0,000020,00134 \pm 0,000020,00134±0,00002 0 , 00448 ± 0 , 00002 0 , 00448 ± 0 , 00002 0,00448+-0,000020,00448 \pm 0,000020,00448±0,00002
ρ c ( c a l cm 3 C ) ρ c c a l cm 3 C rho c((cal)/(cm^(3)C))\rho c\left(\frac{c a l}{\mathrm{~cm}^{3} \mathrm{C}}\right)ρc(cal cm3C) 0 , 66 ± 0 , 02 0 , 66 ± 0 , 02 0,66+-0,020,66 \pm 0,020,66±0,02 0 , 66 ± 0 , 02 0 , 66 ± 0 , 02 0,66+-0,020,66 \pm 0,020,66±0,02 0 , 53 ± 0 , 02 0 , 53 ± 0 , 02 0,53+-0,020,53 \pm 0,020,53±0,02
Extérieur Intéricur Stalactite K_(a)((cal)/(cms^(@)C)) 0,00210+-0,00002 0,00709+-0,00002 0,00703+-0,00002 K_(c)((cal)/(cms^(@)C)) 0,00134+-0,00002 0,00448+-0,00002 rho c((cal)/(cm^(3)C)) 0,66+-0,02 0,66+-0,02 0,53+-0,02| | Extérieur | Intéricur | Stalactite | | :--- | :--- | :--- | :--- | | $\mathrm{K}_{\mathrm{a}}\left(\frac{\mathrm{cal}}{\mathrm{cm} \mathrm{s}{ }^{\circ} \mathrm{C}}\right)$ | $0,00210 \pm 0,00002$ | $0,00709 \pm 0,00002$ | $0,00703 \pm 0,00002$ | | $\mathrm{K}_{\mathrm{c}}\left(\frac{\mathrm{cal}}{\mathrm{cm} \mathrm{s}{ }^{\circ} \mathrm{C}}\right)$ | $0,00134 \pm 0,00002$ | $0,00448 \pm 0,00002$ | | | $\rho c\left(\frac{c a l}{\mathrm{~cm}^{3} \mathrm{C}}\right)$ | $0,66 \pm 0,02$ | $0,66 \pm 0,02$ | $0,53 \pm 0,02$ |
Pour θ = 30 ∘ θ = 30 ∘ theta=30^(@)\theta=30^{\circ}θ=30∘ on a obtenu K 1 K 1 K_(1)K_{1}K1 à l'aide de la relation (6) :
K 1 = K ( 30 ∘ ) = ( 0 , 0040 ± 0 , 00002 ) cal cm s ∘ C K 1 = K 30 ∘ = ( 0 , 0040 ± 0 , 00002 ) cal cm s ∘ C K_(1)=K(30^(@))=(0,0040+-0,00002)(cal)/((cm)s^(@)C)\mathrm{K}_{1}=\mathrm{K}\left(30^{\circ}\right)=(0,0040 \pm 0,00002) \frac{\mathrm{cal}}{\mathrm{~cm} \mathrm{~s}^{\circ} \mathrm{C}}K1=K(30∘)=(0,0040±0,00002)cal cm s∘C
et le nombre d'onde:
k 1 = ( 0 , 0041 ± 0 , 00004 ) cm − 1 k 1 = ( 0 , 0041 ± 0 , 00004 ) cm − 1 k_(1)=(0,0041+-0,00004)cm^(-1)\mathrm{k}_{1}=(0,0041 \pm 0,00004) \mathrm{cm}^{-1}k1=(0,0041±0,00004)cm−1
b) En appliquant la relation (1) pour : x = 30 cm , 75 cm x = 30 cm , 75 cm x=30cm,75cm\mathrm{x}=30 \mathrm{~cm}, 75 \mathrm{~cm}x=30 cm,75 cm et 117 cm et pour L = 800 cm L = 800 cm L=800cm\mathrm{L}=800 \mathrm{~cm}L=800 cm, on a obtenu la valeur moyenne pour k :
k = ( 0 , 0044 ± 0 , 0001 ) cm − 1 k = ( 0 , 0044 ± 0 , 0001 ) cm − 1 k=(0,0044+-0,0001)cm^(-1)\mathrm{k}=(0,0044 \pm 0,0001) \mathrm{cm}^{-1}k=(0,0044±0,0001)cm−1
À l'aide des relations (2) et (3) on a obtenu:
K = ( 0 , 0032 ± 0 , 0006 ) cal cm s ∘ C ρ c = ( 0 , 62 ± 0 , 07 ) cal cm 3 C K = ( 0 , 0032 ± 0 , 0006 ) cal cm s ∘ C ρ c = ( 0 , 62 ± 0 , 07 ) cal cm 3 C {:[K=(0","0032+-0","0006)(cal)/((cm)(s)^(@)C)],[rhoc=(0","62+-0","07)(cal)/(cm^(3)C)]:}\begin{aligned} \mathrm{K} & =(0,0032 \pm 0,0006) \frac{\mathrm{cal}}{\mathrm{~cm} \mathrm{~s}{ }^{\circ} \mathrm{C}} \\ \rho \mathrm{c} & =(0,62 \pm 0,07) \frac{\mathrm{cal}}{\mathrm{~cm}^{3} \mathrm{C}} \end{aligned}K=(0,0032±0,0006)cal cm s∘Cρc=(0,62±0,07)cal cm3C
Pour comparer, on ajoute le tableau 2 :
Tablean 2
le milieu 2 2 ^(2){ }^{2}2 P e ( cal cm 3 ∘ C ) P e cal cm 3 ∘ C P_(e)((cal)/(cm^(3)^(@)C))\mathrm{P}_{\mathrm{e}}\left(\frac{\mathrm{cal}}{\mathrm{cm}^{3}{ }^{\circ} \mathrm{C}}\right)Pe(calcm3∘C) K ( cal cm s ∘ C ) K cal cm s ∘ C K((cal)/(cms^(@)C))\mathrm{K}\left(\frac{\mathrm{cal}}{\mathrm{cm} \mathrm{s}{ }^{\circ} \mathrm{C}}\right)K(calcms∘C)
calcaires compacts 0,66 0,0040
couche de calcaires 0,62 0,0032
granit 0,54 0,0060
valeur moyenne pour des roches - 0,0042
air 0,0003 0,000058
eau 1,0 0,0014
Tablean 2 le milieu ^(2) P_(e)((cal)/(cm^(3)^(@)C)) K((cal)/(cms^(@)C)) calcaires compacts 0,66 0,0040 couche de calcaires 0,62 0,0032 granit 0,54 0,0060 valeur moyenne pour des roches - 0,0042 air 0,0003 0,000058 eau 1,0 0,0014| Tablean 2 | | | | :--- | :--- | :--- | | le milieu ${ }^{2}$ | $\mathrm{P}_{\mathrm{e}}\left(\frac{\mathrm{cal}}{\mathrm{cm}^{3}{ }^{\circ} \mathrm{C}}\right)$ | $\mathrm{K}\left(\frac{\mathrm{cal}}{\mathrm{cm} \mathrm{s}{ }^{\circ} \mathrm{C}}\right)$ | | calcaires compacts | 0,66 | 0,0040 | | couche de calcaires | 0,62 | 0,0032 | | granit | 0,54 | 0,0060 | | valeur moyenne pour des roches | - | 0,0042 | | air | 0,0003 | 0,000058 | | eau | 1,0 | 0,0014 |
On a déterminé F F F\mathbf{F}F et p p p\mathbf{p}p des relations (4) et (5). Dans la relation (4) on a employé la valeur k = ( 0 , 0045 ± 0 , 001 ) cm − 1 k = ( 0 , 0045 ± 0 , 001 ) cm − 1 k=(0,0045+-0,001)cm^(-1)\mathrm{k}=(0,0045 \pm 0,001) \mathrm{cm}^{-1}k=(0,0045±0,001)cm−1, déterminée par la méthode des différences finies, à l'aide des mesurages d'avril 1980 dans les points: x = 30 cm , 75 cm , 117 cm x = 30 cm , 75 cm , 117 cm x=30cm,75cm,117cm\mathrm{x}=30 \mathrm{~cm}, 75 \mathrm{~cm}, 117 \mathrm{~cm}x=30 cm,75 cm,117 cm, et les points supplémentaires: x = 5 cm x = 5 cm x=5cm\mathrm{x}=5 \mathrm{~cm}x=5 cm, 10 cm , 139 cm , 157 cm 10 cm , 139 cm , 157 cm 10cm,139cm,157cm10 \mathrm{~cm}, 139 \mathrm{~cm}, 157 \mathrm{~cm}10 cm,139 cm,157 cm.
On a obtenu :
F = ( 0 , 21 ± 0 , 06 ) ou F = ( 21 ± 6 ) % p = ( 0 , 42 ± 0 , 20 ) ou p = ( 42 ± 20 ) % F = ( 0 , 21 ± 0 , 06 )  ou  F = ( 21 ± 6 ) % p = ( 0 , 42 ± 0 , 20 )  ou  p = ( 42 ± 20 ) % {:[F=(0","21+-0","06)" ou "F=(21+-6)%],[p=(0","42+-0","20)" ou "p=(42+-20)%]:}\begin{aligned} & \mathrm{F}=(0,21 \pm 0,06) \text { ou } \mathrm{F}=(21 \pm 6) \% \\ & \mathrm{p}=(0,42 \pm 0,20) \text { ou } \mathrm{p}=(42 \pm 20) \% \end{aligned}F=(0,21±0,06) ou F=(21±6)%p=(0,42±0,20) ou p=(42±20)%

4. Conclusions

  • Les calcaires compacts sont anisotropes de point de vue thermique. Il y a une conductivité maximale dans' le plan de sédimentation et une conductivité minimale dans la direction perpendiculaire à celui-ci.
  • Les propriétés thermiques des calcaires dépendent de la structure de la fissuration autant que du poids des fissures et de leur teneur en eau.
0 cm , 75 cm 0 cm , 75 cm 0cm,75cm0 \mathrm{~cm}, 75 \mathrm{~cm}0 cm,75 cm et 117 cm me pour k:
u:
∘ C ∘ C ^(@)C{ }^{\circ} \mathrm{C}∘C
) K ( cal cm s ∘ C ) K cal cm s ∘ C K((cal)/(cms^(@)C))\mathrm{K}\left(\frac{\mathrm{cal}}{\mathrm{cm} \mathrm{s}{ }^{\circ} \mathrm{C}}\right)K(calcms∘C)
0,0040
0,0032
0,0060
0,0042
0,000058
0,0014
0,0040 0,0032 0,0060 0,0042 0,000058 0,0014| 0,0040 | | :--- | | 0,0032 | | 0,0060 | | 0,0042 | | 0,000058 | | 0,0014 |
u: ^(@)C ) K((cal)/(cms^(@)C)) "0,0040 0,0032 0,0060 0,0042 0,000058 0,0014"| u: | | | :--- | :--- | | ${ }^{\circ} \mathrm{C}$ | | | ) | $\mathrm{K}\left(\frac{\mathrm{cal}}{\mathrm{cm} \mathrm{s}{ }^{\circ} \mathrm{C}}\right)$ | | | 0,0040 <br> 0,0032 <br> 0,0060 <br> 0,0042 <br> 0,000058 <br> 0,0014 |
5). Dans la relation (4) n − 1 n − 1 n^(-1)\mathrm{n}^{-1}n−1, déterminée par la ges d'avril 1980 dans les plémentaires: x = 5 cm x = 5 cm x=5cm\mathrm{x}=5 \mathrm{~cm}x=5 cm,
6)%
20 ) % 20 ) % 20)%20) \%20)%
de point de vue thermian de sédimentation et pendiculaire à celui-ci. épendent de la structure et de leur teneur en eau.
nd Jaeger, 1957.
  • De p et F on obtient le volume moyen de l'eau contenu dans la couche : V = p . F . L . S V = p . F . L . S V=p.F.L.S\mathrm{V}=\mathrm{p} . \mathrm{F} . \mathrm{L} . \mathrm{S}V=p.F.L.S, et la colonne d'eau correspondante : l ′ = V / S l ′ = V / S l^(')=V//S\mathrm{l}^{\prime}=\mathrm{V} / \mathrm{S}l′=V/S. On obtient: l ′ = 665 , 6 mm l ′ = 665 , 6 mm l^(')=665,6mm\mathrm{l}^{\prime}=665,6 \mathrm{~mm}l′=665,6 mm (la somme annuelle des précipitations à la Station météorologique Cloşani de l'Institut de Spéologie est de 970 mm ). La couche a donc une capacité de rétention remarquable.
  • La température de l'air a une évolution semblable à celle de la température des parois, excepté les points de la zone vestibulaire de la grotte. C'est-à-dire que les amplitudes thermiques sont amortisées en profondeur et le maximum de température est retardé par rapport à celui de l'extérieur. Le flux thermique transmis par la couche de calcaires est done un facteur spéléoclimatique.

Bibliographie

1960 CiGNA, A., Air Temperature Distribution near the Entrance of Caves. Atti del Symposium Internationale di Speleologia, Villa Monastero, Varena.
1976 BLEAHU, M., DECU, V et colab., Peșteri din România. Editura științifică și enciclopedică, Bucureşti.
1957 CARSLOW, II. S. and JAEGER, J. C., Conduction of Heat in Solids. Oxford at the Clarendon Press.
1977 DEMETRESCU, C., Contribuļii la studiul fluxului termic al pămintului in Transilvania, thèse de doctorat (Manuscrit), Univ. București, Faculté de Physique.
1968 HUTT and BERG, Thermal and Electrical Conductivities of sandslone Rocks and Sediments, Geophysics, 33, 3, 489-500.
Institut de Spéologie «Emile Racovitza* Bucarest
Reçu le 28 Janvier 1981
  1. 1 1 ^(1){ }^{1}1 L'amélioration de la précision exige que les moyennes mensuelles tiennent compte des données de plusieurs années.
  2. 2 2 ^(2){ }^{2}2 Les quatre dernières valeurs proviennent de Carslow and Jaeger, 1957.
1981

Related Posts