Stable spectral collocation solutions to Cauchy problems for nonlinear dispersive wave equations

Călin-Ioan Gheorghiu
(proceedings), paper

Abstract

In this paper we are concerned with accurate and stable spectral collocation solutions to initial-boundary value problems attached to some challenging nonlinear wave equations defined on unbounded domains. We argue that spectral collocation based on Hermite and sinc functions actually provide such solutions avoiding the empirical domain truncation or any shooting techniques.

Authors

Călin-Ioan Gheorghiu
Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy

Keywords

Hermite; sinc; collocation; nonlinear; wave equation; shock like solution.

References

See the expanding block below.

Cite this paper as

C.I. Gheorghiu, Stable spectral collocation solutions to Cauchy problems for nonlinear dispersive wave equations, Proceedings of the 4th Conference of Mathematical Society of Moldova (CMSM4), 2017, pp. 277-280. ISBN 978-9975-71-915-5

PDF

https://ibn.idsi.md/sites/default/files/imag_file/277_280_Stable%20Spectral%20Collocation%20Solutions%20to%20Cauchy%20Problems%20for%20Nonlinear.pdf

About this paper

Journal

Proceedings of the 4th Conference of Mathematical Society of Moldova

Publisher Name

Academy of Sciences of Moldova

DOI
ISBN

ISBN 978-9975-71-915-5

Google Scholar Profile

?

[1] J.P. Boyd. Spectral Methods Using Rational Basis Functions on an Infinite interval. J. Comput. Phys., 69 (1987), pp. 112–142.

[2] B. Fornberg, A. Driscoll. A Fast Spectral Algorithm for Nonlinear Wave Equations with Linear Dispersion, J. Comput. Phys., 155 (1999), pp. 456–467.

[3] C.I. Gheorghiu, Spectral Methods for Non Standard Eigenvalue Problems. Fluid and Structural Mechanics and Beyond. Springer, 2014.

[4] C.I. Gheorghiu. Stable spectral collocation solutions to a class of Benjamin Bona Mahony initial value problems, Appl. Math. Comput. vol. 273 (2016), pp. 1090–1099.

[5] C.I. Gheorghiu. High Order Collocation Solutions to Problems on Unbounded Domains. Manuscript in progress.

[6] L.N. Trefethen. Spectral Methods in Matlab, SIAM Philadelphia, 2000.

277_280_Stable Spectral Collocation Solutions to Cauchy Problems for Nonlinear

Stable Spectral Collocation Solutions to Cauchy Problems for Nonlinear Dispersive Wave Equations

Călin-Ioan Gheorghiu

Abstract

In this paper we are concerned with accurate and stable spectral collocation solutions to initial-boundary value problems attached to some challenging nonlinear wave equations defined on unbounded domains. We argue that spectral collocation based on Hermite and sinc functions actually provide such solutions avoiding the empirical domain truncation or any shooting techniques.

Keywords: Hermite, sinc, collocation, nonlinear, wave equation, shock like solution.

1 Introduction

The most useful technique to solve initial-boundary value problems attached to nonlinear parabolic equations on unbounded domains (half line or the real line) involve the truncation of the domain to a finite computational one, say [ x L , x R ] x L , x R [x_(L),x_(R)]\left[x_{L}, x_{R}\right][xL,xR], with approximate boundary conditions imposed at x = x L x = x L x=x_(L)x=x_{L}x=xL and x = x R x = x R x=x_(R)x=x_{R}x=xR. One of the most difficult numerical issue for such technique is the sensitivity of a correct numerical solution to the appropriate boundary conditions, especially the one imposed at the right-hand boundary. In order to avoid this tedious discussion on the proper boundary conditions at the ends of the computational domain we will try to solve the aforementioned problems by Hermite collocation (HC) and sinc collocation (SiC).
(C)2017 by Călin-Ioan Gheorghiu
In [1] the author observes that for problems on unbounded domains boundary conditions are usually "natural" rather than "essential" in the sense that the singularities of the differential equation will force the numerical solution to have the correct behavior at infinity even if no constraints are imposed on the basis functions. In this respect our initial-boundary value problems reduce to some Cauchy problems.

2 Nonlinear wave equations with linear dispersion

We are concerned with non-periodic spectral collocation solutions for initial value problems attached to nonlinear wave equations of the form
(1) u t = N ( u ) + L ( u ) + g ( x , t ) , − ∞ ≤ x ≤ ∞ , t ≥ 0 . (1) u t = N ( u ) + L ( u ) + g ( x , t ) , − ∞ ≤ x ≤ ∞ , t ≥ 0 . {:(1)u_(t)=N(u)+L(u)+g(x","t)","-oo <= x <= oo","t >= 0.:}\begin{equation*} u_{t}=N(u)+L(u)+g(x, t),-\infty \leq x \leq \infty, t \geq 0 . \tag{1} \end{equation*}(1)ut=N(u)+L(u)+g(x,t),−∞≤x≤∞,t≥0.
The term N ( u ) N ( u ) N(u)N(u)N(u) is a genuinely nonlinear one and may also depend on u x , u x x u x , u x x u_(x),u_(xx)u_{x}, u_{x x}ux,uxx, etc. and the linear part is of the form
(2) L ( u ) := c ( t ) i m + 1 ( ∂ m u / ∂ x m ) , (2) L ( u ) := c ( t ) i m + 1 ∂ m u / ∂ x m , {:(2)L(u):=c(t)i^(m+1)(del^(m)u//delx^(m))",":}\begin{equation*} L(u):=c(t) i^{m+1}\left(\partial^{m} u / \partial x^{m}\right), \tag{2} \end{equation*}(2)L(u):=c(t)im+1(∂mu/∂xm),
but more general dispersive terms are also treatable. The forcing term g ( x , t ) g ( x , t ) g(x,t)g(x, t)g(x,t) can be embedded into N ( u ) N ( u ) N(u)N(u)N(u). The real function c ( t ) c ( t ) c(t)c(t)c(t) is often a constant.
The Benjamin Bona Mahony (BBM) type problems have been considered in our previous paper [4]. The Korteweg-de Vries (KdV), the nonlinear Schrödinger (NLS) and the Fisher's initial value problems are more challenging examples of such problems which will be partially addressed now.

3 Numerical analysis

The spectral collocation is based alternatively on the scaled Hermite and sinc functions. This spatial discretization approach avoids periodicity (see [2]) and frequently used empirical domain truncation (see
[3]). In order to march in time we use TR-BDF2 (ode23tb built in routine in MATLAB), the trapezoidal rule using a "free" interpolant (ode23t) and a modified Rosenbrock formula of order 2 (ode23s) FD schemes. We show that the method of lines ( MoL ) involved is stable using the pseudospectra of the linearized spatial discretization operators (see also [6]). The sinc collocation along with TR-BDF2 perform better than the other methods with respect to the accuracy and the computational effort. A heuristic explanation is provided.
The extent at which some invariants are conserved over time has been analyzed in our contribution [5]. It also proved to be fairly useful in optimizing the scaling parameters.

3.1 Fisher's equation with nonlocal boundary conditions

To be more specific, we define L ( u ) := u x x L ( u ) := u x x L(u):=u_(xx)L(u):=u_{x x}L(u):=uxx and N ( u ) := ρ u ( 1 − u ) N ( u ) := ρ u ( 1 − u ) N(u):=rho u(1-u)N(u):=\rho u(1-u)N(u):=ρu(1−u) in (1) where ρ ρ rho\rhoρ stands for the reaction factor, i.e. the Fisher's equation. We are mainly interested in super speed waves (SSW). With an increase in ρ ρ rho\rhoρ, the propagating front steepens and this presents a challenging numerical problem in order to resolve as well as to track the front. For the infinite spatial domain, the rapidly varying shock front is considered to be stiff with the stiffness depending on ρ ρ rho\rhoρ.
Figure 1. a) SSW time dependent profiles of Fisher's equation at t = 0 t = 0 t=0t=0t=0, t = 3.3065 e − 04 , t = 8.3189 e − 04 t = 3.3065 e − 04 , t = 8.3189 e − 04 t=3.3065 e-04,t=8.3189 e-04t=3.3065 e-04, t=8.3189 e-04t=3.3065e−04,t=8.3189e−04 and t = 0.0013 t = 0.0013 t=0.0013t=0.0013t=0.0013. b) The absolute values of the expansion coefficients of the solution at t = 0.0013 t = 0.0013 t=0.0013t=0.0013t=0.0013.

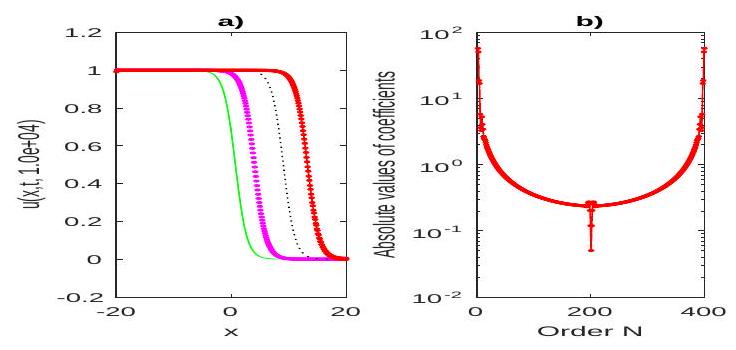
4 Conclusion

The effectiveness of our approach has been confirmed by some challenging numerical experiments. Using SiC along with TR-BDF2 we have succeeded in capturing shock like solutions to Fisher's problem (see Fig. 3.1 a)). With FFT we get the expansion coefficients of the final solution. Their decreasing behavior is reported in Fig. 3.1 b).

References

[1] J.P. Boyd. Spectral Methods Using Rational Basis Functions on an Infinite interval. J. Comput. Phys. vol. 69. (1987), pp. 112-142.
[2] B. Fornberg, A. Driscoll. A Fast Spectral Algorithm for Nonlinear Wave Equations with Linear Dispersion, J. Comput. Phys. vol. 155(1999), pp. 456-467.
[3] C.I. Gheorghiu. Spectral Methods for Non Standard Eigenvalue Problems. Fluid and Structural Mechanics and Beyoud. Springer, 2014.
[4] C.I. Gheorghiu. Stable spectral collocation solutions to a class of Benjamin Bona Mahony initial value problems, Appl. Math. Comput. vol. 273 (2016), pp. 1090-1099.
[5] C.I. Gheorghiu. High Order Collocation Solutions to Problems on Unbounded Domains. Manuscript in progress.
[6] L.N. Trefethen. Spectral Methods in Matlab, SIAM Philadelphia, 2000.
Călin-Ioan Gheorghiu
Romanian Academy, "T. Popoviciu" Institute of Numerical Analysis, Cluj-Napoca
Email: ghcalin@ictp.acad.ro
2017

Related Posts