Abstract
Numerical schemes for advection-dominated transport problems are are evaluated in a comparative study. Explicit and implicit finite difference methods are analyzed together with a global random walk algorithm in the frame of a splitting procedure. The efficiency of the methods with respect to the control of the numerical diffusion is investigated numerically on one-dimensional problems with constant coefficients and two-dimensional problems with variable coefficients consisting of realizations of space-random functions.
Authors
Nicolae Suciu
Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy, Cluj-Napoca, Romania
Imre Boros
Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy, Cluj-Napoca, Romania
Keywords
Advection-dominated transport; Numerical diffusion; Finite differences; Method of lines; Global random walk
Paper coordinates
N. Suciu, I. Boros, Controlling numerical diffusion in solving advection-dominated transport problems, J. Numer. Anal. Approx. Theory, 53 (2024) no. 1, pp, 144–157, https://doi.org/10.33993/jnaat531-1438
About this paper
Journal
Journal of Numerical Analysis and Approximation Theory
Publisher Name
Romanian Academy
Print ISSN
2457-6794
Online ISSN
ISSN-E 2501-059X
google scholar link
[1] D.L. Book, C. Li, G. Patnaik and F.F. Grinstein, Quantifying residual numerical diffusion in flux-corrected transport algorithms, J. Sci. Comp. 6(3) (1991), 323–243. https://dx.doi.org/10.1007/BF01062816 DOI: https://doi.org/10.1007/BF01062816
[2] F. Brunner, F.A. Radu, M. Bause and P. Knabner, Optimal order convergence of a modified BDM1 mixed finite element scheme for reactive transport in porous media, Adv. Water Resour. 35 (2012), 163–171. https://dx.doi.org/10.1016/j.advwatres.2011.10.001 DOI: https://doi.org/10.1016/j.advwatres.2011.10.001
[3] C.J.M. Hewett, Consistency and numerical diffusion (2021). https://www.youtube.com/watch?v=Cjb4YtgeIn0&t=263s
[4] P. Knabner and L. Angermann, Numerical methods for elliptic and parabolic partial differential equations, Springer, New York, 2003. https://doi.org/10.1007/b97419 DOI: https://doi.org/10.1007/b97419
[5] D. Kuzmin, Explicit and implicit FEM-FCT algorithms with flux linearization, J. Comput. Phys. 228(7) (2009), 2517–2534. https://dx.doi.org/10.1016/j.jcp.2008.12.011 DOI: https://doi.org/10.1016/j.jcp.2008.12.011
[6] D. Kuzmin, A. Hannukainen and S. Korotov, A new a posteriori error estimate for convection-reaction-diffusion problems, J. Comput. Appl. Math. 218(1) (2008), 70–78. https://dx.doi.org/10.1016/j.cam.2007.04.033 DOI: https://doi.org/10.1016/j.cam.2007.04.033
[7] M. Ohlberger and C. Rohde, Adaptive finite volume approximations of weakly coupled convection dominated parabolic systems, IMA J. Numer. Anal. 22(2) (2002), 253–280. https://dx.doi.org/10.1093/imanum/22.2.253 DOI: https://doi.org/10.1093/imanum/22.2.253
[8] F.A. Radu, N. Suciu, J. Hoffmann, A. Vogel, O. Kolditz, C-H. Park and S. Attinger, Accuracy of numerical simulations of contaminant transport in heterogeneous aquifers: a comparative study, Adv. Water Resour. 34 (2011), 47-61. https://dx.doi.org/10.1016/j.advwatres.2010.09.012 DOI: https://doi.org/10.1016/j.advwatres.2010.09.012
[9] W.E. Schiesser and G.W. Griffiths, A compendium of partial differential equation models: method of lines analysis with Matlab, Cambridge University Press, 2009. https://doi.org/10.1017/CBO9780511576270 DOI: https://doi.org/10.1017/CBO9780511576270
[10] J.C. Strikwerda, Finite Difference Schemes and Partial Differential Equations, SIAM, 2004. https://doi.org/10.1137/1.9780898717938 DOI: https://doi.org/10.1137/1.9780898717938
[11] N. Suciu, Diffusion in random velocity fields with applications to contaminant transport in groundwater, Adv. Water Resour. 69 (2014), 114–133. http://dx.doi.org/10.1016/j.advwatres.2014.04.002 DOI: https://doi.org/10.1016/j.advwatres.2014.04.002
[12] N. Suciu, Diffusion in Random Fields. Applications to Transport in Groundwater, Birkhäuser, Cham, 2019. https://doi.org/10.1007/978-3-030-15081-5 DOI: https://doi.org/10.1007/978-3-030-15081-5
[13] N. Suciu, L. Schüler, S. Attinger and P. Knabner, Towards a filtered density function approach for reactive transport in groundwater, Adv. Water Resour. 90 (2016), 83–98. https://dx.doi.org/10.1016/j.advwatres.2016.02.016 DOI: https://doi.org/10.1016/j.advwatres.2016.02.016
[14] C. Vamoș, N. Suciu and H. Vereecken, Generalized random walk algorithm for the numerical modeling of complex diffusion processes, J. Comput. Phys. 186 (2003), 527–544. https://doi.org/10.1016/S0021-9991(03)00073-1 DOI: https://doi.org/10.1016/S0021-9991(03)00073-1
Paper (preprint) in HTML form
.
Controlling numerical diffusion in solving advection-dominated transport problems
Abstract.
Numerical schemes for advection-dominated transport problems are evaluated in a comparative study. Explicit finite difference methods are analyzed together with a global random walk algorithm in the frame of a splitting procedure. A robust implementation of the method of lines is also proposed as an alterative approach. The efficiency of the methods with respect to the control of the numerical diffusion is investigated numerically in one-dimensional problems with constant coefficients and two-dimensional problems with variable coefficients consisting of realizations of space-random functions.
Key words and phrases:
advection-dominated transport, numerical diffusion, finite differences, method of lines, global random walk2005 Mathematics Subject Classification:
76R50, 76R99, 65M06, 65M20, 65M75,1. Introduction
The numerical diffusion in transport problems is produced when the advection velocity is nonzero, increases with the decrease of the diffusion coefficient, and is often associated with spurious oscillations of the solution [5]. Remedies to these issues are provided by flux corrected transport and other diffusion-antidiffusion methods [2, 6], upwind schemes [7, 3], or adaptive finite volume approximations [8].
Numerical diffusion in advection-diffusion problems may be produced by the finite order of the approximations and/or by numerically induced smoothing. In such circumstances, a small amount of numerical diffusion may occur even when the velocity vanishes [2, 9]. But above all, the numerical diffusion cannot be avoided when stabilizing upwind schemes are used to prevent oscillations of the numerical solution [9]. To illustrate this situation let us consider the advection equation,
and the finite difference (FD) scheme with upwind space discretization,
which provides solutions at
where
Performing Taylor expansions of
The above relation shows that the FD scheme is unstable for Courant number
Although, in general, discrete error norms used to measure differences from reference solutions do not discriminate between different sources of errors (e.g., discretization, truncation, numerical diffusion) a quantification of the numerical diffusion is sometimes obtained, for nonsteady transport problems, by using the spatial moments of the solution [6, 9]. For constant velocity and diffusion coefficients, it was found that the diffusion coefficient estimated from the second central spatial moment of the concentration computed with different numerical schemes (linear and quadratic finite element methods with and without upwind, different mixed-finite element implementations, and finite volume methods) is affected by errors of the order of the nominal diffusion coefficient, which can hardly be reduced by refining the discretization for mesh Péclet numbers
2. One-dimensional advection-diffusion process with constant coefficients
The advection-diffusion process used in the following to test one-dimensional (1D) numerical schemes is governed by the parabolic equation with constant coefficients
| (1) |
with analytical solution given by the normalized Gaussian function
| (2) |
The constant coefficients in Eq. (1) are chosen as
Accuracy estimates are done by comparisons of the numerical solution
| (3) |
2.1. Global random walk and equivalent finite difference schemes
The 1D GRW algorithm approximates the solution of (1) by
| (4) | |||
| (5) |
where the amplitude of the diffusion jumps
| (6) |
Giving up particles indivisibility one obtains a deterministic FD scheme.
Summing up the contributions (5) to
| (7) |
Fig. 2 shows that the velocity
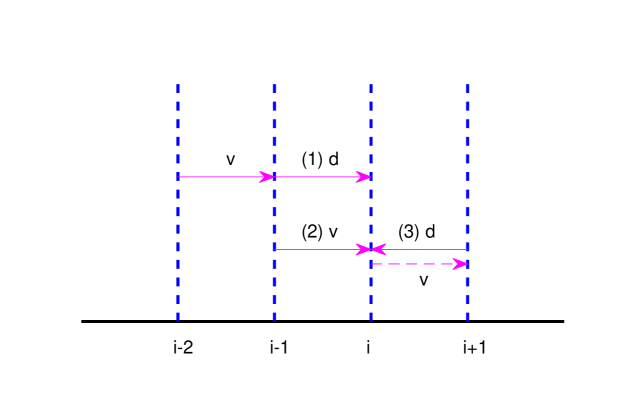
The FD scheme (7) is equivalent to a splitting FD scheme with the following advection (a) and diffusion (d) steps:
| (8) | |||||
| (9) |
The advection scheme (8) is the discrete version of the exact
solution of the advection equation,
Since the dimensionless velocity has to be an integer greater than unity, the GRW splitting-scheme (8)-(9) is defined for integer Courant numbers
One remarks that the GRW-advection scheme (8) is a particular case, for Courant number
| (10) |
and of the BOX scheme
| (11) |
While the UPW scheme is stable only if
2.2. Method of Lines
The Method of Lines (MOL) is an effective numerical technique for solving partial differential equations (PDEs), particularly useful in advection-dominated transport problems. This method discretizes the spatial domain while preserving the time domain as continuous, thereby transforming the PDE into a system of ordinary differential equations (ODEs). These ODEs are subsequently solved using established ODE solvers, providing a robust framework for addressing the challenges inherent in advection-dominated scenarios. For more details on the MOL, consult [10].
If we consider a discretization with
For improved accuracy, higher-order FD approximations can be derived using Taylor series expansions. The derivation is achieved by combining multiple Taylor series expansions at different points such that the lower-order terms cancel out, leaving higher-order terms as the dominant source of error.
In the following, we use the central-space FD approximation
| (12) |
where
| (13) |
| (14) |
Since Eq. (14) constitutes
In the system of ODE (14) we have
which reduces to
In this study, we employed the explicit fourth-order Runge-Kutta method to solve the resulting system of ODEs. We experimented with various Courant numbers to determine the threshold for significant numerical errors. With a spatial step size of
2.3. Accuracy estimates
The accuracy of the numerical solutions presented in Fig. 3 is evaluated by the quadratic norm,
| (15) |
Similarly to (15), the accuracy of the estimated coefficients
| (16) |
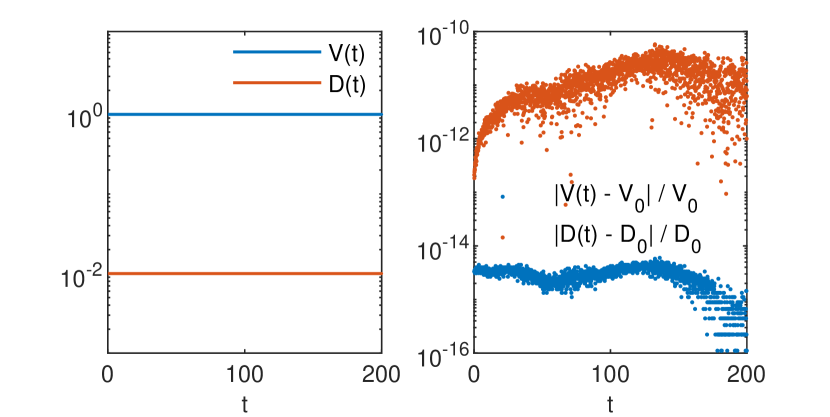
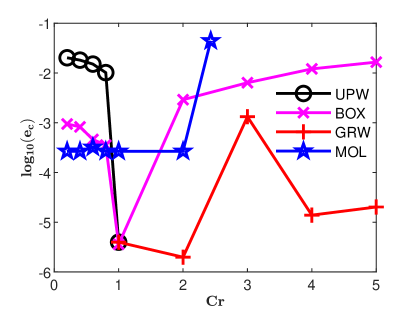
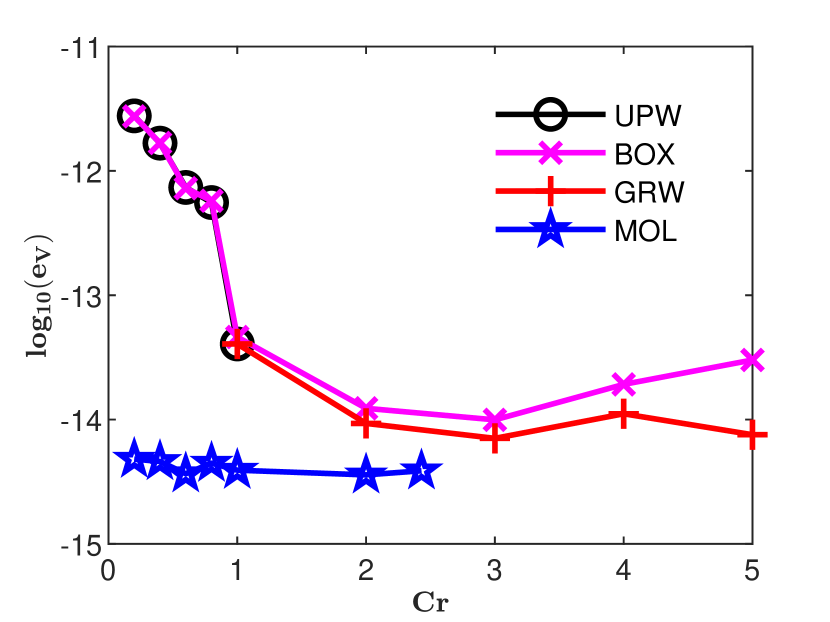
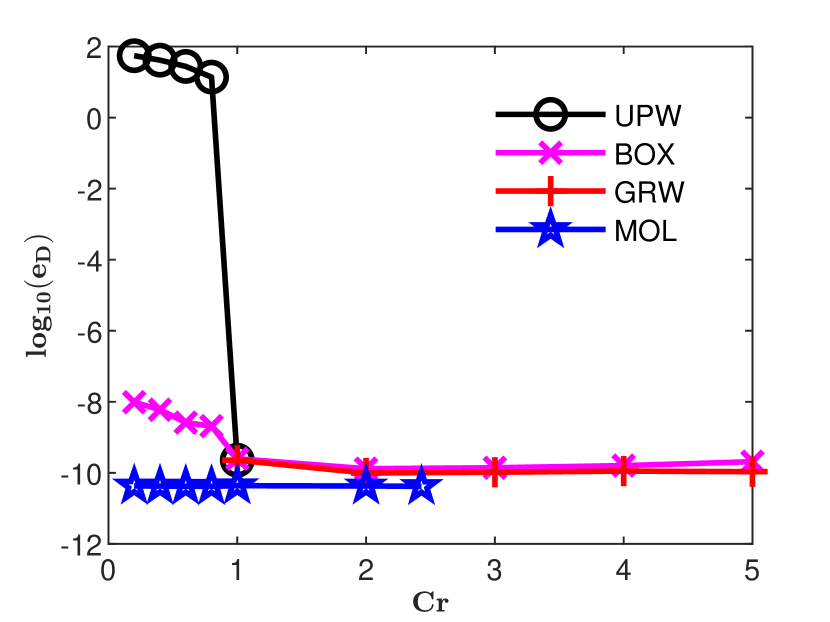
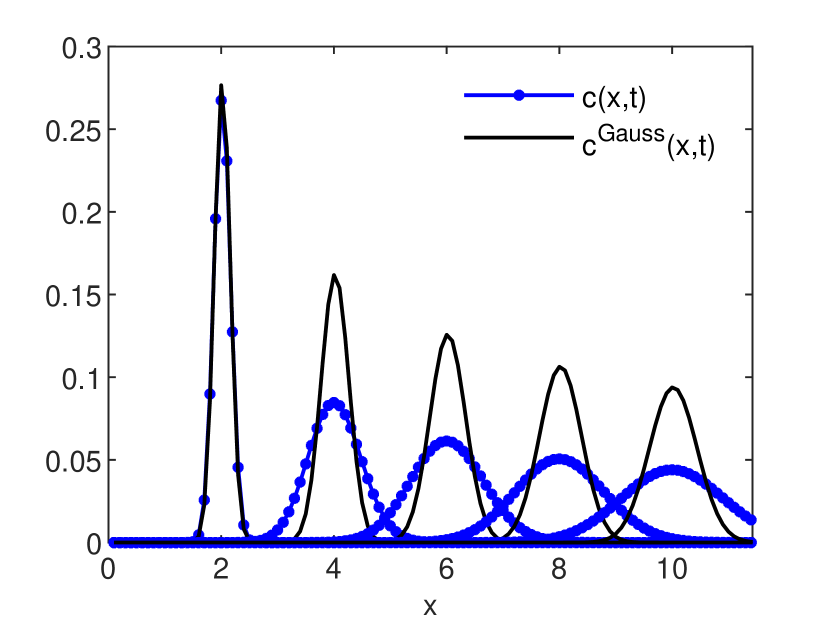
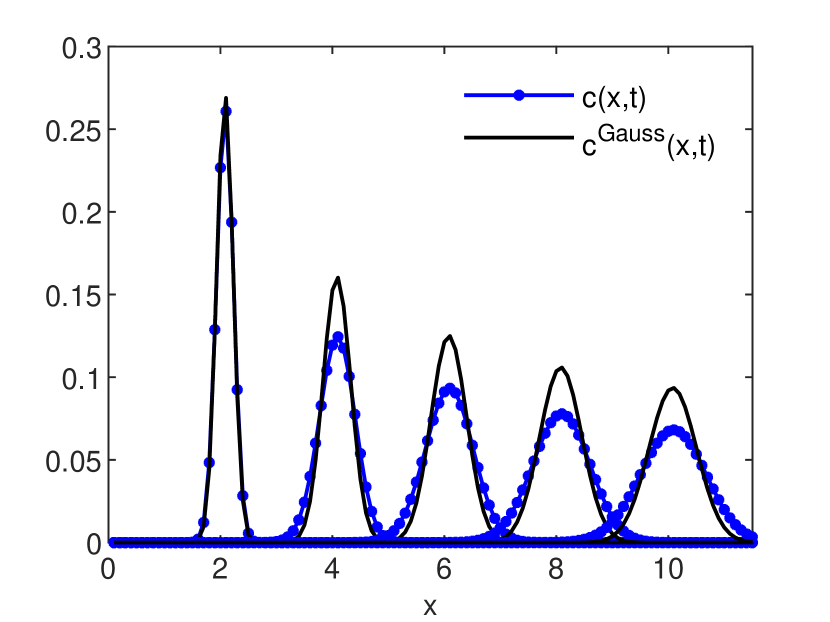
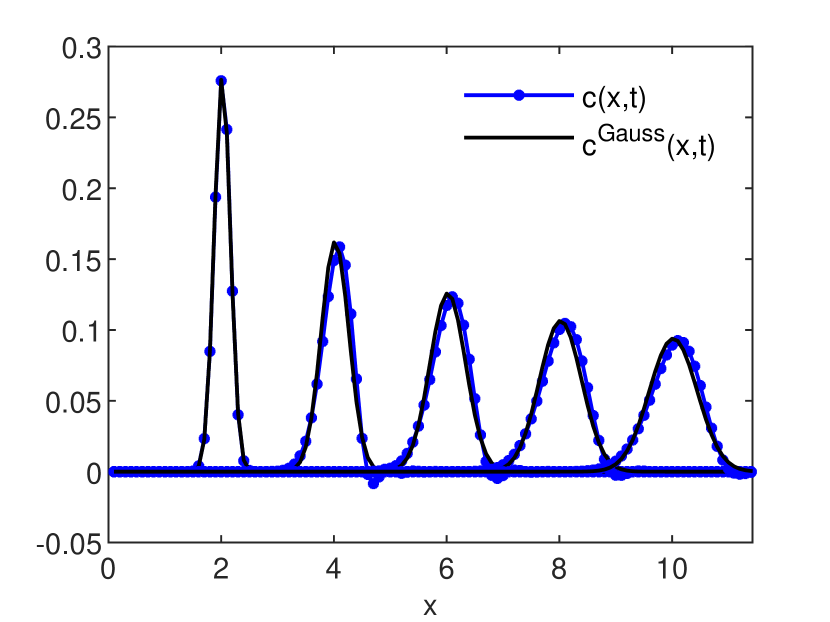
is an estimation, global in time, of the numerical diffusion (see also [6, 9]). The accuracy estimates for the GRW-FD, UPW, BOX, and MOL schemes are presented in Figs. 3 and 4. In Figs. 5, 6 and 7 the numerical solutions of the four schemes are compared to the exact Gaussian solution (2) at successive times
Estimations (16) of numerical diffusion corresponding to the splitting GRW-FD scheme (8)-(9), UPW scheme (10), and BOX scheme (11) are presented in Fig. 4, right panel. The computations were carried out for a fixed space step
One remarks that in case
As seen in Fig. 4, the GRW-FD scheme is practically free of numerical diffusion. Moreover, since the advection step (8) in the splitting procedure is the FD approximation of exact solution of the advection equation, the GRW-FD scheme reproduces almost perfectly the shape of the analytical solution, within the range of the errors shown in Fig. 3.
A special attention deserves the performance of the MOL scheme. The errors of the solution shown in Fig. 3 are of the order
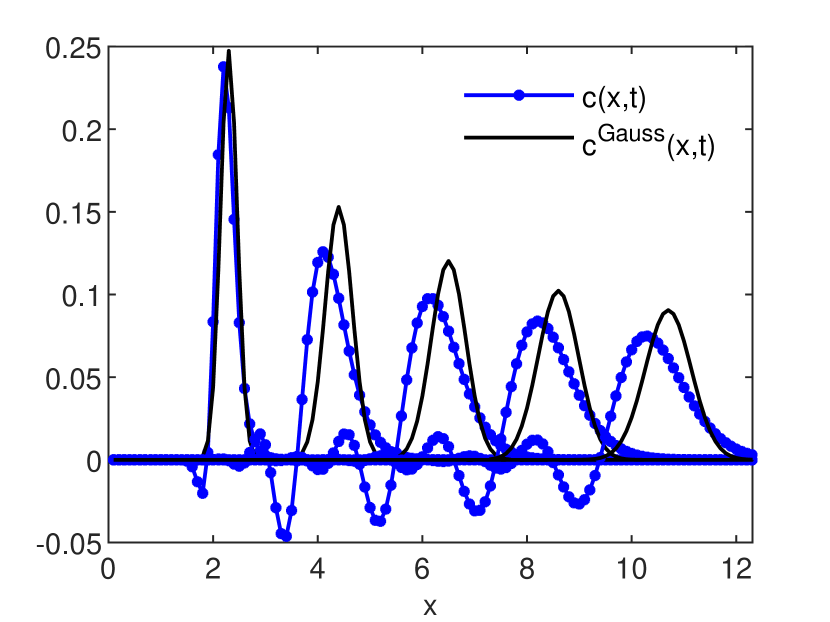
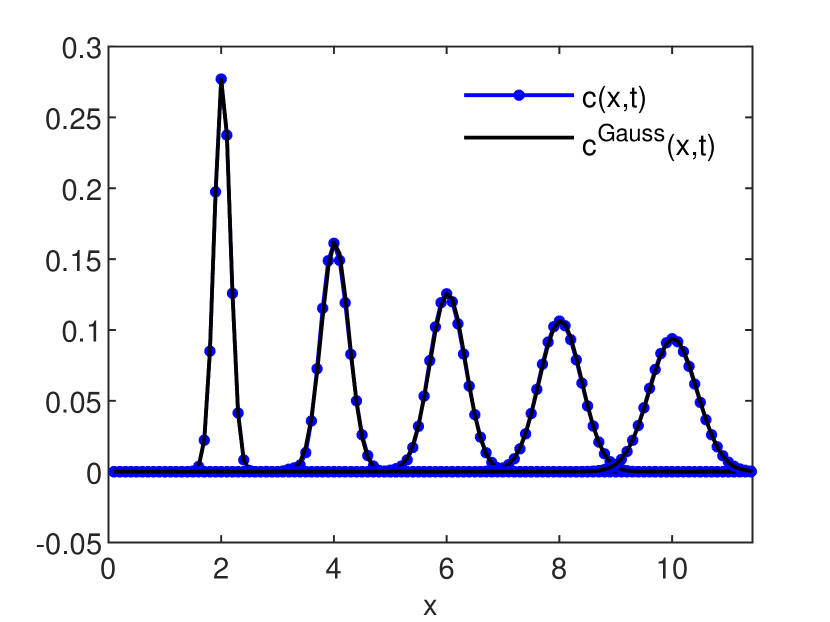
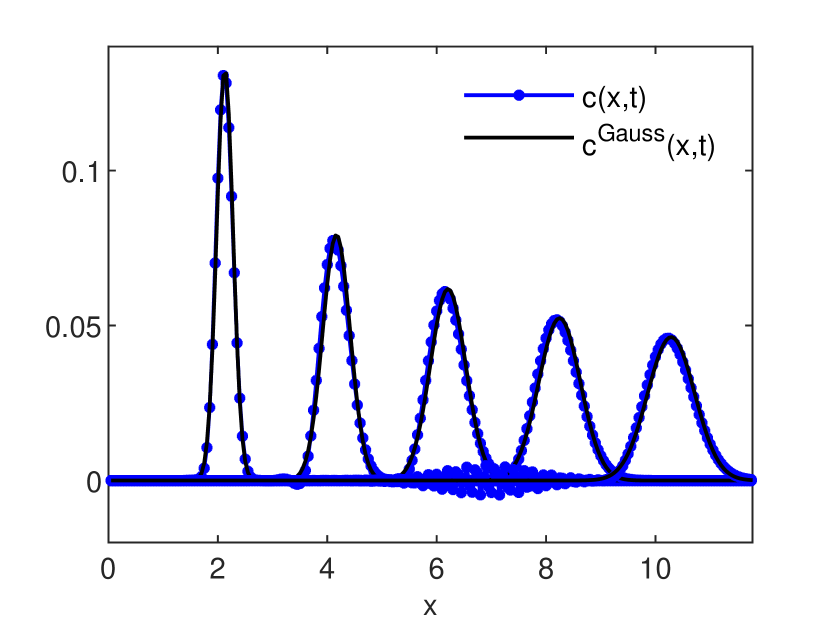
3. Two-dimensional diffusion with variable drift coefficients
In the following, we consider a 2D transport problem consisting of a diffusion process in a spatially variable velocity field, governed by the equation
| (17) |
where the solution
We choose
| (18) |
and similarly for
Fig. 9 shows a numerical solution of Eq. (17) with the above parameters, obtained by repeating the 1D GRW procedure (4)-(6) in both spatial directions. Estimations of the effective coefficients (18) for the same problem are presented in Fig. 9.
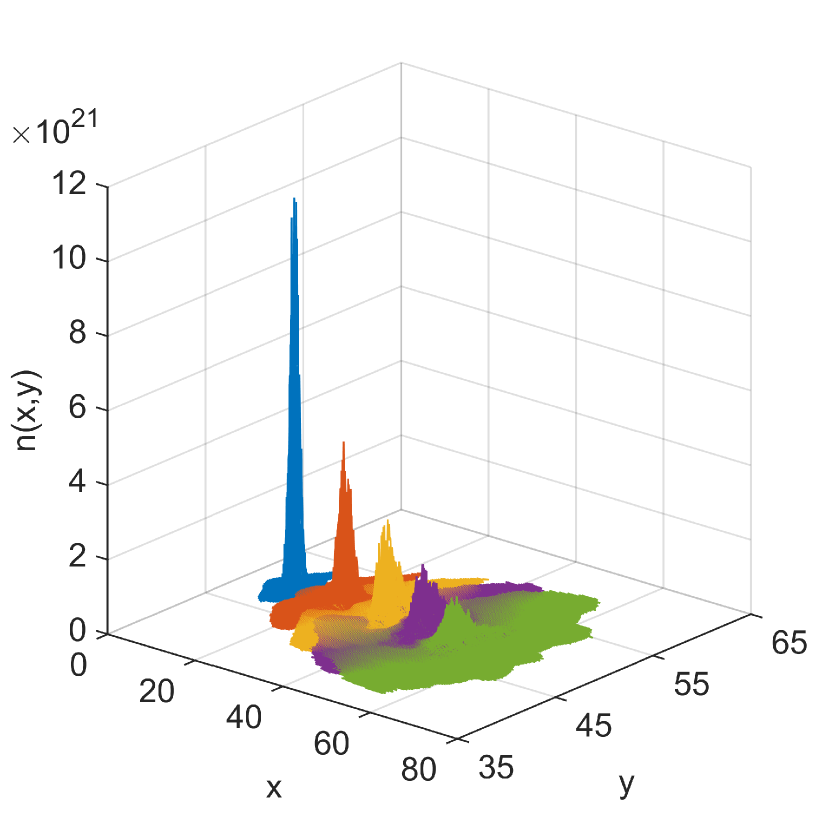
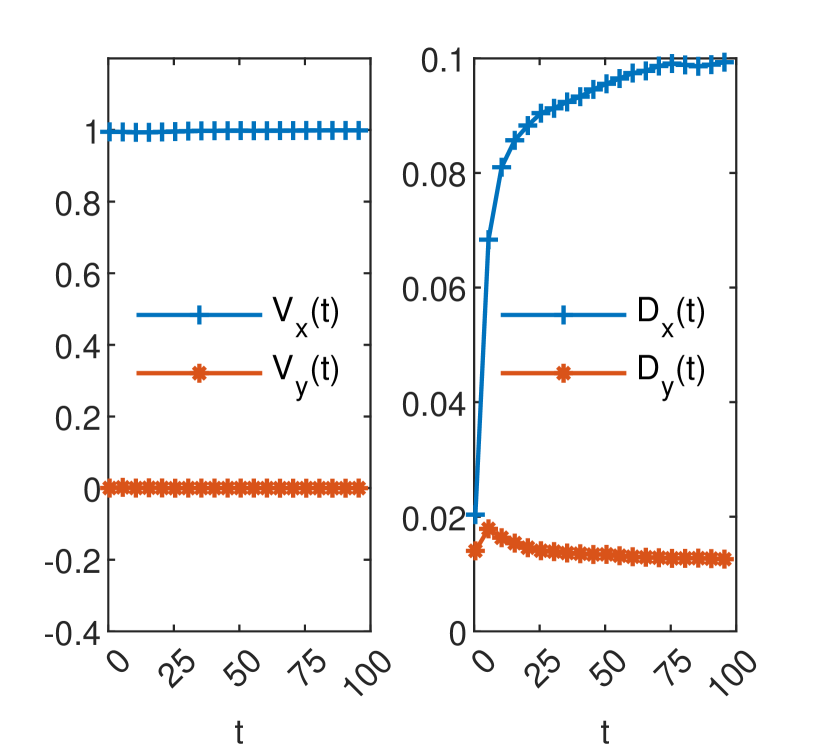
The numerical schemes evaluated in the following solve Eq. (17) in a spatial domain
3.1. Biased GRW algorithm
The biased-GRW algorithm (BGRW) accounts for the advective terms in Eq. (17) by increasing the probability that a random walker takes a jump in the flow direction and decreasing the jump probability in the opposite direction.
The two-dimensional BGRW is defined by the relation
| (19) | |||||
where
| (20) |
Instead of the unbiased GRW rule (6), the average numbers of jumps in the BGRW algorithm (19) are now given by
| (21) |
As follows from (21), the BGRW algorithm is subject to the following restrictions
| (22) |
By the last two inequalities in (22), the Courant numbers
3.2. Unbiased GRW scheme
Since the diffusion coefficient is constant, the unbiased GRW solutions to the transport problem formulated in the beginning of this section are obtained in two steps, first by performing the 1D GRW procedure (4)-(6) in the
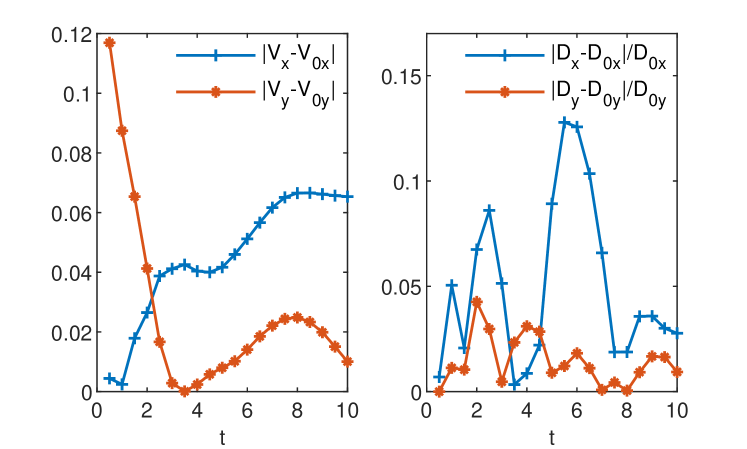
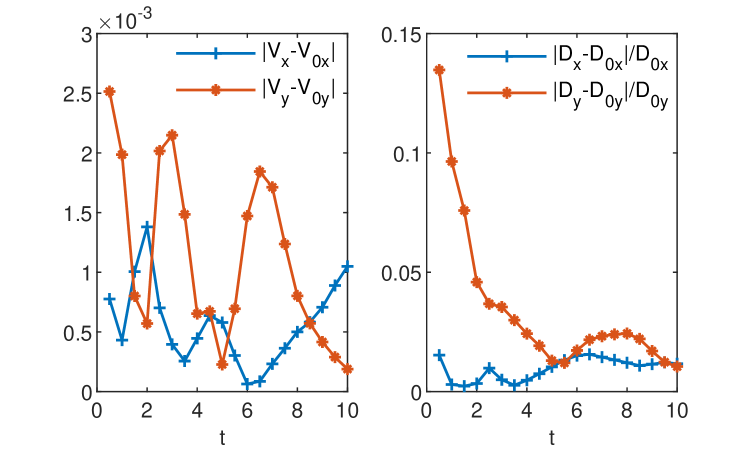
Errors of GRW estimates of the effective coefficients for a single realization of the random velocity field are presented in Fig. 10 and errors of the ensemble averaged coefficients (18) are presented in Fig. 11. For a fixed realization of the velocity field (Fig. 10) the relative errors of the unbiased GRW scheme range from a few percents to more than
4. Conclusions
The numerical diffusion in advection-dominated problems can be directly estimated by comparing the diffusion coefficient derived from the spatial moments of the numerical solution to the nominal coefficient. However, since this is a global estimate, it does not guarantee that the numerical scheme accurately reproduces the shape of the exact solution of the transport problem.
In this study, we compared the performance in solving the one-dimensional advection-diffusion equation with constant coefficients of two classical FD schemes, UPW and BOX, an unbiased GRW scheme, and a MOL scheme. For Courant number
The GRW scheme is by construction free of numerical diffusion. Additionally, since it performs advective displacements according to the exact solution of the advection equation, the unbiased GRW scheme preserves the shape of the exact solution for any integer
For the purpose of practical applications for two-dimensional simulations of transport in groundwater, the unbiased GRW has been evaluated through comparisons with the BGRW scheme, which simulates advection by using biased jump probabilities. The BGRW scheme is highly accurate but much slower than the unbiased scheme. The unbiased GRW is faster because it is not not constraint by small Courant numbers, but, for the same reason, it is less accurate due to the overshooting errors. However, the average over an ensemble of realizations of the random velocity field, which model the heterogeneity of the aquifer system, reduces the effect of the overshooting and the unbiased GRW scheme is an efficient tool for assessing statistical inferences on the transport process.
References
- [1]
- [2] D.L. Book, C. Li, G. Patnaik and F.F. Grinstein, Quantifying residual numerical diffusion in flux-corrected transport algorithms, J. Sci. Comp. 6(3) (1991), 323–243. https://dx.doi.org/10.1007/BF01062816
- [3] F. Brunner, F.A. Radu, M. Bause M and P. Knabner, Optimal order convergence of a modified BDM1 mixed finite element scheme for reactive transport in porous media, Adv. Water Resour. 35 (2012), 163–171. https://dx.doi.org/10.1016/j.advwatres.2011.10.001
- [4] C.J.M. Hewett, Consistency and numerical diffusion (2021). https://www.youtube.com/watch?v=Cjb4YtgeIn0&t=263s
- [5] P. Knabner and L. Angermann, Numerical methods for elliptic and parabolic partial differential equations, Springer, New York, 2003. https://doi.org/10.1007/b97419
- [6] Kuzmin, Explicit and implicit FEM-FCT algorithms with flux linearization, J. Comput. Phys. 228(7) (2009), 2517–2534. https://dx.doi.org/doi:10.1016/j.jcp.2008.12.011
- [7] D. Kuzmin, A. Hannukainen and S. Korotov, A new a posteriori error estimate for convection-reaction-diffusion problems, J. Comput. Appl. Math. 218(1) (2008), 70–78. https://dx.doi.org/10.1016/j.cam.2007.04.033
- [8] M. Ohlberger and C. Rohde, Adaptive finite volume approximations of weakly coupled convection dominated parabolic systems, IMA J. Numer. Anal. 22(2) (2002), 253–280. https://dx.doi.org/10.1093/imanum/22.2.253
- [9] F.A. Radu, N. Suciu, J. Hoffmann, A. Vogel, O. Kolditz, C-H. Park and S. Attinger, Accuracy of numerical simulations of contaminant transport in heterogeneous aquifers: a comparative study, Adv. Water Resour. 34 (2011), 47–61. https://dx.doi.org/10.1016/j.advwatres.2010.09.012
- [10] W.E. Schiesser and G.W. Griffiths, A compendium of partial differential equation models: method of lines analysis with Matlab, Cambridge University Press, 2009. https://doi.org/10.1017/CBO9780511576270
- [11] J.C. Strikwerda, Finite Difference Schemes and Partial Differential Equations, SIAM, 2004. https://doi.org/10.1137/1.9780898717938
- [12] N. Suciu, Diffusion in random velocity fields with applications to contaminant transport in groundwater, Adv. Water Resour. 69 (2014) 114-133. http://dx.doi.org/10.1016/j.advwatres.2014.04.002
- [13] N. Suciu, Diffusion in Random Fields. Applications to Transport in Groundwater, Birkhäuser, Cham, 2019. https://doi.org/10.1007/978-3-030-15081-5
- [14] N. Suciu, L. Schüler, S. Attinger and P. Knabner, Towards a filtered density function approach for reactive transport in groundwater, Adv. Water Resour. 90 (2016), 83–98. https://dx.doi.org/10.1016/j.advwatres.2016.02.016
- [15] C. Vamoş, N. Suciu and H. Vereecken, Generalized random walk algorithm for the numerical modeling of complex diffusion processes, J. Comput. Phys., 186 (2003), 527–544. https://doi.org/10.1016/S0021-9991(03)00073-1
Copyright (c) 2024 Nicolae Suciu, Imre Boros

This work is licensed under a Creative Commons Attribution 4.0 International License.
