Abstract
The aim of the present paper is to analyze the non-normality of the matrices (finite dimensional operators) which result when some Chebyshev-type methods are used in order to solve second order differential two-point boundary value problem.
We consider in turn the classical Chebyshev-tau method as well as two variants of the Chebyshev-Galerkin method. As measure of non-normality we use the non-normality ratio introduced in a previous paper. The competition between the dimension of matrices (the order of approximation) and their structure (the numerical method itself) with respect to normality is the core of our study.
It is observed that for quasi normal matrices, i.e., non-normality ratio close to 0, exhibiting pure real spectrum, this measure remains the unique indicator of non-normality. In such cases the pseudospectrum tells nothing about non-normality.
Authors
Tiberiu Popoviciu Institute of Numerical Analysis
Keywords
Non-normal matrices; scalar measure; Chebyshev spectral approximation; two point boundary value problem.
References
See the expanding block below.
Cite this paper as
C.I. Gheorghiu, On spectral properties of Chebyshev-type methods. Dimensions vs. structure, Studia Univ. Babeş-Bolyai Math., L (2005) 61-66.
About this paper
Publisher Name
Babes-Bolyai University
Paper on journal website
Print ISSN
0252-1938
Online ISSN
2065-961x
MR
?
ZBL
?
Google Scholar
?
[1] Gheorghiu, C.I., A new Scalar Measure on Non-normality. Application to the Characterization of some Spectral Methods, under evaluation at SIAM J. Sci. Comput,
[2] Gheorghiu, C.I., Pop, I.S., On the Chebyshev-tau approximation for some Singularly Perturbed Two-Point Boundary Value Problems, Rev. d’Analyse Numerique et de Theorie de l’Approximation, 24(1995), 125-129.
[3] Gottlieb, D., Orszag, S.A., Numerical Analysis of Spectral Methods: Theory and Applications, SIAM Philadelphia, 1977.
[4] Pop, I. S., Numerical approximation of differential equations with spectral methods (in Romanian), Technical report “Babes-Bolyai” University Cluj-Napoca, Faculty of Mathematics and Informatics, Cluj-Napoca, 1995.
[5] Pop, I.S., A stabilized approach for the Chebyshev-tau method, Studia Univ. “Babes-Bolyai”, Mathematica, 42(1997), 67-79.
[6] Pop, I.S., Gheorghiu, C.I., Chebyshev-Galerkin Methode for Eigenvalue Problems,Proceedings of ICAOR, Cluj-Napoca, 1996, vol. II, 217-220.
[7] Shen, J., Efficient spectral-Galerkin method II, Direct solvers of second and fourth equations using Chebyshev polynomials, SIAM J. Sci. Stat. Comput., 16(1995), 74-87.
[8] Trefethen, L.N., Computation of Pseudospectra, Acta Numerica, 1999, 247-295.
Paper (preprint) in HTML form
ON SPECTRAL PROPERTIES OF SOME CHEBYSHEV-TYPE METHODS DIMENSION VS. STRUCTURE
Abstract
The aim of the present paper is to analyze the non-normality of the matrices (finite dimensional operators) which result when some Chebyshev-type methods are used in order to solve second order differential two-point boundary value problems. We consider in turn the classical Chebyshev-tau method as well as two variants of the Chebyshev-Galerkin method. As measure of non-normality we use the non-normality ratio introduced in a previous paper. The competition between the dimension of matrices (the order of approximation) and their structure (the numerical method itself) with respect to normality is the core of our study. It is observed that for quasi normal matrices, i.e., non-normality ratio close to 0 , exhibiting pure real spectrum, this measure remains the unique indicator of non-normality. In such cases the pseudospectrum tells nothing about non-normality.
1. Introduction
2. The non-normality of CT, CGS and CG methods
Eventually, all the technicalities implied by CG method are available in the report of I. S. Pop [4]. For various values of parameters
| The variation | |||||
| CT | 1.0254 | 0.9852 | 0.9847 | 0.9845 | |
| CG | 0.3958 | 0.2220 | 0.1616 | 0.0825 | |
| CGS | 0.2926 | 0.1238 | 0.0891 | 0.0452 |
| The variation | |||||
| CT | 0.0510 | 0.9713 | 0.9845 | 0.9845 | |
| CG | 0.3584 | 0.1359 | 0.0986 | 0.0728 | |
| CGS | 0.0076 | 0.0121 | 0.0200 | 0.0538 |
| The variation | |||||
| CG | 0.4759 | 0.1972 | 0.1435 | 0.0796 | |
| CGS | 0.1979 | 0.0628 | 0.0538 | 0.0414 |
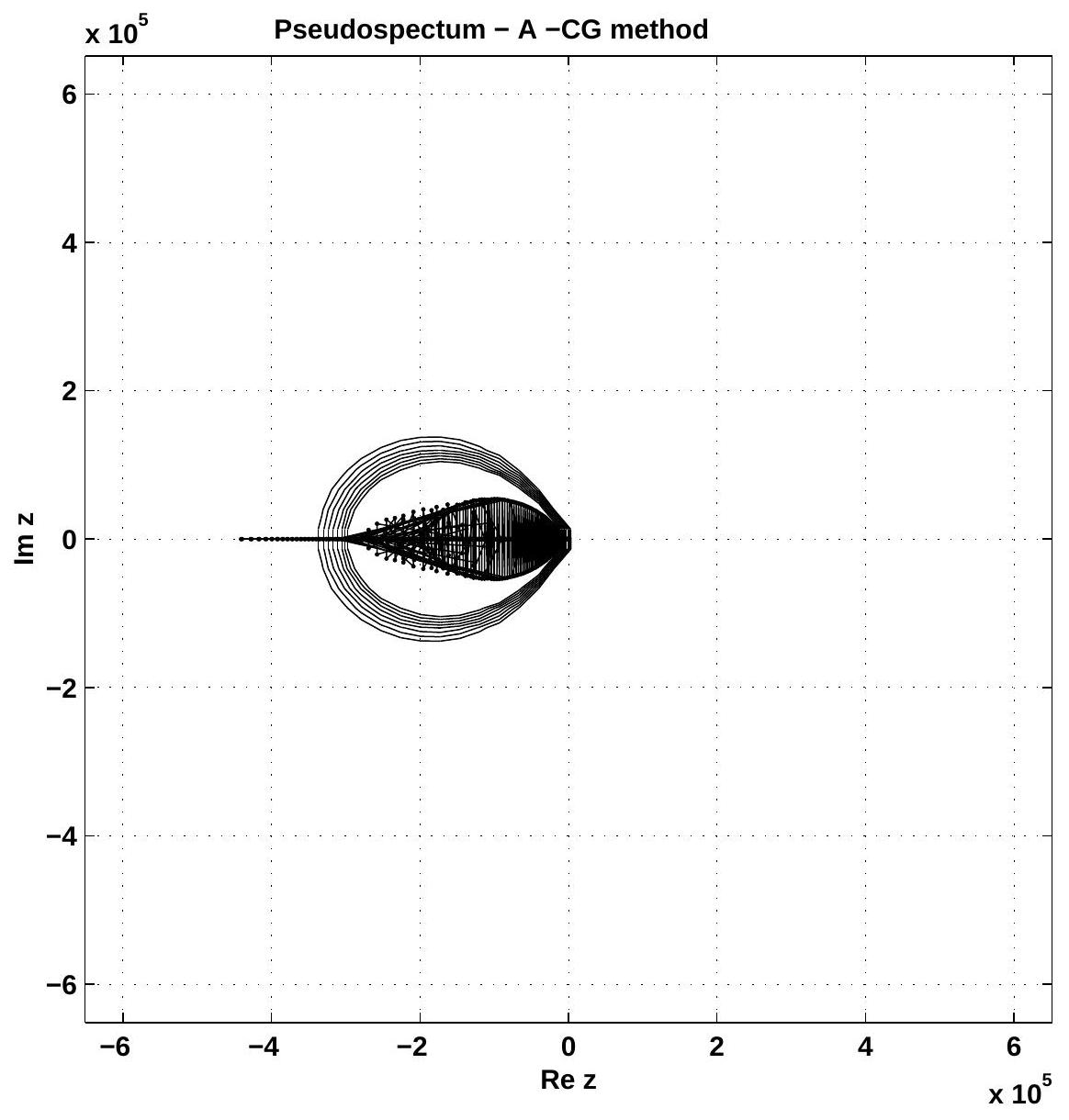
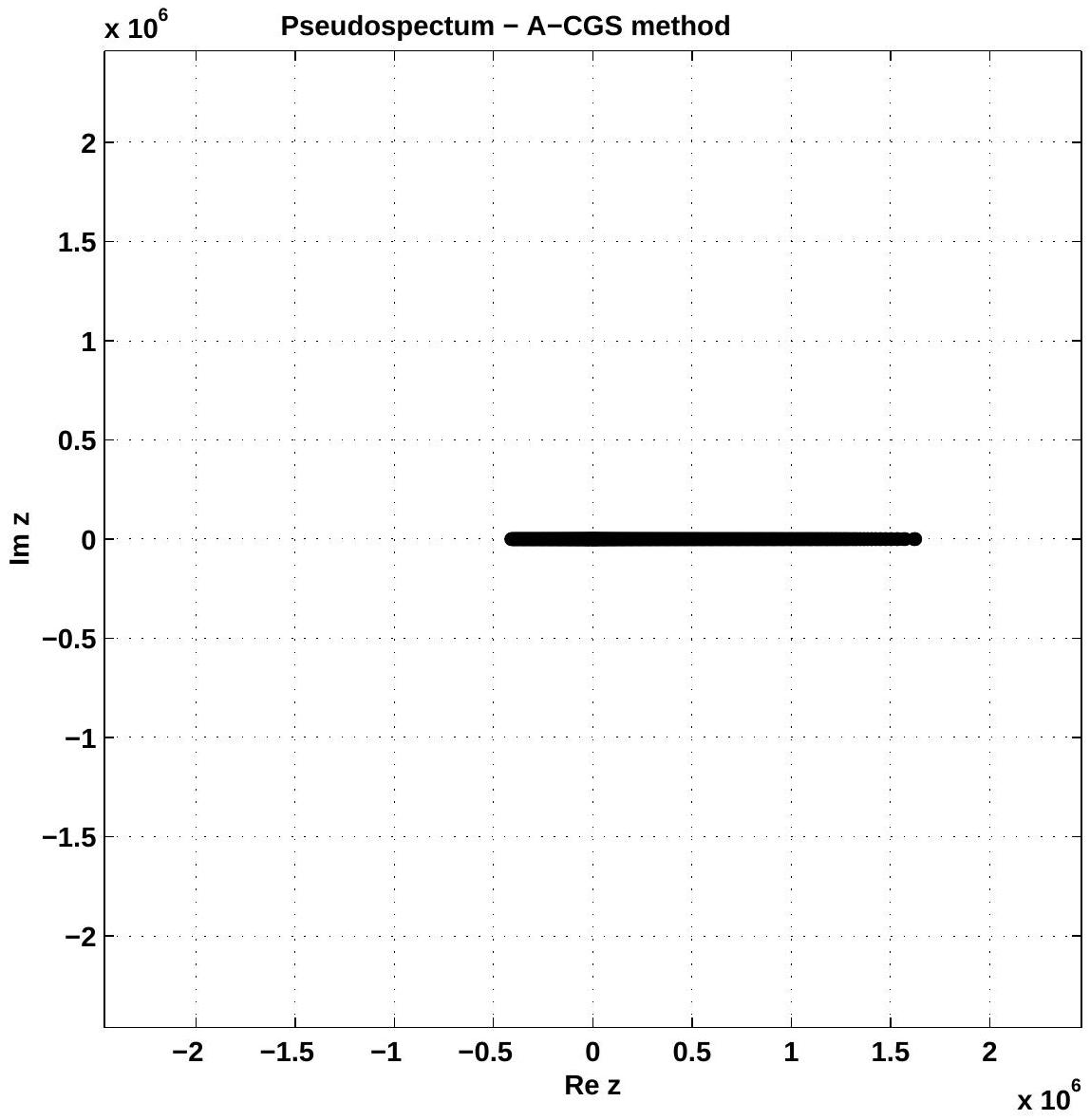
3. Concluding remarks
the same value of non-normality, CG decreasing and CGS increasing for large values of cutoff parameter
References
[2] Gheorghiu, C. I., Pop, I. S., On the Chebyshev-tau Approximation for some Singularly Perturbed Two-Point Boundary Value Problems, Rev. d'Analyse Numerique et de Theorie de l'Approximation, 24(1995), 125-129.
[3] Gottlieb, D., Orszag, S. A., Numerical Analysis of Spectral Methods: Theory and Applications, SIAM Philadelphia, 1977.
[4] Pop, I. S., Numerical approximation of differential equations with spectral methods (in Romanian), Technical report, "Babes-Bolyai" University Cluj-Napoca, Faculty of Mathematics and Informatics, Cluj-Napoca, 1995.
[5] Pop, I. S., A stabilized approach for the Chebyshev-tau method, Studia Univ. "BabesBolyai", Mathematica, 42(1997), 67-79.
[6] Pop, I. S., Gheorghiu, C. I., Chebyshev-Galerkin Methods for Eigenvalue Problems, Proceedings of ICAOR, Cluj-Napoca, 1996, vol. II, 217-220.
[7] Shen, J., Efficient spectral-Galerkin method II, Direct solvers of second and fourth equations using Chebyshev polynomials, SIAM J. Sci. Stat. Comput., 16(1995), 74-87.
[8] Trefethen, L. N., Computation of Pseudospectra, Acta Numerica, 1999, 247-295.
"T. Popoviciu" Institute of Numerical Analysis, P.O. Box 68, Cluj-Napoca 1, Romania
E-mail address: ghcalin2003@yahoo.com
- Received by the editors: 29.10.2004.
2000 Mathematics Subject Classification. 65F15, 65F35, 65L10, 65L60.
Key words and phrases. Non-normal matrices, scalar measure, Chebyshev-spectral approximation, two-point boundary value problems.
This paper was presented at International Conference on Nonlinear Operators, Differential Equations and Applications held in Cluj-Napoca (Romania) from August 24 to August 27, 2004.
