Abstract
If dark matter did exist in the form of a self-interacting boson gas, when its temperature became lower than the critical, density dependent temperature, a phase transition to a Bose-Einstein Condensate did occur in the early Universe. The presence of the condensate dark matter leads to specific signatures in the galaxy rotation, and in the dark matter density distribution. In particular Bose-Einstein Condensate (BEC) dark matter models predict a finite and well defined radius of the dark matter halo, whose numerical value depends on the mass of the dark matter particle, and of the scattering length.
We compare the theoretical predictions of the functional form of the rotation curves in the slowly rotating BEC models with the SPARC sample of measured rotation curves, by using genetic algorithms, to fit the observational data, and to obtain estimates of the relevant physical parameters of the BEC dark matter halos (central density, angular velocity and static radius).
The density profiles of the dark matter distribution are also considered, and it follows that the presence of the condensate dark matter could also provide an alternative solution for the core/cusp problem.
Authors
M. Crăciun
(Tiberiu Popoviciu Institute of Numerical Analysis)
T. Harko
(Department of Physics, Babes-Bolyai University, Cluj-Napoca, Romania and
School of Physics, Sun Yat-Sen University Guangzhou, People’s Republic of China)
Keywords
Cosmology; galactic astronomy; dark matter; Bose-Einstein condensation
References
See the expanding block below.
Paper coordinates
M. Crăciun, T. Harko, Constraining Bose-Einstein condensate dark matter models with the galaxy rotation curves of the SPARC sample, Romanian Astronomical Journal, 29 (2019) no.2, 101-118.
About this paper
Journal
Romanian Astronomical Journal
Publisher Name
Romanian Academy Publishing House (Editura Academiei Romane)
DOI
not available yet.
Print ISSN
1220-5168
Online ISSN
2285-3758
Google Scholar Profile
Constraining Bose-Einstein Condensate Dark Matter Models with the Galaxy Rotation Curves of the SPARC Sample
Abstract
If dark matter did exist in the form of a self-interacting boson gas, when its temperature became lower than the critical, density dependent temperature, a phase transition to a Bose-Einstein Condensate did occur in the early Universe. The presence of the condensate dark matter leads to specific signatures in the galaxy rotation, and in the dark matter density distribution. In particular Bose-Einstein Condensate (BEC) dark matter models predict a finite and well defined radius of the dark matter halo, whose numerical value depends on the mass of the dark matter particle, and of the scattering length. We compare the theoretical predictions of the functional form of the rotation curves in the slowly rotating BEC models with the SPARC sample of measured rotation curves, by using genetic algorithms, to fit the observational data, and to obtain estimates of the relevant physical parameters of the BEC dark matter halos (central density, angular velocity and static radius). The density profiles of the dark matter distribution are also considered, and it follows that the presence of the condensate dark matter could also provide an alternative solution for the core/cusp problem.
keywords:
Cosmology – Galactic astronomy – Dark matter – Bose-Einstein Condensation1 Introduction
The standard CDM cosmological paradigm has proven to be exceptionally successful in describing the major properties of the Universe, as well as its large scale structure (Ade et al., 2016). However, despite its success, two fundamental open questions remain unanswered by the CDM model, namely, the precise nature of the dark matter, and of the dark energy, respectively. Moreover, there is a large discrepancy between the theoretically expected and the observed values of the cosmological constant (Bull et al., 2016).
The comparison of the theoretical models with observations have also generated a number of still unresolved tensions on the galactic scales (Bullock and Boylan-Kolchin, 2017). There are (at least) three problems that have been intensively investigated. The first one is the missing satellite problem (Moore et al., 1999; Klypin et al., 1999), which follows from the significant difference between the observed number of satellite galaxies of the Milky Way and the number of substructures that appear in CDM cosmological simulations. The second problem is the too big to fail problem, which is a consequence of the observations of the low central densities of the Milky Way satellites (Boylan-Kolchin, Bullock and Kaplinghat, 2011).
A third problem that confronts present day galactic astrophysics is the so-called ‘core/cusp’ problem. The dark matter-only simulations in the CDM model predict cuspy density profiles for dark matter haloes, that is, profiles with steep central slopes, given by (Navarro, Frenk and White, 1997),
| (1) |
which behave near the origin as . On the other hand, the observations of the galaxy rotation curves indicate the existence of flat or cored profiles in the inner regions of the halos (Oh et al., 2015). There are several solutions proposed to this problem, like, for example, taking into account in the numerical simulations the effects of the baryonic feedback (Di Cintio et al., 2014). Supernovae explosions may blow large amounts of gas in the central galactic region of a galaxy, leading to a fluctuation in the gravitational potential of the gas that may also influence the dark matter distribution.
However, from a physical point of view the core-cusp problem can be easily solved (Harko, 2011) by assuming that the dark matter is in the form of a BEC (Boehmer and Harko, 2007), that is, it consists of massive bosons that gain a repulsive interaction by occupying the same ground energy state. The Bose-Einstein Condensation process takes place when the temperature of the boson gas becomes smaller than the critical temperature , given by (Pethick and Smith, 2008)
| (2) |
where is the mass of the particle in the condensate, is the critical transition density, is Boltzmann’s constant, and is the Riemmann zeta function, respectively. The Bose-Einstein condensation process was observed experimentally in 1995 in dilute alkali gases, cooled to extremely low temperatures, and confined in a magnetic trap (Anderson et al., 1995; Bradley et al., 1995; Davis et al., 1995).
The Bose-Einstein condensate dark matter is described by the nonlinear Gross-Pitaevskii equation, with the gravitational potential playing the role of the confining potential. In the Thomas-Fermi approximation, condensate dark matter can be described by a polytropic equation of state with polytropic index (Boehmer and Harko, 2007). The properties of the galactic clusters in the BEC dark matter model were considered in (Harko et al., 2015). The study of the rotating BEC halos was performed in (Zhang et al., 2018) by assuming a rigid body rotation for the halo. By using the hydrodynamic representation of the Gross-Pitaevskii equation one can obtain the basic equation describing the density distribution of the rotating condensate. The general solutions for the condensed dark matter density can then be found, as well as the general representations for the mass distribution, boundary (radius), and tangential velocity, respectively. In the first order of approximation, and under the assumption of slow rotation, explicit representations for the radius, mass, and tangential velocity can be obtained, which generalizes to the rotating case the static dark matter distribution expressions.
From the BEC dark matter model one can obtain a systematic description of the rotation velocity of massive particles in condensate galactic halos, as well of the density distribution of the halo. It is the goal of the present study to compare the predictions of the BEC dark matter models with the SPARC sample of high-quality rotation curves (Lelli, McGaugh and Schombert, 2016), and to search for the specific signatures of the presence of condensate dark matter. After performing several cuts to the sample, we keep a number of 139 galaxies, each modeled by a gaseous disc, a stellar disc, a dark matter halo, and a stellar bulge, if appropriate. For these models we apply a fitting technique based on genetic algorithms, and we obtain the physical parameters for each galaxy (central density, rotational velocity, and halo radius).
The present paper is organized as follows. In Section 2 we briefly present the basic properties of the static and rotating Bose-Einstein Condensatedark matter halos. The comparison of the theoretical predictions of the BEC model with the high quality rotation curves data of the SPARC sample is performed in Section 3. We discuss and conclude our results in Section 4.
2 Bose-Einstein Condensate Dark Matter Halos in Slow Rotation
In the following we assume that the dark matter halos consist of a strongly - coupled, but dilute bosonic Bose-Einstein Condensate at absolute zero temperature (Membrado, Pacheco and Sanudo, 1989). Therefore almost all dark matter particles must be in the condensate. In a cold and dilute fluid, only low energy binary collisions are important. These collisions can be described, independently of the details of the two-body potential, with the help of a single parameter, the s-wave scattering length . Hence, the interaction potential can be replaced with an effective interaction , with the coupling constant related to the scattering length through the relation . The ground state properties of the dark matter are described by the mean-field Gross-Pitaevskii (GP) equation, which for the case of rotating dark matter halos can be derived from the GP energy functional, which takes the form
| (3) | |||
| (4) |
where is the wave function of the condensate, and (Pethick and Smith, 2008). The first term in the GP energy functional is the quantum pressure, the second is the rotational energy , where is the angular velocity of the condensate, the third is the interaction energy, while the fourth term gives the gravitational potential energy. We also introduce the mass density of the condensate, defined as . The wave function obeys the normalization condition is , where is the total number of condensate dark matter particles. The variational procedure
| (5) |
gives the GP equation as (Boehmer and Harko, 2007)
| (6) |
where is the chemical potential. The gravitational potential satisfies the Poisson equation
| (7) |
In the case of the galactic dark matter halos the number of particles in the condensate is very large, and therefore the quantum pressure term makes a significant contribution only near the boundary of the galaxy. Moreover, it is much smaller than the interaction energy term. Thus for condensate galactic halos, the quantum pressure term can be neglected, and this approximation is called the Thomas-Fermi approximation. For a very large number of particles, when , the Thomas-Fermi approximation becomes exact (Pethick and Smith, 2008). Hence in this approximation we obtain
| (8) |
Then the Poisson equation gives the density profile of the dark matter halo as (Zhang et al., 2018)
| (9) |
where we have denoted
| (10) |
From a mathematical point of view Eq. (9) represents a Helmholtz type equation.
2.1 Static Bose-Einstein Condensate dark matter halos
In the case when the rotation of the condensate can be neglected, , the density distribution of the static gravitationally bounded dark matter Bose-Einstein condensate is obtained as (Boehmer and Harko, 2007)
| (11) |
where is the central density of the condensate, . The density profile has the important property of being non-singular at the galactic center . The mass profile of the galactic dark matter halo can be obtained as
| (12) |
with a boundary radius . At the boundary of the dark matter distribution we have , a condition that gives . Hence for the radius of the condensate dark matter halo we find the expression
| (13) |
The tangential velocity of a massive test particle in rotational notion in the condensed dark halo is obtained, in the Newtonian approximation, as
| (14) |
or, equivalently,
| (15) |
The total mass of the galactic dark matter halo is found to be
| (16) |
giving for the mean value of the condensate density the expression . Therefore the tangential velocity can also be represented as
| (17) |
For the rotation curves are given by the standard Keplerian law, with . The mass of the dark matter particle in the dark matter halo is given by
| (18) |
For fm and kpc, we obtain for the typical mass of the condensate particle a value of the order of meV. For fm, a value of the scattering length that corresponds to values of specific for laboratory experiments, eV. These values are consistent with the limit eV obtained for the mass of the condensate particle from cosmological considerations (Boyanovsky, de Vega and Sanchez, 2008).
2.2 Slowly rotating Bose-Einstein Condensate dark matter halos
In the analysis of the slowly rotating Bose-Einstein Condensate dark matter halos we follow the approach developed in (Zhang et al., 2018). The general solution of Eq. (9) can be obtained as (Zhang et al., 2018)
| (19) |
where by we have denoted the spherical Bessel functions, giving the solutions of the radial part of the equation. The solutions of the angular part of the Helmholtz equation are given by the Legendre polynomials . The integration constants must be determined from the condition of the continuity of the gravitational potential across the boundary of the galactic condensate dark matter halo. By assuming the condition
| (20) |
which corresponds to the physical case of a slow rotation of the dark matter halo, it turns out that the deviation from a spherically symmetric matter distribution can be considered small. Therefore in the slow rotation approximation we can use with a good approximation perturbative methods, by introducing the perturbation parameter .
The boundary of the dark matter halo is defined by the condition . In the first order of approximation we obtain for the density distribution the expression Zhang et al. (2018)
| (21) |
Alternatively, the density distribution of the dark matter in the BEC halo can be written as,
| (22) |
where we have denoted
| (23) |
The radius of the slowly rotating Bose-Einstein Condensate dark matter halo, defined as the radius where the dark matter density vanishes, can be computed according to the relation (Zhang et al., 2018)
| (24) |
The equatorial radius of the galactic dark matter halo can be obtained as
| (25) |
If we have , and hence we recover the static case. For slowly rotating dark matter halos the mass distribution inside radius is given by (Zhang et al., 2018)
| (26) |
Due to the presence of the rigid body type rotation, a second term appears in the mass profile, which is not present in the static case. In the first order of approximation the tangential velocity of massive test particles rotating in the Bose-Einstein Condensate galactic dark matter is given by
or, in an alternative representation, in terms of the radius of the static configuration, by 111This equation corrects Eq. (103) of reference (Zhang et al., 2018), where, due to a typing mistake, the term proportional to is missing in the definition of .,
| (28) |
The total mass of the galactic dark matter halo is defined according to (Zhang et al., 2018)
| (29) |
where is the radius of the galaxy.
In the first order of the total mass of the galactic condensate can be obtained as
| (30) |
The total halo mass of a given galaxy is fully determined by the evolutionary processes that led to its formation. The halo mass is not modified by the presence of rotation. But, as it follows from Eq. (30), the rotation of the halo allows the galaxy to have more mass than a static one. Thus the rotation of the dark matter halo becomes a stabilizing factor that prevents gravitational collapse.
The central density of the galaxy is determined by the total mass and angular velocity of the halo according to
| (31) |
The mean density of the rotating BEC halo is given by
| (32) |
where is the galactic volume. The mean density of the rotating dark matter distribution is smaller than the mean density of the static configuration.
3 Testing the Bose-Einstein Condensate dark matter model with the SPARC high resolution rotation curves
In the present Section we consider a comparison of the theoretical predictions of the Bose-Einstein Condensate dark energy model with the observations of the galactic rotation curves.
3.1 The SPARC sample and the fitting procedure
For the present study we use the rotation curves from the SPARC database (Lelli, McGaugh and Schombert, 2016). This sample consists of 175 high-quality HI/H rotation curves, together with accompanying 3.6m photometry from Spitzer. The SPARC sample contains a large variety of data, extending over 5 orders of magnitude in mass. It also encompasses a variety of morphologies. The considered 3.6 m surface brightness is a good tracer of the stellar mass, and hence its combination with rotation curve data allows detailed modelling of the different components of a given galaxy.
The SPARC database includes a large variety of information for each galaxy. From the point of view of the test of the BEC dark matter models the most important information is contained in , giving the rotation speed as a function of radial coordinate , together with the corresponding error bars. From the photometrical information one can also obtain the contributions to the rotation speed of the stellar disc and of the stellar bulge, and , respectively. The bulge component is included only for galaxies for which the photometry profile significantly differs from an exponential disc profile in the central regions. and are obtained by taking a mass-to-light ratio of 1 , and therefore these quantities must be rescaled for other ratios. For each galaxy, the information on the gas surface brightness was converted into a gas contribution to the total velocity .
The distribution of the number of galaxies according to their type in the SPARC sample is represented in Fig. 1.
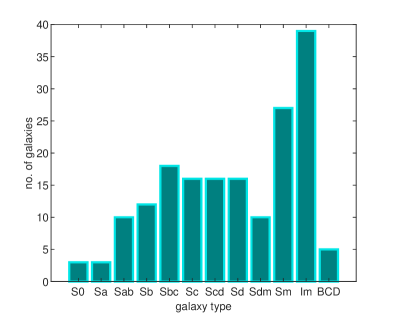
The histogram of lengths for the galactic velocities in the SPARC sample is represented in Fig. 2.

We have taken into account for the fits of the theoretical model only the data with length greater than or equal to 7.
In order to test the velocity of the massive particles in the Bose-Einstein Condensate dark matter halo defined by Eq. (2.2) we have fitted the total velocity from SPARC database with a total velocity , which also includes the baryonic matter contribution, and which is given by the relation
| (33) |
where and are the mass-to-light ratios for the stellar disc and the bulge, respectively. In order to determine the free parameters of the BEC model we have looked for the minimum of the function
| (34) |
where is the length of data and is the number of parameters that must be estimated, i.e, for bulgeless galaxies and for galaxies with bulge.
We have used the so-called genetic algorithms to find the parameters that minimizes the objective function (34) for a given set of constraints. The genetic algorithms that belongs to the larger class of evolutionary algorithms are inspired by the Darwinian process of natural selection (‘survival of the fittest’), and they are used to generate solutions to optimization problems by relying on biologically inspired operators such as mutation, crossover and selection.
In order to apply these algorithms one must define first a fitness function, which in the present case is the objective function defined by Eq. (34). Then we initialize the genetic algorithms by considering an initial population of random candidates for obtaining a solution, and we compute the fitness value for each candidate. Then new populations are iteratively generated by selection, crossover and mutation until the entire process is stopped when the average relative change in the fitness function value is less than .
The total population size values were considered in the range [4000,5000], while for the crossover fraction (the ratio from the population size that will be recombined for the next population) we have taken values in the interval [0.6,0.9]. For each galaxy we have adapted the initial population range. For the maximum number of generations we have adopted the value . In our investigation we have limited the values of and to the range [0.1,5]. We also require that the density of the halo must be a monotonically decreasing function of the radial coordinate in the range . On the rotation parameter we have imposed the constraint
| (35) |
For the lower bound for the central density of the dark matter halo we have adopted the value , while the lower bound for the static radius of the dark matter halo was set to .
3.2 Fitting results

The results of the fitting of the rotation curves of a set of 9 galaxies from the SPARC sample with the predictions of the slowly rotating BEC dark matter model are presented in Fig. 3. As one can see, the theoretical model fits well the observational data, despite the apparent complexity of the total rotation curves. For the considered galaxies only NGC1705 and NGC4088 do indicate the presence of flat rotation curves, extending for a large radius. They also show a clear evidence for the Keplerian profile of the baryonic matter distribution. For the other galaxies the baryonic contribution to the total velocity distribution is either increasing, or a constant, indicating a strong effect of the luminous matter on the rotation curves.
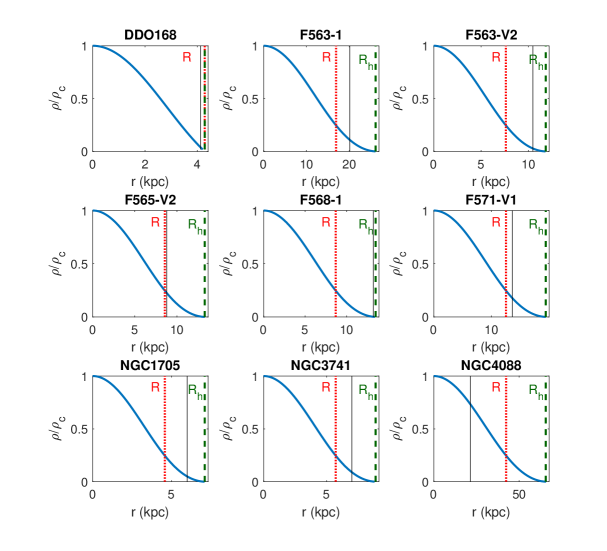
In Fig. 4 we have represented the density distribution of the dark matter halo for the galaxies whose rotation velocity curves are represented in Fig. 3. With vertical dotted, respectively dashed line we pointed the values of the estimated static and rotating radius of the dark matter halo , respectively , and with continuous line the maximum radius of observed data. For all considered cases the density of the BEC halo is a monotonically decreasing function of the radial coordinate , and it becomes zero for a fixed value of , which formally defines the radius of the halo. The presence of a well-defined boundary is one of the important characteristics of the BEC dark matter models, and of their density profiles, clearly indicating a finite physical size of the dark matter halo.
| Galaxy | ||||||
| (kpc) | (kpc) | |||||
| DDO168 | 4.281 | 4.281 | 1.608 | 0.000 | 0.100 | 2.610 |
| F563-1 | 16.902 | 26.298 | 0.315 | 1.203 | 4.446 | 1.151 |
| F563-V2 | 7.619 | 11.854 | 1.002 | 2.147 | 4.047 | 0.111 |
| F565-V2 | 8.567 | 13.329 | 0.715 | 1.814 | 1.575 | 0.194 |
| F568-1 | 8.691 | 13.522 | 1.323 | 2.467 | 2.637 | 0.540 |
| F571-V1 | 12.521 | 19.481 | 0.319 | 1.211 | 1.561 | 0.176 |
| NGC1705 | 4.577 | 7.120 | 1.885 | 2.945 | 2.416 | 0.455 |
| NGC3741 | 5.720 | 8.899 | 0.703 | 1.798 | 2.109 | 1.310 |
| NGC4088 | 42.376 | 65.932 | 0.174 | 0.894 | 0.445 | 0.563 |
The physical parameters of the BEC dark matter halos as obtained from the fitting of the galaxies presented in Fig. 3 are represented in Table 1. The obtained results predict that the central density of the dark matter distribution is of the order of g/cm3, while their rotational velocities is of the order of s-1. One should also point out that some fitting results indicate the presence of static (nonrotating) galaxies, like, for example, DDO168. This raises the question if indeed all BEC galaxies are rotating, and, if not, of the physical/astrophysical processes that could lead to a global galactic dynamics.
4 Discussions and final remarks
In the present work, we have considered the potential observational signatures of the Bose-Einstein Condensate dark matter model in the high-quality HI/H measurements of the rotation curves of the SPARC data. After reconsidering the data of the sample, and excluding all galaxies with a low number of measurements, we have considered in our analysis only 139 of the original 175 galaxies. The galaxies in the SPARC database are modelled as containing a stellar disc, a gaseous disc, a dark matter halo, and (where appropriate) a stellar bulge. Then, we have fitted the data on the rotational velocities with Eq. (2.2), giving the expression of the tangential velocity of massive test particles in the Bose-Einstein Condensate dark matter model. The tangential velocity is fixed in terms of three quantities only: the central density of the halo, the rotation angular velocity of the dark matter distribution, and the radius of the static configuration.
The main findings of our analysis are as follows:
-
•
The slowly rotating Bose-Einstein Condensate dark matter model obtained gives good results in the fitting of the data of the SPARC sample. The values of the objective function are smaller than for 61 galaxies with data length greater than or equal to and reasonable values of the optimal parameters. The distribution of the values of the objective function for is represented in Fig. 5
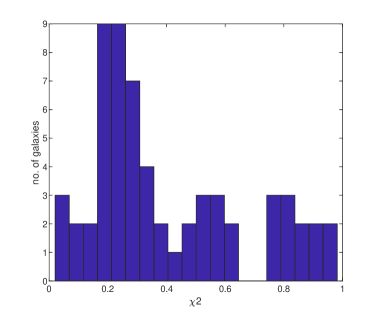
Figure 5: The histogram of the values of the objective function -
•
The density distribution of the BEC dark matter is nonsingular at the galactic center, and it shows a clear cored central profile. It has been already suggested (Harko, 2011) that the condensation of dark matter can solve the core-cusp problem, and hence remove the unphysical features that appear in the Navarro-Frenk-White, CDM type, density profile. Our results based on the SPARC sample clearly indicate the presence of a core at the galactic center, a result which is supported by the astronomical observations.
-
•
Our results indicate a wide range of variations of the angular velocity of the galactic halo. Fig. 6 shows the distribution of the estimated values of the angular velocity . However, for a large number of galaxies the angular velocity turns out to be very close to zero, indicating the static nature of the condensate dark matter halo. This raises the interesting question of the nature, origin and dynamics of the galactic rotation of dark matter, and of its dissipation for certain structures. Is the galactic rotation the result of some perturbations in the late evolutionary periods, or it is an intrinsic property that could be related to the initial collapsing phases?
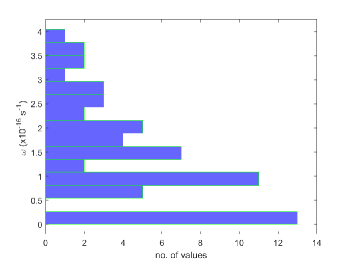
Figure 6: The distribution of the estimated values of the angular velocity . -
•
Another fitting parameter, the central density of the condensate dark halo, has also been obtained from our analysis. The distribution of the estimated values of central density is represented in Fig. 7. Even that obtaining the central density of dark matter at the galactic center may prove to be an extremely difficult observational task, the central density distribution of dark matter may provide, at least in principle, a specific signature that may help in discriminating BEC dark matter models from other models.

Figure 7: The distribution of the estimated values of central density . -
•
The third fundamental parameter determining the structure and properties of the condensate dark matter halos is the radius of the static configuration, which is fully determined by the two fundamental physical parameters of the dark matter, the mass of the dark matter particle, and by its scattering length. Hence should have a universal value in all condensate dark matter models. From our investigation it follows that is well constrained by the SPARC observational data, but the spread of the obtained values of across the sample is very broad, spanning roughly one order of magnitude. This result seems to be inconsistent with the existence of a single universal value for . The BEC dark matter models make a very definite prediction about the existence of a finite, and well defined radius of the dark matter distribution. The determination of in our investigation is determined by the spatial extension of the analyzed sample, and by the fact that the value of is strongly correlated by the maximum value of from the observational data. In Fig. 8 we have represented the estimated values of the radius of the static dark matter configuration with respect to , for the galaxies for which we obtained . These two quantities are strongly correlated, with the Pearson correlation coefficient given by .
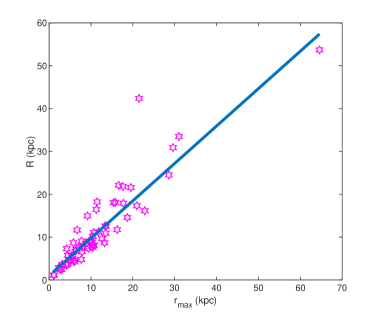
Figure 8: The values of the estimated static radius of the condensate dark matter halo versus . Presently there are no convincing data indicating the existence of a given radius of the galactic dark matter halo, and of its universal nature. In several dark matter models the dark matter distribution extends to infinity. However, if a future detection of the radii of a large sample of galactic objects would be possible, this would allow a definite test of the BEC dark matter model. An observational proof of the infinite extension of the galactic halos would certainly contradict one of the basic predictions of the BEC model.
The existence of BEC dark matter in nature depends essentially on the significant increase in the number of observational data, and of their precision. A universal length scale, determined by the physical properties of the dark matter particle, is one of the main predictions of the theory. On the other hand the outcome of the core/cusp debate may also provide evidence for BEC dark matter. If simulations done in the framework of the CDM model with baryonic effects included could predict cored profiles, then the presence of galactic halos made of BEC may not be necessary. If, on the other hand, the results of the simulations would still indicate cuspy NFW-like galactic halo profiles, then the BEC dark matter model may provide a realistic explanation for the cored profiles observed in a large number of galaxies.
Acknowledgments
We would like to thank Prof. László Gergely for comments and suggestions that helped us to improve our manuscript. T. H. thanks the Yat Sen School of the Sun Yat-Sen University in Guangzhou, P. R. China, for the kind hospitality offered during the preparation of this work.
References
- Ade et al. (2016) Ade, P. A. R. et al., Planck Collaboration: 2016, Astron. Astrophys. 594, A1.
- Anderson et al. (1995) Anderson, M. H., Ensher, J. R., Matthews, M. R., Wieman, C. E., Cornell, E. A.: 1995, Science 269, 198.
- Boehmer and Harko (2007) Boehmer, C. G., Harko, T.: 2007, JCAP 06, 025.
- Boyanovsky, de Vega and Sanchez (2008) Boyanovsky, D., de Vega H. J., Sanchez, N.: 2008, Phys. Rev. D 77, 043518.
- Boylan-Kolchin, Bullock and Kaplinghat (2011) Boylan-Kolchin, M., Bullock, J. S., Kaplinghat, M.: 2011, Mon. Not. Roy. Astron. Soc. 415, L40.
- Bradley et al. (1995) Bradley, C. C., Sackett, C. A., Tollett, J. J., Hulet, R. G.: 1995, Phys. Rev. Lett. 75, 1687.
- Bull et al. (2016) Bull, P., et al.: 2016, Physics of the Dark Universe, 12, 56.
- Bullock and Boylan-Kolchin (2017) Bullock, J. S., Boylan-Kolchin, M.: 2017, Annual Review of Astronomy and Astrophysics 55, 343.
- Davis et al. (1995) Davis, K. B., Mewes, M. O., Andrews, M. R., van Drutten, N. J., Durfee, D. S., Kurn, D. M., Ketterle, W.: 1995, Phys. Rev. Lett. 75, 3969.
- Di Cintio et al. (2014) Di Cintio, A., Brook, C. B., Dutton, A. A., Maccio, A. V., Stinson, G. S., Knebe, A.: 2014, Mon. Not. Roy. Astron. Soc. 441, 2986.
- Harko (2011) Harko, T.: 2011, JCAP 1105, 022.
- Harko et al. (2015) Harko T., Liang P.-X, Liang S.-D., Mocanu G.: 2015, JCAP 11, 027.
- Klypin et al. (1999) Klypin, A., Kravtsov, A. V., Valenzuela, O., Prada, F.: 1999, Astrophys. J. 522, 82.
- Lelli, McGaugh and Schombert (2016) Lelli, F., McGaugh, S. S., Schombert, J. M.: 2016, Astronom. J. 152, 157.
- Membrado, Pacheco and Sanudo (1989) Membrado, M., Pacheco, A. F. and Sanudo, J. S.: 1989, Astron. Astrophys. 217, 92.
- Moore et al. (1999) Moore, B., Ghigna, S., Governato, F., Lake, G., Quinn, T., Stadel, J., Tozzi, P.: 1999, Astrophys. J. 524, L19.
- Navarro, Frenk and White (1997) Navarro, J. F., Frenk, C. S., White, S. D. M.: 1997, Astrophys. J. 490, 493
- Oh et al. (2015) Oh, S.-H., et al.: 2015, Astronom. J. 149, 180.
- Pethick and Smith (2008) Pethick, C. J. and Smith, H.: 2008, Bose-Einstein condensation in dilute gases, Cambridge, Cambridge University Press.
- Zhang et al. (2018) Zhang, X., Chan, M. H., Harko, T., Liang, S.-D., Leung, C. S.: 2018, EPJC 78, 346.
not available yet
