Abstract
An elliptic one-dimensional second order boundary value problem involving discontinuous coefficients, with or without transmission conditions, is considered. For the former case by a direct sum spaces method we show that the eigenvalues are real, geometrically simple and the eigenfunctions are orthogonal.
Then the eigenpairs are computed numerically by a local linear finite element method (FEM) and by some global spectral collocation methods.
The spectral collocation is based on Chebyshev polynomials (ChC) for problems on bounded intervals respectively on Fourier system (FsC) for periodic problems.
The numerical stability in computing eigenvalues is investigated by estimating their (relative) drift with respect to the order of approximation. The accuracy in computing the eigenvectors is addressed by estimating their departure from orthogonality as well as by the asymptotic order of convergence. The discontinuity of coefficients in the problems at hand reduces the exponential order of convergence, usual for any well designed spectral algorithm, to an algebraic one.
As expected, the accuracy of ChC outcomes overpasses by far that of FEM outcomes.
Authors
Tiberiu Popoviciu Institute of Numerical Analysis
School of Mathematics, University of the Witwatersrand, Johannesburg, South Africa
Keywords
References
See the expanding block below.
Paper coordinates
C.I. Gheorghiu, B. Zinsou, Analytic vs. numerical solutions to a Sturm-Liouville transmission eigenproblem, J. Numer. Anal. Approx. Theory, 48 (2019) no. 2, 159-174. Retrieved from https://ictp.acad.ro/jnaat/journal/article/view/1201
About this paper
Journal
J. Numer. Anal. Approx. Theory
Publisher Name
Editura Academiei Romane
DOI
not available yet.
Print ISSN
2457-6794
Online ISSN
2501-059X
Google Scholar Profile
soon
Paper (preprint) in HTML form
Analytic vs. Numerical Solutions to a Sturm-Liouville Transmission Eigenproblem
Abstract.
An elliptic one-dimensional second order boundary value problem involving discontinuous coefficients, with or without transmission conditions, is considered. For the former case by a direct sum spaces method we show that the eigenvalues are real, geometrically simple and the eigenfunctions are orthogonal.
Then the eigenpairs are computed numerically by a local linear finite element method (FEM) and by some global spectral collocation methods. The spectral collocation is based on Chebyshev polynomials (ChC) for problems on bounded intervals respectively on Fourier system (FsC) for periodic problems. The numerical stability in computing eigenvalues is investigated by estimating their (relative) drift with respect to the order of approximation. The accuracy in computing the eigenvectors is addressed by estimating their departure from orthogonality as well as by the asymptotic order of convergence. The discontinuity of coefficients in the problems at hand reduces the exponential order of convergence, usual for any well designed spectral algorithm, to an algebraic one. As expected, the accuracy of ChC outcomes overpasses by far that of FEM outcomes.
Key words and phrases:
Sturm-Liouville eigenproblem, discontinuous coefficient, transmission condition, FEM, spectral collocation, accuracy1991 Mathematics Subject Classification:
47A10, 65L15, 65L20, 65L60, 65L70Str. Fântânele 57, 400320 Cluj-Napoca, Romania, e-mail: ghcalin@ictp.acad.ro.
1. Introduction
The aim of this paper is twofold. We investigate analytically as well as numerically an elliptic one-dimensional second order eigenvalue problem with interior transmission conditions. The problem is a Dirichlet one, self-adjoint, involving a discontinuous coefficient. Thus we first show that eigenvalues are real and geometrically simple and the eigenvectors are orthogonal.
Then, using the FEM with linear test and trial bases (the so called linear hat functions), we find out the whole spectrum of the problem i.e. the set of all eigenpairs (eigenvalues and eigenvectors). The method is local and produces some generalised eigenvalue problems (GEP) containing pencils of sparse (tridiagonal) and possibly symmetric matrices. We also investigate the accuracy of numerical eigenpairs. The accuracy of the first (smallest) eigenvalues is estimated by computing their relative drift with respect to the order of approximation as well as with respect to the physical parameter involved in the definition of transmission conditions. As we could not find in literature numerical result for the problem at hand, we have tried to back them by some results obtained using a higher order method. Thus we use a collocation method based in Chebyshev polynomials. This is a very efficient global method which works equally well when the transmission conditions are not taken into account. In order to show robustness of spectral collocation, we solve an additional periodic SL problem with divergence coefficient exhibiting two discontinuities. This time periodicity requires a spectral collocation based on classical Fourier system (FsC).
Whenever the coefficient in the divergence form of the problem is continuous, the spectral method fairly works, i.e., the eigenvalues are obtained close to the machine precision (32 digits) and the convergence in computing eigenvectors is super-geometric. Due to the discontinuity of divergence coefficient, this convergence reduces to an algebraic one.
Actually we observe that our numerical results are in accordance with the theoretical (analytic) ones. Moreover, we try to make them more precise, for instance, to observe to what extent the discontinuity of coefficients influences the smoothness of eigenmodes.
Differential equations of the elliptic type involving discontinuous coefficients arise in many fields of science and engineering (see for instance [6], [10], [13], [21] and [22] to quote but a few). For example, they model the dependence of the electrostatic potential on the electric charge in a conductor. They also model static deformation in elastic solids. The coefficients appearing in the equations are material parameters. Real materials are often composite and the material parameters then exhibit jumps across internal surfaces. These surfaces are often called interfaces. When interfaces are present, solutions to the PDEs must satisfy extra conditions, called transmission conditions. The presence of jumps at interior interfaces can cause scattering of waves, such as in a vibrating string made of two different types of materials. Transmission problems arise often in optics as well as various physics and electrical engineering problems.
Studying PDEs with jumps in the coefficients are challenging and the corresponding numerical methods used to solve them are more complex, than in the case of continuous coefficients (see for instance [2]). We solve in this paper a model transmission problem in one dimension on a finite interval, imposing Dirichlet boundary conditions at the ends of the interval, as well as a periodic Sturm-Liouville problem involving discontinuous coefficients.
We can trace back the direct sum spaces method to the old paper of Zettl [24] as well as to a more recent paper [9]. We are perfectly conscious that in spite of the fact that the divergence coefficient is discontinuous its inverse is locally integrable and thus the classical theory of existence for Sturm-Liouville eigenproblem is applicable (see for instance the Pryce’s monograph [20] and that of Zettl [25]). Using the above mentioned method, we want to open another perspective for the class of problems at hand.
In [1] (see also [17]) Aydemir and Mukhtarov investigate various qualitative properties of eigenvalues and corresponding eigenfunctions of a Sturm-Liouville problem with an interior singular point. They introduce a special Hilbert space along with a Rayleigh-Ritz formulation. We will introduce in Section 3 a slightly more general and useful weak formulation than this Rayleigh-Ritz formulation. However, Yserentant in [26] shows that for such formulation the computed eigenvalues as well as the corresponding eigenvectors converge to their continuous counterparts.
The organisation of the paper is as follows: In Section 2, we find out the most important analytic results concerning the eigenvalue problem at hand. In Section 3, we provide the weak (variational) formulation of the second order elliptic eigenproblem with transmission conditions. In Section 4, we summarise the simplex FEM as well as ChC for our problem. In Section 5, we provide the extensive numerical results obtained, i.e., the set of the first six eigenvalues and of the first six eigenvectors. We also advocate on the accuracy of our outcomes and comment on the dependence of the spectrum on the magnitude of jump. In addition, we solve a periodic eigenproblem with discontinuous coefficients in Subsection 5.1 using FsC. Consequently we observe that both spectral schemes, ChC as well as FsC, can be some serious competitors for the well established codes devoted to the eigenvalue problems. Section 6, ends up the paper with some conclusions and open problems.
2. Eigenvalues and eigenfunctions
We consider the Sturm-Liouville (SL) equation,
| (1) |
where
With the differential equation (1), we consider the boundary conditions
| (2) | ||||
| (3) |
together with the transmission conditions
| (4) | ||||
| (5) |
The Hilbert spaces and are the spaces of all classes of complex-valued measurable functions and such that
Define
| (6) |
and the inner product
| (7) |
for all . Then is a Hilbert space with respect to the inner product (7).
Lemma 1.
Proof.
Proof.
Remark 3.
Let be an eigenvalue of the problem (1)–(5) with corresponding eigenfunction , where and are real-valued functions. Then both and are also eigenfunctions corresponding to the same eigenvalue . Indeed, putting and in (1)–(5), we get
Hence both and are eigenfunctions corresponding to the same eigen- value .
Proof.
Assume that there exist two linearly independent eigenfunctions and for the same eigenvalue . The boundary condition (2) implies that . Thus for all . Since and are solutions of (1), then there exists such that for all . Similarly, it follows from the boundary condition (2), that there exists such that for all . Hence
| (11) |
Substituting (11) in the transmission conditions (4)–(5), we get
| (12) | |||
| (13) |
It follows that . Therefore and are linearly dependent on . This completes the proof.∎
Remark 5.
Note that the eigenfunctions of the problem (1)–(5) can be chosen to be real-valued. Indeed, let be an eigenvalue with the eigenfunction . By Remark 3 and are also eigenfunctions corresponding to the same eigenvalue . By Theorem 4, there exists a complex number such that . Hence , i.e. there is only one real-valued eigenfunction, except for a constant factor, corresponding to each eigenvalue. From now we can assume that all eigenfunctions of the problem (1)–(5) are real-valued. ∎
3. Variational (weak) formulation
From the definition of coefficient (see Section 2) there exists a positive constant such that i.e., the problem is elliptic. To justify the transmission conditions, we begin with the so-called weak formulation of the problem (1)–(3), namely:
| (14) |
Such formulations for elliptic problems are the starting point for the most modern numerical methods (see the classic texts of Brenner and Scott [7] or Ciarlet [8]).
In order to obtain the equation (14), in the unknown , we multiply the equation (1) with another suitable function , called a test function, and then integrate over . Thus we simply have
| (15) |
The function is chosen to satisfy the same Dirichlet boundary conditions as , namely:
so that there are no extra terms coming from the integration by parts.
Then, we split up the integral on the left hand side of (15), given that has a jump at and get
| (16) |
This allows us to have continuous functions in each integrand. We can then integrate by parts each integral, obtaining the following:
| (17) |
We can see given the boundary conditions that and similarly will vanish. In order to obtain the weak formulation (14), we need to impose some conditions at the jump site . More exactly we must apply first the continuity of the solution at this site. Thus, we need to enforce the transmission condition (4). Hence we have to impose just the transmission condition for the first derivative (5). Thus, we obtain (14) which is the weak formulation of the transmission eigenproblem (1)–(5). However, in this formulation the coefficient is not differentiated and the integral is well defined as long as the test (shape) function and the trial function are differentiable in some sense.
The formal variational (weak) formulation (14) now reads:
Find and such that
| (18) |
4. The Simplex FEM and ChC
Let now be the space of polynomials of degree at most . We define the space of piecewise linear polynomial functions
| (19) |
We will use the FEM in its simplest form, i.e., simplex where the basis for test as well as trial functions, contains only piecewise linear functions, the so called linear hat functions. All these functions belong to the above defined space .
In order to define these functions we start by partitioning the interval into equal subintervals, where is a positive integer called the approximation order. This gives rise to nodes of the form . Later on, we will choose for some integer , so that is a node and the jump in the coefficient occurs at that node. This simplifies our analysis as we discuss more later on.
For each we construct a hat function as follows. Each is a hat function of height , which is non zero and piecewise linear on the interval . Thus,
| (20) |
and its derivative reads
We will seek a solution to our problem (16) in the form:
| (21) |
The stiffness matrix has the entries
and thus it is a tridiagonal one.
The mass matrix is defined by the entries
This matrix is also tridiagonal and additionally symmetric. Thus, the non zero entries in the stiffness matrix and in the mass matrix have the following numerical values:
and
We plug in the computed entries and to get the following sparse GEP
| (22) |
Being sparse and tridiagonal, both matrices in GEP (22) can be efficiently implemented in MATLAB using the routine diag.
The analytic results from Sect. 2 and Sect. 3 concerning the continuity of , i.e., enable us to use alternatively the strong ChC method in order to solve the SL transmission problem. Thus in the finite dimensional representation of solution in (21) instead of linear hat functions we use the Chebyshev polynomials (see for instance our text [12] and the seminal paper [23]).
Thus, we have to find out the eigenpairs of the matrix
| (23) |
the vector contains Chebyshev nodes of the second kind and the dimensional vector is defined as
The matrix is the Chebyshev collocation differentiation matrix on the above Chebyshev nodes (see [23] for its implementation). Actually we search the eigenvalues of
as we have enforced the homogeneous Dirichlet boundary conditions. The MATLAB code eig and another real variant of the Jacobi-Davidson method (see our contribution [11]) are used consecutively in order to mutually confirm the numerical values obtained. We have to mention that the matrix
is fully populated and rather non normal. Its Henrici’s number equals
For the importance of non normality and its numerical measure provided by Henrici’s number in context of eigenvalue problems we refer to our contribution [12].
5. Numerical results
A banded FEM (Galerkin) discretization matrix saves us nothing over a dense matrix in pseudospectral method if the linear algebra is to be handed off by QZ (QR) algorithm. Its main drawback is the cost. Because it uses iteration, rather than a finite set of steps, a precise estimate of cost is impossible but experience has shown that the QZ cost is floating point operations. Alternatively, we use the MATLAB built in eigs which takes into account the sparsity of matrices in (22) and finds out the left column in Table 1.
| by FEM | by ChC | |
|---|---|---|
For a specified eigenvalue the relative drift is defined by J. P. Boyd in [5] with the quotient
| (24) |
where and are two distinct orders of approximation. The relative drift for the first eigenvalues computed by FEM and by ChC is displayed in Fig. 1 panels A) and respectively B).
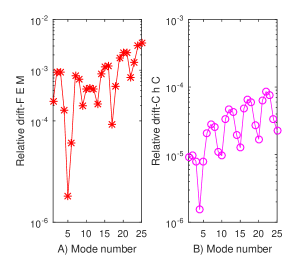
It signifies a reasonable numerical stability of computing eigenvalue process in FEM case and an excellent stability in case of ChC.
Fairly interesting is also the relative drift of eigenvalues with respect to the exact ones, i.e., when . In this case, we know that the exact eigenvalues of (1)–(3) are , . The drift in this case is depicted in Fig. 2. It is clear from panel B) of Fig. 2 that ChC computes the first few eigenvalues close to the machine precision.
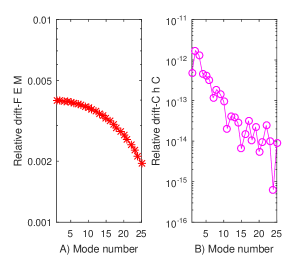
Moreover, using a multi-precision computing toolbox [15], our numerical experiments show that the accuracy of ChC increases with the number of digits in multi-precision approximation. As it is apparent from panel A) of Fig. 2 for FEM, this does not happen.
Actually, working with digits precision the first eigenvalue is computed by FEM with an accuracy better that .
It is also interesting to observe the asymptotic behaviour of the computed eigenvalues. In the Zettl’s monograph [25, p. 73], it is known that
When we try to verify this statement we get Fig. 3.
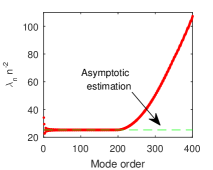
This picture confirms the Boyd’s RULE-of-THUMB for eigenvalues, i.e., for a spectral method using terms the lowest eigenvalues are usually accurate within a few percent while the larger are useless (see [5], p.132).
Fortunately, but less expectantly, a fairly similar conclusion holds for the set of eigenvalues computed by FEM.
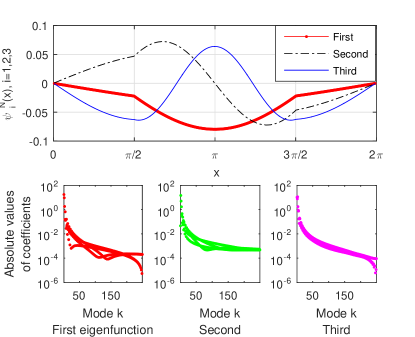
The first six eigenmodes computed by ChC are displayed in Fig. 4. We observe that they are continuous at the transmission point but their derivatives are not.
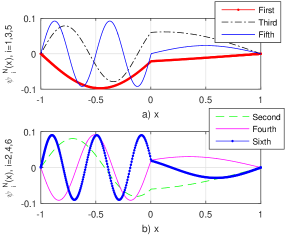
In order to evaluate the asymptotic order of convergence of ChC method in computing eigenmodes, we use the fast Chebyshev transform. Thus, we get the coefficients of Chebyshev expansion and then plot their absolute values in a log-linear plot. The behaviour of these coefficients for the first four vectors is depicted in Fig. 5. Using the strategy from Boyd [5] we can imagine the so called envelope, i.e., a curve which bounds these coefficient from above. This indicates an algebraic convergence, i.e., the coefficients satisfy for large .

As we compute a large set of eigenfunctions, Corollary 6 from Sect. 2 provides us an excellent tool to assess the accuracy in their computing. Thus, in order to measure the departure from orthogonality of the computed eigenmodes in a log-linear plot, we depict the numerical values of discrete scalar product of eigenvectors, namely
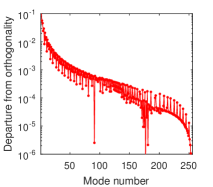
5.1. SL problem with discontinuous coefficients
In order to underline the versatility of spectral collocation methods we briefly compute the eigenspectrum of a SL problem with discontinuous coefficients from the paper of Babus̆ka and Osborn [2]. They consider a periodic boundary value problem attached to equation (1) when the divergence coefficient is measurable. The problem is factorised and a variational formulation is used. Some convergence results and error estimates for a mixed FEM are derived. These error estimates are based on the application of Sobolev spaces with variable constant order. Unfortunately no numerical results are provided.
However, the coefficient is defined by
| (25) |
We solve this periodic problem by Fourier collocation. It means that we have to use for the discretization the first order Fourier collocation differentiation matrix on the equispaced nodes
(see again [23] Sect. 3.5). This differentiation matrix is now a circulant one and thus normal. The first six eigenvalues are displayed in Table 2.
| computed by FC | |
|---|---|
We did not find similar results in the literature in order to validate the ones in the Table 2.
In order to evaluate the asymptotic order of convergence of FC method in computing eigenmodes, we use the discrete FFT (fft from MATLAB). Thus, we find out the coefficients of Fourier expansions. A fairly similar analysis with that for ChC method shows the same order of convergence, i.e. algebraic (see lower panels in Fig. 7).
It is worth noting at this moment that in [2] the authors solve only theoretically this problem and prove that the rate of convergence in approximation by FEM based on trigonometric polynomials is of order and this estimate cannot, in general, be improved. Our numerical outcomes reported in the lower panels of Fig. 7 confirm this statement.
Eventually, we have to observe that the sets of numerical eigenvalues computed by FEM, as well as spectral collocation methods, satisfy by far the estimations for lower bounds provided in [14].
6. Brief conclusions and some open problems
On completely different analytical considerations than the classical ones, we have proved three essential properties for the SL transmission eigenproblem, namely: all the eigenvalues of the problem are real, each eigenvalue is geometrically simple and eigenfunctions corresponding to distinct eigenvalues are orthogonal. To solve the problem numerically we have resorted to two distinct methods. The results obtained with their help are reasonably mutually closed. Additionally we remark that the global ChC method is by far much more precise than FEM despite the fact that it is based on full populated and non normal matrices compared to the sparse (even symmetric) matrices produced by the FEM.
It is also important to underline that the global collocation method operates without considering the transmission conditions. It is robust, efficient and easy to extend to higher-order problems.
The Fourier collocation worked with the same convergence order for a periodic problem. Last but not least important, both spectral collocation methods offer challenging alternatives for older codes devoted to solve various SL problems (see for instance [3], [4] and [19]). Finally, we must also note the reciprocal confirmation of the analytical and numerical outcomes.
References
-
[1]
K. Aydemir, O.S. Mukhtarov, Qualitative analysis of eigenvalues and
eigenfunctions of one boundary value-transmission problem, Bound. Value Probl., 82 (2016).
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
-
[2]
I. Babus̆ka, J.E. Osborn, Numerical treatment of eigenvalue problems for
differential equations with discontinuous coefficients, Math. Comp., 32 (1978), pp. 991–1023.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
-
[3]
P.B. Bailey, M.K. Gordon, L.F. Shampine, Automatic solution of the Sturm-Liouville problem,
ACM. T. Math. Software, 4 (1978), pp. 193–208.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
-
[4]
P.B. Bailey, W.N. Everitt, A. Zettl, Algorithm 810: the SLEIGN2 Sturm-Liouville code,
ACM T. Math. Software. 27 (2001) pp. 143–192.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
- [5] J.P. Boyd, Chebyshev and Fourier spectral methods, 2nd rev. ed. Mineola, NY: Dover Publications. 2001.
-
[6]
P.A.M. Boomkamp, B.J. Boersma, R.H.M. Miesen, G.V. Beijnon, A Chebyshev collocation method for solving two-phase
flow stability problems, J. Comput. Phys., 132 (1997), pp. 191–200.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
- [7] S.C. Brenner, L.R. Scott, The Mathematical Theory of Finite Element Methods, 3rd ed. Texts in Applied Mathematics 15. New-York, NY: Springer 2008.
- [8] P.G. Ciarlet, The Finite Element Method for Elliptic Problems, North-Holland, Amsterdam, New-York, Oxford, 1978.
-
[9]
W.N. Everitt, A. Zettl, Sturm–Liouville differential operators in direct sum spaces,
Rocky Mountain J. Math., 16 (1986), pp. 497–516.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
-
[10]
F. Gesztesyt, C. Macdeo, L. Streit, An exactly solvable periodic Schrodinger operator,
J. Phys. A: Math. Gen., 18 (1985), pp. L503–L507.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
-
[11]
C.I. Gheorghiu, J. Rommes, Application of the Jacobi-Davidson method to accurate analysis of singular linear
hydrodynamic stability problems, Int. J. Numer. Meth. Fl., 71 (2012), pp. 358–369.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
- [12] C.I. Gheorghiu, Spectral Methods for Non-Standard Eigenvalue Problems. Fluid and Structural Mechanics and Beyond, Springer Cham Heidelberg New York Dondrecht London, 2014.
-
[13]
Y. He, D.P. Nicholls, J. Shen, An efficient and stable spectral method for electromagnetic scattering
from a layered periodic sructure, J. Comput. Phys., 231 (2012), pp. 3007–3022.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
-
[14]
C.O. Horgan, J.P. Spence, A.N. Andry,
Lower bounds for eigenvalues of Sturm-Liouville problems with discontinuous coefficients: integral equation methods, Q. Appl. Math., 39 (1982), pp. 455–456.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
-
[15]
Multi-precision Computing Toolbox for MATLAB. Yokohama: Advanpix LLC.; 2008-2017.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
-
[16]
M. Marletta, J.D. Pryce, Automatic solution of Sturm-Liouville
problems using the Pruess method, J. Comput. Appl. Math., 39 (1992), pp. 57–78.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
-
[17]
O.S. Mukhtarov, M. Kadakal, F.S. Muhtarov, On discontinuous Sturm-Liouville problems
with transmission conditions, J. Math. Kyoto Univ. (JMKYAZ),
44 (2004), pp. 779–798.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
- [18] J. Nec̆as, Direct Methods in the Theory of Elliptic Equations, Springer Monographs in Mathematics, Berlin, 2012.
-
[19]
S. Pruess, C.T. Fulton, Mathematical Software for Sturm-Liouville
Problems, ACM T. Math. Software, 19 (1993), pp. 360–376.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
- [20] J.D. Pryce, Numerical solutions of Sturm-Liouville problem, Oxford University Press, Oxford, U. K., 1993.
- [21] D.G. Shepelsky, The inverse problem of reconstruction of the medium’s conductivity in a class of discontinuous and increasing functions, Adv. Soviet Math., 19 (1994), pp. 209–231.
-
[22]
I. Titeux, Ya. Yakubov, Completeness of root functions for thermal conduction
in a strip with piecewise continuous coefficients, Math. Models Methods
Appl. Sc., 7 (1997), pp. 1035–1050.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
-
[23]
J.A.C. Weideman, S.C. Reddy, A MATLAB Differentiation Matrix Suite, ACM T. Math. Software.
26 (2000), pp. 465–519.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
-
[24]
A. Zettl, Adjoint and self-adjoint boundary value problems with interface conditions, SIAM J. Appl. Math.,
16 (1968), pp. 851–859.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
- [25] A. Zettl, Sturm-Liouville Theory, Math. Surveys Monogr., vol. 121, Amer. Math. Soc., Providence, RI 2005.
-
[26]
H. Yserentant, A short theory of the Rayleigh-Ritz method, C.M.A.M. 13 (2013) pp. 496–502.
![[Uncaptioned image]](https://ictp.acad.ro/wp-content/uploads/2024/05/2019-Gheorghiu-JNAAT-ext-link.png)
[1] K. Aydemir and O.S. Mukhtarov, Qualitative analysis of eigenvalues and eigenfunctions of one boundary value-transmission problem, Bound. Value Probl. 82 (2016).
[2] I. Babuska and J.E. Osborn, Numerical Treatment of Eigenvalue Problems for Differential Equations with Discontinuous Coefficients, Math. Comput. 32 (1978), pp. 991–1023, DOI: 10.2307/2006330
[3] P.B. Bailey, M.K. Gordon and L.F. Shampine, Automatic Solution of the Sturm-Liouville Problem, ACM. T. Math. Software. 4 (1978), pp. 193–208, https://doi.org/10.1016/0377-0427(92)90222-J
[4] P.B. Bailey, W.N. Everitt and A. Zettl, Algorithm 810: The SLEIGN2 Sturm-Liouville Code, ACM T. Math. Software. 27 (2001) pp. 143–192, https://doi.org/10.1145/383738.383739
[5] J.P. Boyd, Chebyshev and Fourier spectral methods, 2nd rev. ed. Mineola, NY: Dover Publications. 2001.
[6] P.A.M. Boomkamp, B.J. Boersma, R.H.M. Miesen and G.V. Beijnon, A Chebyshev Collocation Method for Solving Two-Phase Flow Stability Problems, J. Comput. Phys. 132 (1997), pp. 191–200, https://doi.org/10.1006/jcph.1996.5571
[7] S.C. Brenner, L.R. Scott, The mathematical theory of finite element methods, 3rd ed. Texts in Applied Mathematics 15. New-York, NY: Springer 2008, https://doi.org/10.1007/978-0-387-75934-0
[8] P.G. Ciarlet, The Finite Element Method for Elliptic Problems, North-Holland, Amsterdam, New-York, Oxford 1978.
[9] W.N. Everitt, A. Zettl, Sturm–Liouville differential operators in direct sum spaces, Rocky Mountain J. Math. 16 (1986), pp. 497–516, https://doi.org/10.1216/rmj-1986-16-3-497
[10] F. Gesztesyt, C. Macdeo and L. Streit, An exactly solvable periodic Schrodinger operator J. Phys. A: Math. Gen. 18 (1985), pp. L503–L507, https://doi.org/10.1088/0305-4470/18/9/003
[11] C. I. Gheorghiu, J. Rommes, Application of the Jacobi-Davidson method to accurate analysis of singular linear hydrodynamic stability problems, Int. J. Numer. Meth. Fl. 71 (2012), pp. 358–369, https://doi.org/10.1002/fld.3669
[12] C.I. Gheorghiu, Spectral Methods for Non-Standard Eigenvalue Problems. Fluid and Structural Mechanics and Beyond, Springer Cham Heidelberg New York Dondrecht London 2014, https://doi.org/10.1007/978-3-319-06230-3
[13] Y. He, D.P. Nicholls and J. Shen, An efficient and stable spectral method for electromagnetic scattering from a layered periodic sructure, J. Comput. Phys. 231 (2012), pp. 3007–3022, https://doi.org/10.1016/j.jcp.2011.10.033
[14] C.O. Horgan, J.P. Spence, A. N. Andry, Lower bounds for eigenvalues of Sturm-Liouville problems with discontinuous coefficients: integral equation methods, Q. Appl. Math. 39 (1982), pp. 455–465, https://doi.org/10.1090/qam/644100
[15] Multi-precision Computing Toolbox for MATLAB. Yokohama: Advanpix LLC.; 2008-2017.
[16] M. Marletta, J.D. Pryce, Automatic solution of Sturm-Liouville problems using the Pruess method, J. Comput. Appl. Math. 39 (1992), pp. 57–78, https://doi.org/10.1016/0377-0427(92)90222-j
[17] O.S. Mukhtarov, M. Kadakal and F.S. Muhtarov, On discontinuous Sturm-Liouville problems with transmission conditions, J. Math. Kyoto Univ. (JMKYAZ) 44 (2004), pp. 779–798, https://doi.org/10.1215/kjm/1250281698
[18] J. Necas, Direct Methods in the Theory of Elliptic Equations, Springer Monographs in Mathematics. Berlin 2012, https://doi.org/10.1007/978-3-642-10455-8
[19] S. Pruess, C.T. Fulton, Mathematical Software for Sturm-Liouville Problems, ACM T. Math. Software. 19 (1993), pp. 360–376, https://doi.org/10.1145/155743.155791
[20] J. D. Pryce, Numerical solutions of Sturm-Liouville problem, Oxford University Press,Oxford, U. K., 1993.
[21] D.G. Shepelsky, The inverse problem of reconstruction of the medium’s conductivity in a class of discontinuous and increasing functions, Adv. Soviet Math. 19 (1994), pp.209–231.
[22] I. Titeux, Ya. Yakubov, Completeness of root functions for thermal conduction in a strip with piecewise continuous coefficients Math. Models Methods Appl. Sc., 7 (1997), pp. 1035–1050, https://doi.org/10.1142/S0218202597000529
[23] J.A.C. Weideman, S. C. Reddy, A MATLAB Differentiation Matrix Suite, ACM T. Math. Software. 26 (2000), pp. 465–519,
[24] A. Zettl, Adjoint and Self-Adjoint Boundary Value Problems with Interface Conditions,SIAM J. Appl. Math. 16 (1968), pp. 851–859.
[25] A. Zettl, Sturm—Liouville Theory, Math. Surveys Monogr., vol. 121, Amer. Math. Soc., Providence, RI 2005.
[26] H. Yserentant, A Short Theory of the Rayleigh-Ritz Method, C.M.A.M. 13 (2013) pp. 496–502, https://doi.org/10.1515/cmam-2013-0013
