Costica Mustata
“Tiberiu Popoviciu” Institute of Numerical Analysis, Romanian Academy, Romania
Keywords
Paper coordinates
C. Mustăţa, About the determination of extremes of Hölder functions, Seminar of Functional Analysis and Numerical Methods, Preprint Nr. 1 (1983), 107-116.
[1] G. Aronsson, Extension of functions satisfying Lipschitz conditions, Arkiv for Mathematik 6, 28 (1967), 551-561.
[2] J. Czipser and L. Geher, Extension of functions satisfying a Lipschitz condition, Acta Math. Acad. Sci. Hungar 6 (1955), 213-220.
[3] R. Levi and M.D., Rice, The Approximation of Uniformly Continuous Mappings by Lipschitz and Holder Mappings (prerint), 1980.
[4] E.J. McShane, Extension of range of functions, Bull. Amer. Math.Soc. 40 (1934), 837-842.
[5] C. Mustata, Best Approximation and Unique Extension of Lipschitz Functions, Journal Approx. Theory 19 (1977), 222-230.
[6] B. Shubert, A sequential method seeking the global maximum of a function, SIAM J. Numer. Anal. 9 (1972), 379-388.
[7] The Otto Dunkel Memorial Problem Book, New York (1957).
About the determination of extremes of Hölder functions
byCostica Mustata
Iot (X,d)(X,d)(X,d)(\mathrm{X}, \mathrm{d})(X,d) be a metric space and α∈(0,1]α∈(0,1]alpha in(0,1]\alpha \in(0,1]α∈(0,1]. A sunction δ:X→Bδ:X→Bdelta:XrarrB\delta: \mathrm{X} \rightarrow \mathrm{B}δ:X→B is called Hölder of eless ααalpha\alphaα on XXXXX if there exists K⩾0K⩾0K >= 0K \geqslant 0K⩾0 eveh that
(2)‖I‖α,x=sup{|f(x)−f(y)|/aα(x,y):x,y∈X,x∣y}(2)‖I‖α,x=sup|f(x)−f(y)|/aα(x,y):x,y∈X,x∣y{:(2)||I||_(alpha,x)=s u p{|f(x)-f(y)|//a^(alpha)(x,y):x,y in X,quad x∣y}:}\begin{equation*}
\|I\|_{\alpha, x}=\sup \left\{|f(x)-f(y)| / a^{\alpha}(x, y): x, y \in X, \quad x \mid y\right\} \tag{2}
\end{equation*}(2)‖I‖α,x=sup{|f(x)−f(y)|/aα(x,y):x,y∈X,x∣y}
Then ‖f‖α,X‖f‖α,X||f||_(alpha,X)\|f\|_{\alpha, X}‖f‖α,X is the smallest constant ZZZ\mathbb{Z}Z. for which the inequality (1) holds anditis called the Holder noxy of 1 .
Denote by Λα(x,d)Λα(x,d)Lambda_(alpha)(x,d)\Lambda_{\alpha}(x, d)Λα(x,d) the set of Hölder functions of class ααalpha\alphaα on XXXXX [3]. Then Λα(X,d)Λα(X,d)Lambda_(alpha)(X,d)\Lambda_{\alpha}(X, d)Λα(X,d) is a vector lattice, that is, it is closed under the operations of addition, multiplication by ecalars and formation of supremum and infimum of two of its elemonts.
For a nonvoid subset XXXXX of XXXXX, the Hölder norm. ‖f‖α,X‖f‖α,X||f||_(alpha,X)\|f\|_{\alpha, X}‖f‖α,X and the space Λα(Y,d)Λα(Y,d)Lambda_(alpha)(Y,d)\Lambda_{\alpha}(Y, d)Λα(Y,d) are defined similarly .
THEOREM 1. Ist (X,d)(X,d)(X,d)(X, d)(X,d) be a motric space, I⊂XI⊂XI sub XI \subset XI⊂X and α∈(0,1]α∈(0,1]alpha in(0,1]\alpha \in(0,1]α∈(0,1]. If I∈Λα(Y,d)I∈Λα(Y,d)I inLambda_(alpha)(Y,d)I \in \Lambda_{\alpha}(Y, d)I∈Λα(Y,d) then the functions
F1(x)=inf{f(y)+‖f‖α,y⋅dα(x,y):y∈Y},x∈YF1(x)=inff(y)+‖f‖α,y⋅dα(x,y):y∈Y,x∈YF_(1)(x)=i n f{f(y)+||f||_(alpha,y)*d^(alpha)(x,y):quad y in Y},quad x in YF_{1}(x)=\inf \left\{f(y)+\|f\|_{\alpha, y} \cdot d^{\alpha}(x, y): \quad y \in Y\right\}, \quad x \in YF1(x)=inf{f(y)+‖f‖α,y⋅dα(x,y):y∈Y},x∈Y
and
(3)I2(x)=sup{f(y)−‖f‖α,Y⋅dα˙(x,y):z,y∈Y},x∈X(3)I2(x)=supf(y)−‖f‖α,Y⋅dα˙(x,y):z,y∈Y,x∈X{:(3)I_(2)(x)=s u p{f(y)-||f||_(alpha,Y)*d^(alpha^(˙))(x,y):z,y in Y}","quad x in X:}\begin{equation*}
I_{2}(x)=\sup \left\{f(y)-\|f\|_{\alpha, Y} \cdot d^{\dot{\alpha}}(x, y): z, y \in Y\right\}, \quad x \in X \tag{3}
\end{equation*}(3)I2(x)=sup{f(y)−‖f‖α,Y⋅dα˙(x,y):z,y∈Y},x∈X
ax extensions of IIIII, 1.2.
a) F1|Y=F2|Y=1F1Y=F2Y=1F_(1)|Y=F_(2)|Y=1F_{1}\left|Y=F_{2}\right| Y=1F1|Y=F2|Y=1,
and
b) ‖F1‖α,X=‖F2‖α,X=‖x‖α,IF1α,X=F2α,X=‖x‖α,I||F_(1)||_(alpha,X)=||F_(2)||_(alpha,X)=||x||_(alpha,I)\left\|F_{1}\right\|_{\alpha, X}=\left\|F_{2}\right\|_{\alpha, X}=\|x\|_{\alpha, I}‖F1‖α,X=‖F2‖α,X=‖x‖α,I.
Theorem 1 follows from Corollary 1.2 in [3] (see also [1],[2]). Let (X,d)(X,d)(X,d)(X, d)(X,d) be a compact metric space and let IIIII be in Λα(X,d)Λα(X,d)Lambda_(alpha)(X,d)\Lambda_{\alpha}(X, d)Λα(X,d). If YYYYY is a subset of XXXXX and q>‖P|Y‖α,Yq>PYα,Yq > ||P|_(Y)||_(alpha,Y)q>\left\|\left.P\right|_{Y}\right\|_{\alpha, Y}q>‖P|Y‖α,Y (kere I|YIYI|_(Y)\left.I\right|_{Y}I|Y denotes the restriction of III\mathcal{I}I to YYYYY ), then the functions
U(x)=inf{f(y)+q⋅dα(x,y):y∈I},x∈XU(x)=inff(y)+q⋅dα(x,y):y∈I,x∈XU(x)=inf{f(y)+q*d^(alpha)(x,y):y in I},x in XU(x)=i n f\left\{f(y)+q \cdot d^{\alpha}(x, y): y \in I\right\}, x \in XU(x)=inf{f(y)+q⋅dα(x,y):y∈I},x∈X
and
(4)u(x)=sup{f(y)−q⋅dα(x,y):y∈Y},x∈X(4)u(x)=supf(y)−q⋅dα(x,y):y∈Y,x∈X{:(4)u(x)=s u p{f(y)-q*d^(alpha)(x,y):y in Y}","x in X:}\begin{equation*}
u(x)=\sup \left\{f(y)-q \cdot d^{\alpha}(x, y): y \in Y\right\}, x \in X \tag{4}
\end{equation*}(4)u(x)=sup{f(y)−q⋅dα(x,y):y∈Y},x∈X
(8)Mf=sup{f(x):x∈X}.Bf={x∈X:P(x)=Mf}(8)Mf=sup{f(x):x∈X}.Bf=x∈X:P(x)=Mf{:(8)M_(f)=s u p{f(x):x in X}.quadB_(f)={x in X:P(x)=M_(f)}:}\begin{equation*}
M_{f}=\sup \{f(x): x \in X\} . \quad B_{f}=\left\{x \in X: P(x)=M_{f}\right\} \tag{8}
\end{equation*}(8)Mf=sup{f(x):x∈X}.Bf={x∈X:P(x)=Mf}
and for q>‖f|Y‖α,Xq>fYα,Xq > ||f|_(Y)||_(alpha,X)q>\left\|\left.f\right|_{Y}\right\|_{\alpha, X}q>‖f|Y‖α,X we have
A meximum (respectively a minimum) point of a function fi X→RX→RX rarr RX \rightarrow RX→R is a point X∗∈XX∗∈XX^(**)in XX^{*} \in XX∗∈X such that
for all x∈Xx∈Xx inXx \in \mathbb{X}x∈X.
For a bounded real function fffff on XXXXX put
are extensions of f|YfYf|_(Y)\left.f\right|_{Y}f|Y which belong to Λα(X,d)Λα(X,d)Lambda_(alpha)(X,d)\Lambda_{\alpha}(X, d)Λα(X,d) and have the norms qqqqq (see [2]). If F1F1F_(1)F_{1}F1 and F2F2F_(2)F_{2}F2 denotes the functions defined by (3), then
(5)F2(x)⩽f(x)⩽F1(x),x∈X(5)F2(x)⩽f(x)⩽F1(x),x∈X{:(5)F_(2)(x) <= f(x) <= F_(1)(x)","quad x in X:}\begin{equation*}
F_{2}(x) \leqslant f(x) \leqslant F_{1}(x), \quad x \in X \tag{5}
\end{equation*}(5)F2(x)⩽f(x)⩽F1(x),x∈X
and for q>‖f|Y‖α,Xq>fYα,Xq > ||f|_(Y)||_(alpha,X)q>\left\|\left.f\right|_{Y}\right\|_{\alpha, X}q>‖f|Y‖α,X we have
(6)u(x)⩽P2(x)⩽I(x)⩽P1(x)⩽U(x),x∈X(6)u(x)⩽P2(x)⩽I(x)⩽P1(x)⩽U(x),x∈X{:(6)u(x) <= P_(2)(x) <= I(x) <= P_(1)(x) <= U(x)","quad x in X:}\begin{equation*}
u(x) \leqslant P_{2}(x) \leqslant I(x) \leqslant P_{1}(x) \leqslant U(x), \quad x \in X \tag{6}
\end{equation*}(6)u(x)⩽P2(x)⩽I(x)⩽P1(x)⩽U(x),x∈X
A maximum (respectively a minimum) point of a function
if X→RX→RX rarr RX \rightarrow RX→R is a point x∗∈Xx∗∈Xx^(**)in Xx^{*} \in Xx∗∈X such that x∈Xx∈Xx in Xx \in Xx∈X.
∴∴:.\therefore∴
(9)ηf=Lnf{f(x):x∈I},ef={x∈I,f(x)=af}(9)ηf=Lnf{f(x):x∈I},ef=x∈I,f(x)=af{:(9)eta_(f)=Lnf{f(x):x in I}","quade_(f)={x in I,f(x)=a_(f)}:}\begin{equation*}
\eta_{f}=\operatorname{Lnf}\{f(x): x \in I\}, \quad e_{f}=\left\{x \in I, f(x)=a_{f}\right\} \tag{9}
\end{equation*}(9)ηf=Lnf{f(x):x∈I},ef={x∈I,f(x)=af}
Iot now ( X,dX,dX,dX, dX,d ) be a compact metric space and lot fffff be a function in Λα(X0,d)ΛαX0,dLambda_(alpha)(X_(0),d)\Lambda_{\alpha}\left(X_{0}, d\right)Λα(X0,d).
We define now inductively two sequences (zn)n≥0znn≥0(z_(n))_(n >= 0)\left(z_{n}\right)_{n \geq 0}(zn)n≥0 and (Mn)n≥0Mnn≥0(M_(n))_(n >= 0)\left(M_{n}\right)_{n \geq 0}(Mn)n≥0 of points in XXXXX and of real numbers, respectively, as follows :
Ift Q>‖&‖α,IQ>‖&‖α,IQ > ||&||_(alpha,I)Q>\|\&\|_{\alpha, I}Q>‖&‖α,I be fired and lot x0x0x_(0)x_{0}x0 be a fixed point in xxxxx. Let
(20)v0(x)=P(x0)+q⋅dα(x0x0),z∈X(20)v0(x)=Px0+q⋅dαx0x0,z∈X{:(20)v^(0)(x)=P(x_(0))+q*d^(alpha)(x_(0)x_(0))quad","quad z in X:}\begin{equation*}
v^{0}(x)=P\left(x_{0}\right)+q \cdot d^{\alpha}\left(x_{0} x_{0}\right) \quad, \quad z \in X \tag{20}
\end{equation*}(20)v0(x)=P(x0)+q⋅dα(x0x0),z∈X
the greatest extension of fffff obtained from (4) for I I = {x0}x0{x_(0)}\left\{x_{0}\right\}{x0} and 10t
M0=sup{π0(x),x∈X}.M0=supπ0(x),x∈X.M_(0)=s u p{pi^(0)(x),x in X}.M_{0}=\sup \left\{\pi^{0}(x), x \in X\right\} .M0=sup{π0(x),x∈X}.
Suppose now that for a natural number n⩾1n⩾1n >= 1n \geqslant 1n⩾1, the points z0,x1,…,zn−1z0,x1,…,zn−1z_(0),x_(1),dots,z_(n-1)z_{0}, x_{1}, \ldots, z_{n-1}z0,x1,…,zn−1 and the number M0,M1,…,Mn−1M0,M1,…,Mn−1M_(0),M_(1),dots,M_(n-1)M_{0}, M_{1}, \ldots, M_{n-1}M0,M1,…,Mn−1 were defined. Let σn−1σn−1sigma^(n-1)\sigma^{n-1}σn−1 be the greatest extension of I|YIYI|_(Y)\left.\mathcal{I}\right|_{Y}I|Y obtained from (4) for Y={x0,x1,…,xn−1}Y=x0,x1,…,xn−1Y={x_(0),x_(1),dots,x_(n-1)}Y=\left\{x_{0}, x_{1}, \ldots, x_{n-1}\right\}Y={x0,x1,…,xn−1}. Put yn=sup{0n−1(x)yn=sup0n−1(x)y_(n)=s u p{0^(n-1)(x):}y_{n}=\sup \left\{0^{n-1}(x)\right.yn=sup{0n−1(x); 0x∈X}0x∈X}0x in X}0 x \in X\}0x∈X} and lot xnxnx_(n)x_{n}xn be a point in XXXXX such that Un−1(za)=ξaUn−1za=ξaU^(n-1)(z_(a))=xi_(a)U^{n-1}\left(z_{a}\right)=\xi_{a}Un−1(za)=ξa.
The properties of the so defined sequences (xa)a≥0xaa≥0(x_(a))_(a >= 0)\left(x_{a}\right)_{a \geq 0}(xa)a≥0 and. (ya)n⩾0yan⩾0(y_(a))_(n >= 0)\left(y_{a}\right)_{n \geqslant 0}(ya)n⩾0 are described in the following theorem:
TH80REM 2. Let ( I,dI,dI,dI, dI,d ) be a compact metric space and let f∈Λα(x,d)f∈Λα(x,d)f inLambda_(alpha)(x,d)f \in \Lambda_{\alpha}(x, d)f∈Λα(x,d). For a fired q>‖f‖α,xq>‖f‖α,xq > ||f||_(alpha,x)q>\|f\|_{\alpha, x}q>‖f‖α,x let the sequences (xΔ)n=0xΔn=0(x_(Delta))_(n=0)\left(x_{\Delta}\right)_{n=0}(xΔ)n=0 and (Ma)n>0Man>0(M_(a))_(n > 0)\left(M_{a}\right)_{n>0}(Ma)n>0 be defined as above. Then
a) lima→∞Ma=Mblima→∞Ma=Mblim_(a rarr oo)M_(a)=M_(b)\lim _{a \rightarrow \infty} M_{a}=M_{b}lima→∞Ma=Mb :
b) limn→∞limn→∞lim_(n rarr oo)\lim _{n \rightarrow \infty}limn→∞ inf {a(x,xn),x∈Ef}=0ax,xn,x∈Ef=0{a(x,x_(n)),x inE_(f)}=0\left\{a\left(x, x_{n}\right), x \in \mathbb{E}_{f}\right\}=0{a(x,xn),x∈Ef}=0;
0)The sequence (I(za))a⩾0Izaa⩾0(I(z_(a)))_(a >= 0)\left(I\left(z_{a}\right)\right)_{a \geqslant 0}(I(za))a⩾0 has the number If ase as
Zinit point-
Proof.Since πn⩽πn−1πn⩽πn−1pi^(n) <= pi^(n-1)\pi^{n} \leqslant \pi^{n-1}πn⩽πn−1 for B=1,2,…B=1,2,…B=1,2,dotsB=1,2, \ldotsB=1,2,… ,it rollows that the sequence ( 第 )a⩾0( 第 )a⩾0(" 第 ")_(a >= 0)(\text { 第 })_{a \geqslant 0}第( 第 )a⩾0 is nondecreasing .By(6)ya=vn−1(xa)⩾⩾f(xa)⩾min{f(x)ya=vn−1xa⩾⩾fxa⩾min{f(x)y_(a)=v^(n-1)(x_(a))⩾⩾f(x_(a)) >= min{f(x)y_{a}=v^{n-1}\left(x_{a}\right) \geqslant \geqslant f\left(x_{a}\right) \geqslant \min \{f(x)ya=vn−1(xa)⩾⩾f(xa)⩾min{f(x) s x∈I}x∈I}x in I}x \in I\}x∈I} so that the sequence (ha)m⩾018sham⩾018s(h_(a))_(m >= 0)(18 )/(s)\left(h_{a}\right)_{m \geqslant 0} \frac{18}{s}(ha)m⩾018s also bounded .Therefore there exiets M=1±3IgM=1±3IgM=1+-3IgM=1 \pm 3 \mathrm{Ig}M=1±3Ig .By(6) f(x)≤fn(x)≤I,f(x)≤fn(x)≤I,f(x) <= f^(n)(x) <= I,quadf(x) \leq f^{n}(x) \leq I, \quadf(x)≤fn(x)≤I, for all x∈Xx∈Xx in Xx \in Xx∈X and a∈Ia∈Ia in Ia \in Ia∈I so that
(21)f(x)⩽ 贴, for all x∈x(21)f(x)⩽ 贴, for all x∈x{:(21)f(x) <= " 贴, for all "x in x:}\begin{equation*}
f(x) \leqslant \text { 贴, for all } x \in x \tag{21}
\end{equation*}贴(21)f(x)⩽ 贴, for all x∈x
The metric space zzzzz being compact,the sequence (zn)n≥0znn≥0(z_(n))_(n >= 0)\left(z_{n}\right)_{n \geq 0}(zn)n≥0 contains a subsequence (znk)k⩾0znkk⩾0(z_(n_(k)))_(k >= 0)\left(z_{n_{k}}\right)_{k \geqslant 0}(znk)k⩾0 convergent to a point z∈Xz∈Xz in Xz \in Xz∈X . Since the function if is continuous it follows that
(12)f(xnk)→f(z1),k→∞(12)fxnk→fz1,k→∞{:(12)f(x_(n_(k)))rarr f(z_(1))quad","quad k rarr oo:}\begin{equation*}
f\left(x_{n_{k}}\right) \rightarrow f\left(z_{1}\right) \quad, \quad k \rightarrow \infty \tag{12}
\end{equation*}(12)f(xnk)→f(z1),k→∞
But,for k⩾1k⩾1k >= 1k \geqslant 1k⩾1 , |vnk−1(z)−nnk−1|=|vnk−1(z)−vnk−1(znk)|≤q⋅dα(zvznk)→0vnk−1(z)−nnk−1=vnk−1(z)−vnk−1znk≤q⋅dαzvznk→0|v^(n_(k)-1)(z)-n_(n_(k)-1)|=|v^(n_(k)-1)(z)-v^(n_(k)-1)(z_(n_(k)))| <= q*d^(alpha)(z_(v)z_(n_(k)))rarr0\left|v^{n_{k}-1}(z)-n_{n_{k}-1}\right|=\left|v^{n_{k}-1}(z)-v^{n_{k}-1}\left(z_{n_{k}}\right)\right| \leq q \cdot d^{\alpha}\left(z_{v} z_{n_{k}}\right) \rightarrow 0|vnk−1(z)−nnk−1|=|vnk−1(z)−vnk−1(znk)|≤q⋅dα(zvznk)→0
for k→∞k→∞k rarr ook \rightarrow \inftyk→∞ ,and Mk−1→MMk−1→MM_(k^(-1))rarr MM_{k^{-1}} \rightarrow MMk−1→M for k→∞k→∞k rarr ook \rightarrow \inftyk→∞ ,so that
(13)vnk−1(z)→I, for k→∞(13)vnk−1(z)→I, for k→∞{:(13)v^(n_(k)-1)(z)rarrIquad","" for "krarr oo:}\begin{equation*}
\mathrm{v}^{\mathrm{n}_{k}-1}(\mathrm{z}) \rightarrow \mathrm{I} \quad, \text { for } \mathrm{k} \rightarrow \infty \tag{13}
\end{equation*}(13)vnk−1(z)→I, for k→∞
By the relation |∇nk(z)−f(znk)|=|∇nk(z)−vnk(znk)|≤q⋅dα(z,xnk)→0,k→∞∇nk(z)−fznk=∇nk(z)−vnkznk≤q⋅dαz,xnk→0,k→∞|grad^(n_(k))(z)-f(z_(n_(k)))|=|grad^(n_(k))(z)-v^(n_(k))(z_(n_(k)))| <= q*d^(alpha)(z,x_(n_(k)))rarr0,k rarr oo\left|\nabla^{n_{k}}(z)-f\left(z_{n_{k}}\right)\right|=\left|\nabla^{n_{k}}(z)-v^{n_{k}}\left(z_{n_{k}}\right)\right| \leq q \cdot d^{\alpha}\left(z, x_{n_{k}}\right) \rightarrow 0, k \rightarrow \infty|∇nk(z)−f(znk)|=|∇nk(z)−vnk(znk)|≤q⋅dα(z,xnk)→0,k→∞, and by(12)it follows that
we lot k→∞k→∞k rarr ook \rightarrow \inftyk→∞ one obtains l(g)≤l≤l(g)l(g)≤l≤l(g)l(g) <= l <= l(g)l(g) \leq l \leq l(g)l(g)≤l≤l(g) ,so that f(z)=Mf(z)=Mf(z)=Mf(z)=Mf(z)=M . Taking into account(11)it follows that
for all j∈Jj∈Jj in Jj \in Jj∈J .The space XXXXX being compact there exists a subse- quence (xjk)k⩾0xjkk⩾0(x_(j_(k)))_(k >= 0)\left(x_{j_{k}}\right)_{k \geqslant 0}(xjk)k⩾0 of (xj)j∈Jxjj∈J(x_(j))_(j in J)\left(x_{j}\right)_{j \in J}(xj)j∈J converging to a point y∈Xy∈Xy in Xy \in Xy∈X .But then,ropeating the above arguments will follow that y∈Kfy∈Kfy inK_(f)y \in K_{f}y∈Kf , which contradicts(15).
The affination c)follows from(12).
Remarks.1)In the case X≈[a,b]X≈[a,b]X~~[a,b]X \approx[a, b]X≈[a,b] and α=1α=1alpha=1\alpha=1α=1 a similar result in proved in[6].
2)If the extensions vnvnv^(n)v^{n}vn are replaced by the extensions ununu^(n)u^{n}un and gΩ=inf{aiA(x)ix∈X},unA(xa+j)=magΩ=infaiA(x)ix∈X,unAxa+j=mag_(Omega)=i n f{a^(i_(A))(x)quad i quad x in X},u^(n^(A))(x_(a+j))=m_(a)g_{\Omega}=\inf \left\{a^{i_{A}}(x) \quad i \quad x \in X\right\}, u^{n^{A}}\left(x_{a+j}\right)=m_{a}gΩ=inf{aiA(x)ix∈X},unA(xa+j)=ma ,then one obtains a procedure to find the minimum.gfgfg_(f)g_{f}gf of a function f∈Λα(X,df∈Λα(X,df inLambda_(alpha)(X,df \in \Lambda_{\alpha}(X, df∈Λα(X,d
Exaaple.Let X=[0,1],d(x,y)=|x−y|X=[0,1],d(x,y)=|x−y|X=[0,1],d(x,y)=|x-y|X=[0,1], d(x, y)=|x-y|X=[0,1],d(x,y)=|x−y| and
f(x)=x⋅sinix, if x∈(0,1]=0, if x=0f(x)=x⋅sinix, if x∈(0,1]=0, if x=0{:[f(x)=x*sin((i)/(x))","," if "x in(0","1]],[=0,","" if "x=0]:}\begin{array}{cl}
f(x)=x \cdot \sin \frac{i}{x}, & \text { if } x \in(0,1] \\
=0 & , \text { if } x=0
\end{array}f(x)=x⋅sinix, if x∈(0,1]=0, if x=0
It is known that f∈Λα(α,d)f∈Λα(α,d)f inLambda_(alpha)(alpha,d)f \in \Lambda_{\alpha}(\alpha, d)f∈Λα(α,d) if and only if α∈(0,12]α∈0,12alpha in(0,(1)/(2)]\alpha \in\left(0, \frac{1}{2}\right]α∈(0,12] (see [7], Probiem 153) and in this caee
We apply now Theorem 2 to find the global maximum of the function fffff on [0,1/π][0,1/π][0,1//pi][0,1 / \pi][0,1/π] for α=1/2α=1/2alpha=1//2\alpha=1 / 2α=1/2.
Step 0. Take x0=1/2πx0=1/2πx_(0)=1//2pi\mathrm{x}_{0}=1 / 2 \pix0=1/2π.
The greatest extension of f|{x0}fx0f|_({x_(0)})\left.f\right|_{\left\{x_{0}\right\}}f|{x0} to [0,1/π][0,1/π][0,1//pi][0,1 / \pi][0,1/π] is U0(x)=f(x0)+4|x−x0|1/2U0(x)=fx0+4x−x01/2U^(0)(x)=f(x_(0))+4|x-x_(0)|^(1//2)U^{0}(x)=f\left(x_{0}\right)+4\left|x-x_{0}\right|^{1 / 2}U0(x)=f(x0)+4|x−x0|1/2
The set of points of local maximum of the function U0U0U^(0)U^{0}U0 is D0={(0,4/2π),(2/π,4/2π)}D0={(0,4/2π),(2/π,4/2π)}D_(0)={(0,4//sqrt(2pi)),(2//pi,4//sqrt(2pi))}D_{0}=\{(0,4 / \sqrt{2 \pi}),(2 / \pi, 4 / \sqrt{2 \pi})\}D0={(0,4/2π),(2/π,4/2π)}.
Step 1. Take x1=1/πx1=1/πx_(1)=1//pix_{1}=1 / \pix1=1/π, and let U1U1U^(1)U^{1}U1 be the greatest extension of f∣{x0,x1}f∣x0,x1f∣{x_(0),x_(1)}f \mid\left\{x_{0}, x_{1}\right\}f∣{x0,x1} io [0,1/π][0,1/π][0,1//pi][0,1 / \pi][0,1/π], that is U1(x)=min{f(xk)+4|x−xk|1/2k,k∈{0,1}}U1(x)=minfxk+4x−xk1/2k,k∈{0,1}U^(1)(x)=min{f(x_(k))+4|x-x_(k)|^(1//2)quad k,k in{0,1}}U^{1}(x)=\min \left\{f\left(x_{k}\right)+4\left|x-x_{k}\right|^{1 / 2} \quad k, k \in\{0,1\}\right\}U1(x)=min{f(xk)+4|x−xk|1/2k,k∈{0,1}}
The points of local maximum of the function 02020^(2)0^{2}02 is D1={(xo1,U1(xo1)),(0,U1(0))}D1=xo1,U1xo1,0,U1(0)D_(1)={(x_(o1),U^(1)(x_(o1))),(0,U^(1)(0))}D_{1}=\left\{\left(x_{o 1}, U^{1}\left(x_{o 1}\right)\right),\left(0, U^{1}(0)\right)\right\}D1={(xo1,U1(xo1)),(0,U1(0))}
Where xo1xo1x_(o1)x_{o 1}xo1 is the solution of the equation
belonging to [x0;x1]x0;x1[x_(0);x_(1)]\left[x_{0} ; x_{1}\right][x0;x1] and let x2=0x2=0x_(2)=0x_{2}=0x2=0.
Step 2. Let π2π2pi^(2)\pi^{2}π2 be the greatest extension of l′∣{x0,x1,x2}l′∣x0,x1,x2l^(')∣{x_(0),x_(1),x_(2)}l^{\prime} \mid\left\{x_{0}, x_{1}, x_{2}\right\}l′∣{x0,x1,x2} to [0,2/π][0,2/π][0,2//pi][0,2 / \pi][0,2/π]. Let D2={(x12,π2(x12)),(x01,π2(x01))}D2=x12,π2x12,x01,π2x01D_(2)={(x_(12),pi^(2)(x_(12))),(x_(01),pi^(2)(x_(01)))}D_{2}=\left\{\left(x_{12}, \pi^{2}\left(x_{12}\right)\right),\left(x_{01}, \pi^{2}\left(x_{01}\right)\right)\right\}D2={(x12,π2(x12)),(x01,π2(x01))}
be the set of points of local maximum of the function σ2σ2sigma^(2)\sigma^{2}σ2 and let x3=x01x3=x01x_(3)=x_(01)x_{3}=x_{01}x3=x01.
Step a . Let UnUnU^(n)\mathrm{U}^{\mathrm{n}}Un be the greatest extension of the function f∣{x0,x1,…,xn}f∣x0,x1,…,xnf∣{x_(0),x_(1),dots,x_(n)}f \mid\left\{x_{0}, x_{1}, \ldots, x_{n}\right\}f∣{x0,x1,…,xn} to [0,1/π][0,1/π][0,1//pi][0,1 / \pi][0,1/π] and let xn+1xn+1x_(n+1)x_{n+1}xn+1 be the greatest of the abscisses of the poits of the global 昷aximum of UnUnU^(n)U^{n}Un.
To stop the algorithm one can proceeds in two ways :
a) the algorithm stops after a fixed number of iterations &
b) the algorithm stops when the difference between the global maximum Un(xM)UnxMU^(n)(x_(M))U^{n}\left(x_{M}\right)Un(xM) of the function UnUnU^(n)U^{n}Un and f(xM)fxMf(x_(M))f\left(x_{M}\right)f(xM) is smaller than a fixed number ε>0ε>0epsi > 0\varepsilon>0ε>0.
We have programmed this algorithm in the language BASIC with n=300n=300n=300n=300n=300 iterations.
The program is the following . 8
1 OPEN'LP: 'FOROUTPUT ASFILEITO WRITW
10 INPUT X%=X%+18Y%=2∗Z%X%=X%+18Y%=2∗Z%X%=X%+18Y%=2^(**)Z%\mathrm{X} \%=\mathrm{X} \%+18 \mathrm{Y} \%=2{ }^{*} \mathrm{Z} \%X%=X%+18Y%=2∗Z% 20DIMX(Y%),F1(X%),FZ(X%)20DIMX(Y%),F1(X%),FZ(X%)20DIMX(Y%),F1(X%),FZ(X%)20 \mathrm{DIM} \mathrm{X}(\mathrm{Y} \%), \mathrm{F} 1(\mathrm{X} \%), \mathrm{FZ}(\mathrm{X} \%)20DIMX(Y%),F1(X%),FZ(X%) 25M=1;P%=025M=1;P%=025M=1;P%=025 \mathrm{M}=1 ; \mathrm{P} \%=025M=1;P%=0
30 DEF FN F(X)F(X)F(X)F(X)F(X)
31 IF X=0X=0X=0X=0X=0 THEN FNF =0=0=0=0=0 ELSE 33
32 GO TO 35 33FNE=X∗SIN(1./X)33FNE=X∗SIN(1./X)33FNE=X^(**)SIN(1.//X)33 \mathrm{FNE}=\mathrm{X}^{*} \mathrm{SIN}(1 . / \mathrm{X})33FNE=X∗SIN(1./X)
35 FNEND
40 DEF FN P(X,U)=FNP(U)+3.355∗SQR(ABS(X!U))P(X,U)=FNP(U)+3.355∗SQR(ABS(X!U))P(X,U)=FNP(U)+3.355^(**)SQR(ABS(X!U))P(X, U)=F N P(U)+3.355^{*} \operatorname{SQR}(A B S(X!U))P(X,U)=FNP(U)+3.355∗SQR(ABS(X!U))
II 82>=X282>=X282>=X282>=X 282>=X2 Am 81<=Y81<=Y81<=Y81<=Y81<=Y GO 20110
100
82=1−B282=1−B282=1-B282=1-B 282=1−B2
110
FITB =81=81=81=81=81
120
FINETD
130
X(1)=0&X(2)=1./PI&X(3)=1./(2.∗PI)X(1)=0&X(2)=1./PI&X(3)=1./2.∗PIX(1)=0&X(2)=1.//PI&X(3)=1.//(2.^(**)PI)X(1)=0 \& X(2)=1 . / P I \& X(3)=1 . /\left(2 .{ }^{*} P I\right)X(1)=0&X(2)=1./PI&X(3)=1./(2.∗PI)
50 DEF WH B(X,Y)
60 A=I+X
70 D=(HEP(Y)-HSE(X))//3.3558 D=D^(**)D \&富=X-X
75 D3 =D^(**)(E+E-D)
80 BI=(A+SQR(D3))/2.
90 II 82>=X2 Am 81<=Y GO 20110
100 82=1-B2
110 FITB =81
120 FINETD
130 X(1)=0&X(2)=1.//PI&X(3)=1.//(2.^(**)PI)
140 I\%~~3:J%=1:P2(J%)=MP(X(1),X(3)),M1(J%)~~X(1)
150 J%=J%+1:E2(J%)=MPP(X(2),X(3)),FI(J%)=X(2)
160 Sigmasigma_(日)=188=>F2(1)
3.70 BOR E\%=2 20J%
180 https://cdn.mathpix.com/cropped/2025_09_08_ff27670f11cd2d1aba5ag-5.jpg?height=64&width=815&top_left_y=996&top_left_x=361
190 MEXYS K\%
200 D1=X(1)-X(2) \&V1%=0 ;V2%=0 :D2=-D1,CaI1(If)
210 FOR K%=1 TO \%
220 Tax(K\%)-0
230 IF T<0 THEST 240 ETBE 250
240 If T < D1 THEN ; 250 ET8S D1=T_(1) : 71%= K
250 II (m)/(2) > 0 सादता 2010 STSE 1020
1010 IF T D2 THEN 1020 ELSE D2=T \&V2\%-K\%
1020 NEXT K\%
1030 IF V1\%=0 THEN 1070
1040 姐 =I%:I%=I%+1
1050 X(I%)=MNS(X(V1%),0)| 50 DEF WH B(X,Y) | |
| :--- | :--- |
| 60 | $\mathrm{A}=\mathrm{I}+\mathrm{X}$ |
| 70 | $D=(\operatorname{HEP}(Y)-\operatorname{HSE}(X)) / 3.3558 D=D^{*} D$ \&富=X-X |
| 75 | D3 $=D^{*}(E+E-D)$ |
| 80 | BI=(A+SQR(D3))/2. |
| 90 | II $82>=X 2$ Am $81<=Y$ GO 20110 |
| 100 | $82=1-B 2$ |
| 110 | FITB $=81$ |
| 120 | FINETD |
| 130 | $X(1)=0 \& X(2)=1 . / P I \& X(3)=1 . /\left(2 .{ }^{*} P I\right)$ |
| 140 | I\%$\approx 3: J \%=1: P 2(J \%)=\operatorname{MP}(X(1), X(3)), \operatorname{M1(J\% )} \approx X(1)$ |
| 150 | $J \%=J \%+1: \operatorname{E2}(J \%)=\operatorname{MPP}(X(2), X(3)), \operatorname{FI}(J \%)=X(2)$ |
| 160 | $\Sigma \sigma_{日}=188 \Rightarrow \mathrm{~F} 2(1)$ |
| 3.70 | BOR E\%=2 $20 \mathrm{~J} \mathrm{\%}$ |
| 180 | 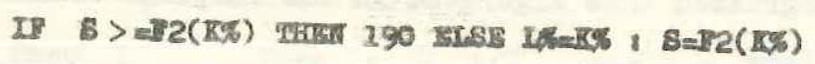 |
| 190 | MEXYS K\% |
| 200 | $D 1=X(1)-X(2)$ \&$V 1 \%=0$ ;$V 2 \%=0$ :D2=-D1,CaI1(If) |
| 210 | FOR $K \%=1$ TO \% |
| 220 | Tax(K\%)-0 |
| 230 | IF T<0 THEST 240 ETBE 250 |
| 240 | If $\mathrm{T}<\mathrm{D} 1$ THEN ; 250 ET8S $\mathrm{D} 1=\mathrm{T}_{1}$ : $71 \%=$ K |
| 250 | II $\frac{m}{2}>0$ सादता 2010 STSE 1020 |
| 1010 | IF T D2 THEN 1020 ELSE D2=T \&V2\%-K\% |
| 1020 | NEXT K\% |
| 1030 | IF V1\%=0 THEN 1070 |
| 1040 | 姐 $=I \%: I \%=I \%+1$ |
| 1050 | $\mathrm{X}(\mathrm{I} \%)=\operatorname{MNS}(\mathrm{X}(\mathrm{V} 1 \%), 0)$ |
1070 II V2\%कासारा 1140
1080 正自3\%←1←1larr1\leftarrow 1←1 1090X(I%)=MB(C,X(V2%))1090X(I%)=MB(C,X(V2%))1090 X(I%)=MB(C,X(V2%))1090 X(I \%)=M B(C, X(V 2 \%))1090X(I%)=MB(C,X(V2%))
3100 IT V1\%=0 THEN 2110 ELEES 1120
1120 J %=3%+1%=3%+1%=3%+1\%=3 \%+1%=3%+1
1125 제 ग\%-8\%-1 O2 I\%I F⿻丷木-1 स्पष्म 2150 D Y.MYTENUEISE1135:P\%=7%=7%=7%=7 \%=7%
1135 ए J%=X%J%=X%J%=X%J \%=X \%J%=X% OR I%=X%I%=X%I%=X%I \%=X \%I%=X% शन्सरण 1150
1140 II ABS(ABS(ABS(\operatorname{ABS}(ABS( F2(J\%)-FNE (X(I%)))<1.E−3(X(I%)))<1.E−3(X(I%))) < 1.E-3(\mathrm{X}(\mathrm{I} \%)))<1 . \mathrm{E}-3(X(I%)))<1.E−3 THEN 1150 ETSZ 160
1151 PRI \#1,\&PRI \&1,"B-AU YACUT"B J\%"JIERATII" 1155PRI≠1,8PRI⇒1,∘X′&TAB(11);′F(X)′&TAB(21);∘P(X)′&TAB(33)g′X′&&TAB(43);′P(x)′1155PRI≠1,8PRI⇒1,∘X′&TAB(11);′F(X)′&TAB(21);∘P(X)′&TAB(33)g′X′&&TAB(43);′P(x)′1155 PRI!=1,8PRI=>1,^(@)X^(')&TAB(11);^(')F(X)^(')&TAB(21);^(@)P(X)^(')&TAB(33)g^(')X^(')&quad&TAB(43);^(')P(x)^(')1155 P R I \neq 1,8 P R I \Rightarrow 1,{ }^{\circ} X^{\prime} \& T A B(11) ;{ }^{\prime} F(X)^{\prime} \& T A B(21) ;{ }^{\circ} P(X)^{\prime} \& T A B(33) g^{\prime} X^{\prime} \& \quad \& \operatorname{TAB}(43) ;{ }^{\prime} P(x)^{\prime}1155PRI≠1,8PRI⇒1,∘X′&TAB(11);′F(X)′&TAB(21);∘P(X)′&TAB(33)g′X′&&TAB(43);′P(x)′ \& 2 AB (53);′P(x)′(53);′P(x)′(53);^(')P(x)^(')(53) ;{ }^{\prime} P(x)^{\prime}(53);′P(x)′ ; TAB(207);′F(X)′′F(X)′^(')F(X)^('){ }^{\prime} F(X)^{\prime}′F(X)′ ;TAB(117);′P(X)′′P(X)′^(')P(X)^('){ }^{\prime} P(X)^{\prime}′P(X)′ \&PRI \#I。 I。 I_("。 ")I_{\text {。 }}。I。 FIX(II(K\%));E2(K\%);FOR K\%=1 TO J\%-1
1180 PRI \#1,8 PRI \#1,8 PRI \#1,∘∘^(@){ }^{\circ}∘ SOL APROXINATIVA ′′′X=′gF1(P%)′′′X=′gF1(P%)^(')^(')^(')X=^(')gF1(P%){ }^{\prime}{ }^{\prime}{ }^{\prime} \mathrm{X}={ }^{\prime} \mathrm{g} F 1(\mathrm{P} \%)′′′X=′gF1(P%) ;\& ′F(X)=′;FNP(FI(P%);′P(X)=′ξF2(P%)′F(X)=′;FNPFI(P%);′P(X)=′ξF2(P%)^(')F(X)=^(');FNP(FI(P%);^(')P(X)=^(')xi F2(P%):}{ }^{\prime} F(X)={ }^{\prime} ; F N P\left(F I(P \%) ;^{\prime} P(X)={ }^{\prime} \xi F 2(P \%)\right.′F(X)=′;FNP(FI(P%);′P(X)=′ξF2(P%) ;'DELMA='\&\& ABS(B2(P\%)-FNF(FI(P\%))) 11840=1./7111840=1./7111840=1.//7111840=1 . / 7111840=1./71(P\%)
1185PRT \#1, 2 PRI \#1,"VATOARRA DERIVATTEL :I′(X¯)=#%I′(X¯)=#%I^(')( bar(X))=^(#)%I^{\prime}(\bar{X})={ }^{\#} \%I′(X¯)=#% SIW (U¯)−U∗cOS(U)(U¯)−U∗cOS(U)( bar(U))-U^(**)cOS(U)(\bar{U})-U^{*} \operatorname{cOS}(U)(U¯)−U∗cOS(U) 1190 푼()
One can show that in this case the sequence (xa)ajexaaje(x_(a))_(aje)\left(x_{a}\right)_{a j e}(xa)aje conver- ges to the maximum point z∗=0.12944z∗=0.12944z^(**)=0.12944z^{*}=0.12944z∗=0.12944(the solution of the equate tion tg(1/x)=1/x,x∈(1/3π,1/2π))tg(1/x)=1/x,x∈(1/3π,1/2π))tg(1//x)=1//x,x in(1//3pi,1//2pi))\operatorname{tg}(1 / x)=1 / x, x \in(1 / 3 \pi, 1 / 2 \pi))tg(1/x)=1/x,x∈(1/3π,1/2π)) .
The maximum of fffff is ξf=2(x∗)=0.128374ξf=2x∗=0.128374xi_(f)=2(x^(**))=0.128374\xi_{f}=2\left(x^{*}\right)=0.128374ξf=2(x∗)=0.128374 .Arter 300 ite- ration we have obtained the following results \& x300=0.129982x300=0.129982x_(300)=0.129982x_{300}=0.129982x300=0.129982 f(x300)=0.128309fx300=0.128309f(x_(300))=0.128309f\left(x_{300}\right)=0.128309f(x300)=0.128309 M229≈v299(x300)=0.144181M229≈v299x300=0.144181M_(229)~~v^(299)(x_(300))=0.144181M_{229} \approx v^{299}\left(x_{300}\right)=0.144181M229≈v299(x300)=0.144181
The errors are in this case
1.G.ARONSSON,Extension of functions aatisfying Lipschits con- ditions ,Arkiv ior Matheratik 6, 28 (1967),551-561.
2.J.CZIPSER and I.GEHER,Ritersion of functions satisfying a Iipschitz condition,Acta.Math.Acad.Sci,Hungar 6 (1955), 213-220.
3.B.LEVY and M.D.RICE ,The Approximation of Uniformly Continuous Mappings by Lipschitz and Hölder Mappings,(preprint),1980.
4.E.J.McSHANS,Extension of range of functions,Bull,Amer.Math. Soc. 40 (1934),837-842.
5.O.MUSTATA,Best Approximation and Unique Extension of Lipachits Functions,Journal Approx.Theory 19 (1977),222-230.
6.B.SHUBERT,A sequential aethod seeking the global maximum of a function,SIAM J.Humer.Anal.9(1972), 379−388379−388379-388379-388379−388.
7.The Otto Dunkel Memorial Problem Book,New Yort(1957), Normal cone valued metrics and nonconvex vector