In RS as well as in SGS the authors are concerned with a problem of type (1). It reads:

The exact solution is known. It reads

Among other phenomena, this problem models conductive heat transfer with nonlinear heat generation.

It is important to state that Chebfun works in the physical (values) space, i. e., computes the nodal values of a solution in the nodes $x_j$ defined by (3). At the same time it computes the values of the coefficients of the solution expansion in phase (coefficients) space. The latter reads

where $T_k\left(x\right)$ are the usual Chebyshev polynomials and $N$ is the length of the solution provided by Chebfun.

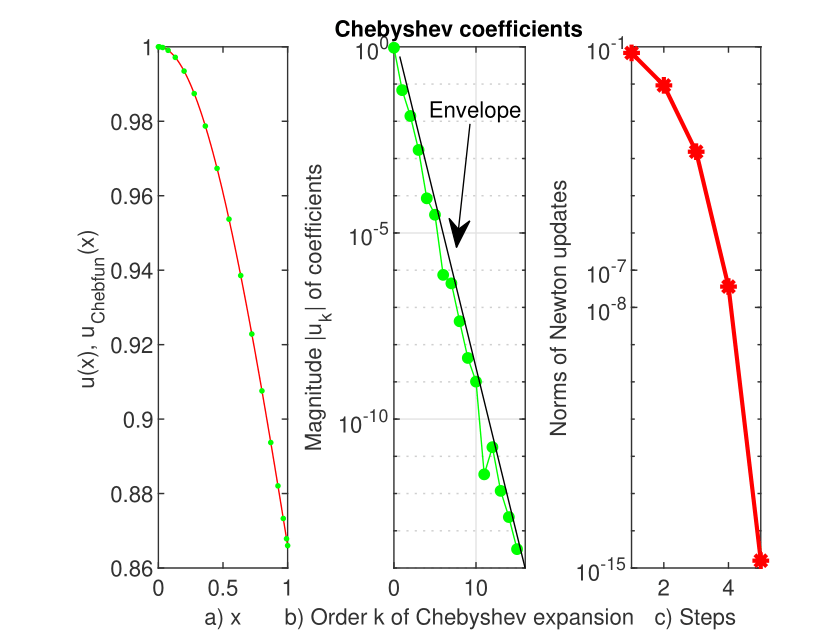
The Chebfun solution to this problem is depicted in panel a) of Figure 1. It is clear that it perfectly overlaps with the exact solution. The error in the $inf$ norm is of the order ${10}^{-15}$.

The second panel of this figure shows that the Chebyshev coefficients of the solution decrease almost linearly to the machine precision and the length of solution is $N=16$. A straight line which bounds them from above, the so called envelope, is also drawn. This parallelizes the straight line through origin of the equation

where $m\simeq -1.$ It means that the (asymptotic) rate of convergence of Chebfun is exponential or geometric (see the monograph JPB , Chapter 2 for the definition of the rate of convergence).

From panel c) of the same figure we understand that the Newton method is of the second order and uses five iterations.

Chebfun provides precise details on the accuracy with which the boundary conditions are enforced. In this case the residue vanishes.

In RS a classic method with finite differences is used in order to solve this problem and the authors expect an accuracy of order ${10}^{-4}.$ In a recent paper SGS the authors make use of the Haar wavelet method in order to solve a quasi-linearized version of this problem. Nor do they expect for better accuracy than something of order ${10}^{-6}.$

Finally we have solved the problem with MATLAB’s $bvp4c$ routine (see KS for this routine). In this case we could not find the solution with an error better than ${10}^{-5}.$

Due to limited space, we will not be able to repeat and report all these comparisons for every problem which follows. However, we will sum up conclusions in the last Section.

In GGL the authors consider a problem of type (1) in which the nonlinear term $f$ satisfies the so called Bernstein growth condition. Actually it means that $f$ can grow at most quadratically in its derivative variable.

We will consider the following example from this paper:

The Chebfun solution to this problem is depicted in panel a) of Figure 2. This has exactly the same shape as the one obtained in GGL by shooting along with continuation with respect to the initial data. The Newton’s method in solving the Chebfun discretization has second order (see panel b)) and the coefficients of Chebfun solution decrease smoothly and linearly to the level of machine precision. The convergence of the method remains exponential but the slope $m$ approximately equals $-0.3$ in (7), i.e., less optimal than in the previous example.

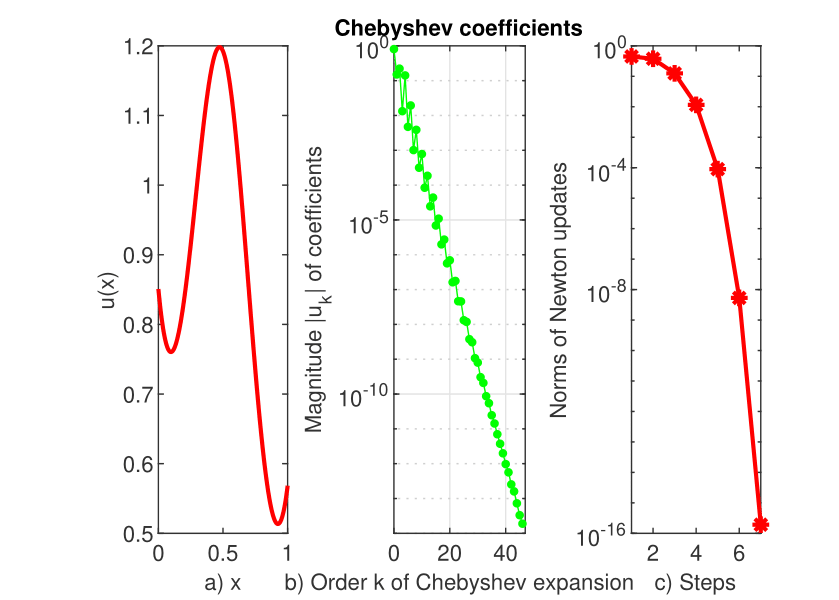
We have intentionally chosen this example from the paper quoted above to show that the enforcement of mixed conditions is extremely simple in Chebfun and especially very precise, i.e., the final error in solving them is of order ${10}^{-11}$. Such an estimate is practically impossible with conventional ChC or $bvp4c$.

The equations of Lane-Emden-Fowler type arise in various applications in mechanics, nuclear physics, gas-dynamics, stellar structures, and chemically reacting systems. In Gorder the author considers the nonlinear ODE

supplied with boundary conditions

or

For $k=0$ and $\epsilon >0$ the problem (9)-(10) admits the following exact first integral

where $-1\le x_1\ne x_2\le 1$ and $ℰ𝒾\left(x\right)$ denotes the exponential integral $ℰ𝒾\left(x\right):={\int }_{-\mathrm{\infty }}^x\frac{e^t}{t}𝑑t.$

In order to see how accurate this integral is satisfied we take first $x_1:=1$ and $x_2:=0$ and then from the boundary conditions we introduce $u\left(x_1\right)=0$ and $u^{\prime }\left(x_2\right)=0$ (the symmetry of solution with respect to $x$). The values $u^{\prime }\left(x_1\right)$ and $u\left(x_2\right)$ have been computed by Chebfun.

Thus, in our computation, regardless of the values of parameters $\delta$ and $\epsilon$, the first integral (12) is satisfied with a precision of order ${10}^{-13}.$

Chebfun has no difficulty solving problems (9)-(10) and (9)-(11). The solutions to the problem (9)-(10) are displayed in Figure 3. The Newton method has effectively second order and no more than two or three iterations are used in each case.

The convergence of the method is exponential with the slope $m$ approximately equaling $-0.3$ in (7). Improper integrals

in the first integral (12) are also calculated without any difficulty by Chebfun. It uses $sum$ operator along with option ${}_{}{}^{\prime }splittin{g}^{\prime }{,}^{\prime }o{n}^{\prime }.$ In each case the Newton process started from the initial guess $u_0:=1$.

In Agarwal, O’Regan (2003) the authors consider the existence issue for the problem

where The case $\nu :=1$ corresponds to the Newtonian fluid.

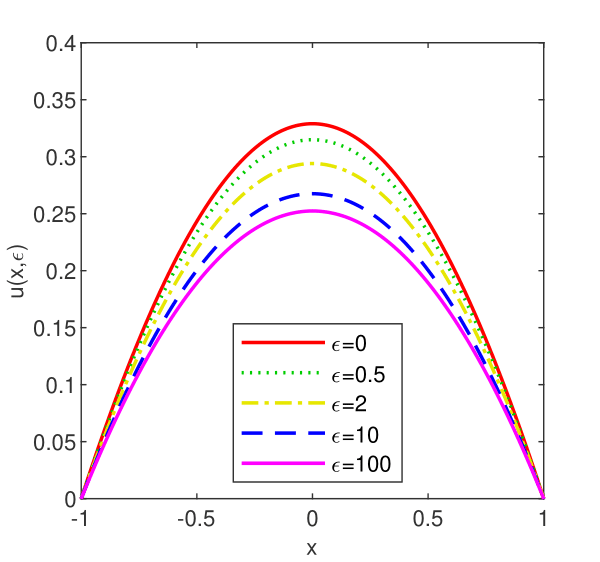
This problem is much more difficult than the previous one in the following sense. If in the previous case Chebfun used a tolerance of order ${10}^{-14}$ for Newton’s solver in this case we had to loosen this tolerance to ${10}^{-6}$ in order to guarantee a convergent procedure.

A set of solutions to problem (13) is displayed in Figure 4.

In the left panel of Figure 5 we display the norm of Newton’s updates vs. iteration number in the worst case, i.e. $\nu =1/2$. It is apparent that the order of the Newton’s method is much less than $2$.

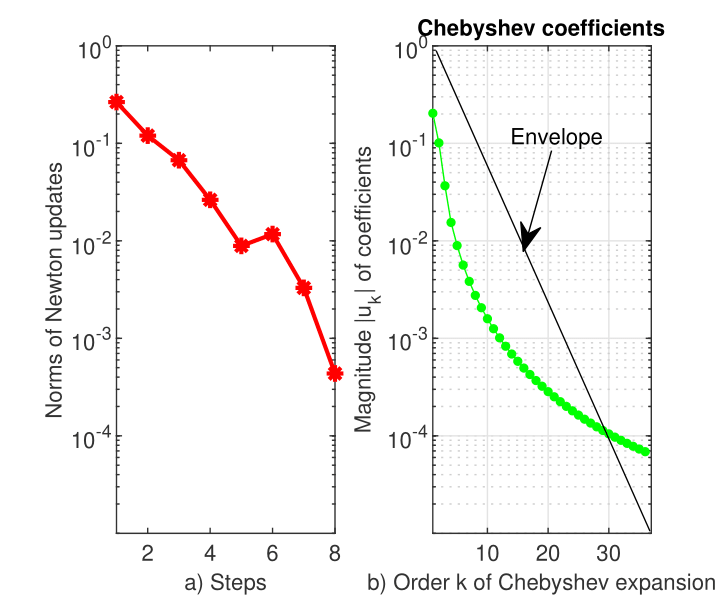
From the right panel of Figure 5 we see that the solution has length $37$ and its coefficients decrease smoothly but remain very far from the machine precision level. We also drew the envelope for these coefficients and from the log-linear plot b) of Figure 5 we can only infer that asymptotically, i.e. for large $k$, the coefficients of expansion (6) of solution satisfy

which means that the rate of convergence is only algebraic.

The point where the envelope intersects the coefficients’ curve is (roughly!) the magnitude of the error. In fact, the coefficients decrease slightly below the level ${10}^{-4}.$

The problem of finding an initial guess in order to ensure the convergence of Newton’s iterates is not at all simple in this case. Repeated attempts led us to an initial date of the form

This initial guess satisfies the boundary conditions of problem (13) and has a curvature close to that of numerical outcomes.

It should be noted that for values of the parameter $\nu$ in the range $(0,1/2)$ Chebfun completely failed!

In order to solve this problem for arbitrary values of $\nu$ in FLP the authors have introduces an iterative technique which reduces the problem to a sequence of usual eigenvalue problems. We have tested the capabilities of Chebfun in solving various Sturm-Liouville problems in some previous papers thus we are not interested in these iterative techniques (see for instance our contribution CIG2021 ).

The analytical study of the problem

has been initiated in DG . Roughly speaking in this model the right hand side is the heat production rate per unit volume, $u\left(x\right)$ is the absolute temperature, $x$ is the radial distance from the centre, $a$ is the inverse of the average thermal conductivity inside the head and $b$ is a heat exchange coefficient.

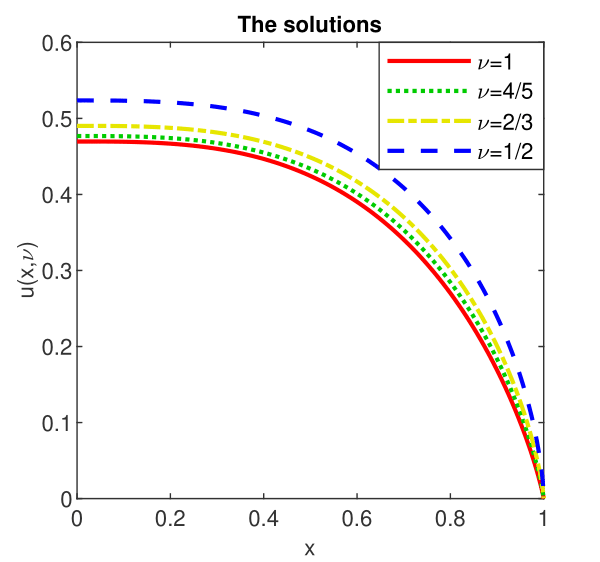
Three solutions $u(x,a,b)$ of this problem are reported in the panel a) of Figure 6.

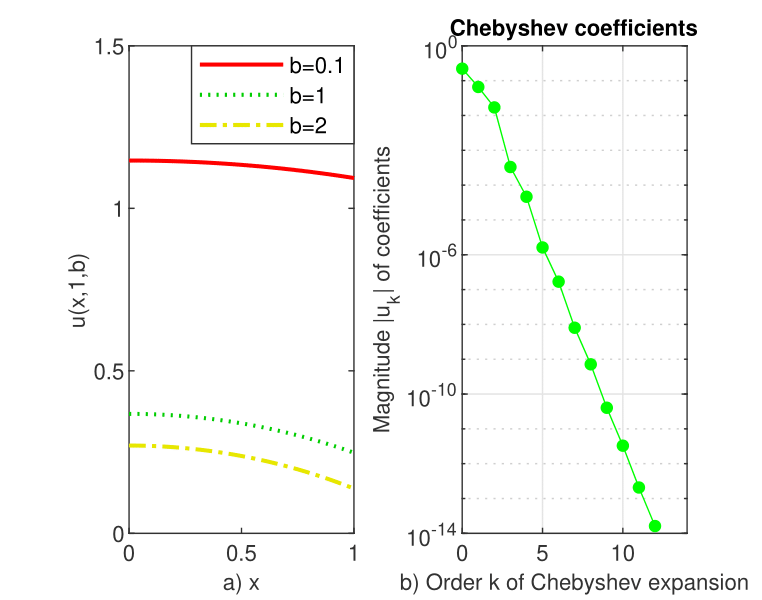
The behavior of Chebyshev coefficients in the panel b) of Figure 6 shows that the rate of convergence is definitely exponential.

Although the problem has received some attention over time, we have not found numerical results with which to compare ours. In any case, in its solution Newton’s method keeps the second order and does not use more than six iterative steps.

In CRK the authors consider, among other problems, the following nonlinear and singular problem:

which describes a flat, circular elastic membrane which is deformed by an axisymmetric pressure applied to its surface. The edge of the membrane is restrained from deforming normal to its mid-plane. Either a compressive radial thrust or a contractile radial displacement is applied to the edge. The dependent variable $u\left(x\right)$ stands for the radial stress and $x$ is the dimensionless radius. The parameter $\nu$ stands for Poisson ration of the membrane material.

Two solutions to the problem (15) are displayed in Figure 7.

The calculation of the two solutions differs fundamentally. In the first case ($\nu =1/2$) Chebfun produces the solution in five iterations and the Newton’s method has the second order. In the other case, Chebfun produces the solution in $86$ iterations and the order of Newton’s method is far from order two. This aspect is visible in the left panel of Figure 8.

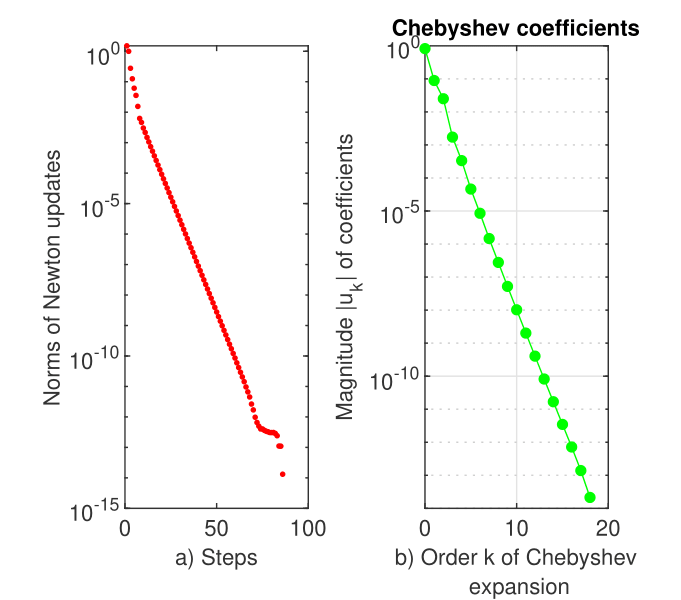
The behavior (almost linear decrease to the machine precision level) of the Chebyshev coefficients of the solution suggests a still exponential convergent process (see the b) panel in Figure 8).

One remark is suitable at this stage. For lower values of Poison parameter (membrane made of stiffer materials) Chebfun simply failed.

Our observations from many numerical experiments lead us to the conclusion that singularity is more difficult to manage than non-linearity for Chebfun. In order to strengthen this assertion we consider another example.

Thus, in Agarwal, O’Regan (1998) the authors are concerned the singular and non-linear problem:

Three solutions of this problem are displayed in the panel a) of Figure 9.

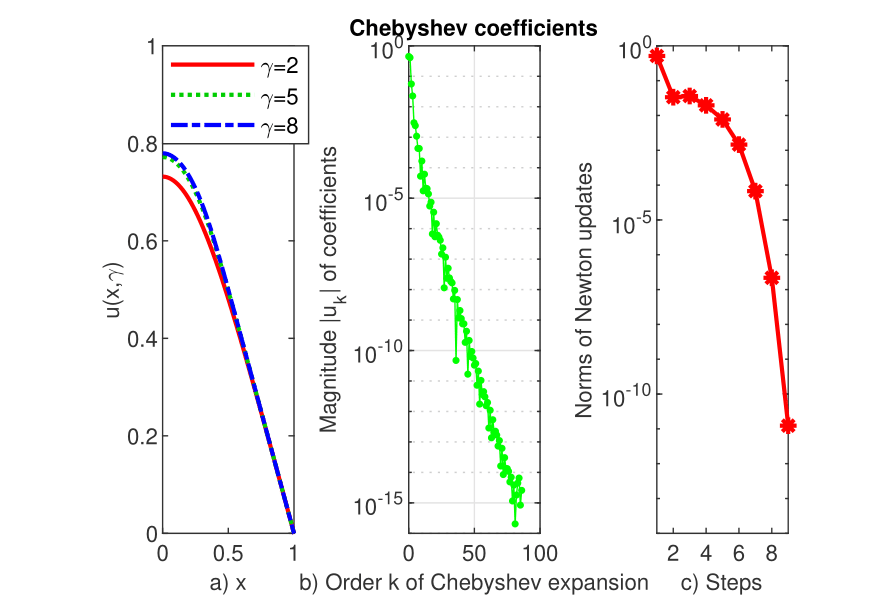
For higher values of $\alpha$ than $1$, Chebfun could not solve the problem even though the tolerance was considerably lower. This is not the case for the exponent $\gamma$.

For the highest value of $\gamma$ the convergence rate remains exponential and the Newton’s method has an order close to two. These result from panels b) and c) of the same figure.

In MS the authors analyze the following problem:

Five solutions of this problem are reported in Figure 10. They correspond to

and confirm that there exists a sharp boundary layer at the right of $x=0.$

In order to reach the lowest value $\epsilon :={10}^{-5}$ we have used continuation with respect to this parameter and we have loosen the tolerance to ${10}^{-10}.$ As a result, the convergence of the Newton method is no longer quadratic but is reduced to something around the unit.

It is very important to underline that for $\epsilon :={10}^{-1}$ Chebfun uses a solution of length $97$ and for $\epsilon :={10}^{-5}$ it uses a much larger solution of length $2508.$ The Newton’s method resolved the first case mentioned above using $7$ iterations while for the later case it resolved the problem only in four iterations. The order of the Newton method is close to two, but the Chebyshev coefficients of the solution decrease only to the level ${10}^{-11}.$

We have not found numerical results in the literature to compare with ours. Some other listed problems in MS have been solved by Chebfun without any difficulty.

The exact solution to (17) has the form:

When $\epsilon :={10}^{-5},$ the $inf$ $norm$ of the error

reaches the value of order ${10}^{-5}$ which emphasizes the accuracy of the computations.