Abstract
This article presents a new approach to solve the equations of flow in heterogeneous porous media by using random walks on regular lattices. The hydraulic head is represented by computational particles which are spread globally from the lattice sites according to random walk rules, with jump probabilities determined by the hydraulic conductivity. The latter is modeled as a realization of a random function generated as a superposition of periodic random modes. One- and two-dimensional numerical solutions are validated by comparisons with analytical manufactured solutions. Further, an ensemble of divergence-free velocity fields computed with the new approach is used to conduct Monte Carlo simulations of diffusion in random fields. The transport equation is solved by a global random walk algorithm which moves computational particles representing the concentration of the solute on the same lattice as that used to solve the flow equations. The integrated flow and transport solution is validated by a good agreement between the statistical estimations of the first two spatial moments of the solute plume and the predictions of the stochastic theory of transport in groundwater.
Authors
Nicolae Suciu, Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy
Keywords
global random walk; flow in heterogeneous porous media; Monte Carlo simulations.
References
Cite this paper as:
N. Suciu, Global Random Walk Solutions for Flow and Transport in Porous Media, in: Numerical Mathematics and Advanced Applications ENUMATH 2019, pp. 939-947, doi: https://doi.org/10.1007/978-3-030-55874-1_93
About this paper
Journal
Springer
Publisher Name
Print ISSN
Not available yet.
Online ISSN
Google Scholar Profile
Cauerstraße. 11, 91058 Erlangen, Germany, 11email: suciu@math.fau.de
Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy,
Fantanele 57, 400320 Cluj-Napoca, Romania
Global Random Walk Solutions for Flow and
Transport in Porous Media
Abstract
This article presents a new approach to solve the equations of flow in heterogeneous porous media by using random walks on regular lattices. The hydraulic head is represented by computational particles which are spread globally from the lattice sites according to random walk rules, with jump probabilities determined by the hydraulic conductivity. The latter is modeled as a realization of a random function generated as a superposition of periodic random modes. One- and two-dimensional numerical solutions are validated by comparisons with analytical manufactured solutions. Further, an ensemble of divergence-free velocity fields computed with the new approach is used to conduct Monte Carlo simulations of diffusion in random fields. The transport equation is solved by a global random walk algorithm which moves computational particles representing the concentration of the solute on the same lattice as that used to solve the flow equations. The integrated flow and transport solution are validated by a good agreement between the statistical estimations of the first two spatial moments of the solute plume and the predictions of the stochastic theory of transport in groundwater.
1 Introduction
Global random walk (GRW) algorithms, unconditionally stable and free of numerical diffusion, solve parabolic partial differential equations by moving computational particles on regular lattices according to random walk rules Vamosetal2003 . The GRW approach, intensively used in Monte Carlo simulations of diffusion in random velocity fields Suciu2014 , is based on the relationship between the ensemble of trajectories of the diffusion process governed by the Itô equation and the probability density of the process which verifies a Fokker-Planck equation. The strength of the approach is that instead of sequentially generating random walk trajectories one counts the number of particles at lattice sites, updated according to the binomial distributions which describe the number of jumps to neighboring lattice sites. Since the total number of particles is arbitrarily large, one obtains in this way highly accurate numerical approximations of the probability density, which, in case of transport simulations, is the normalized concentration of the solute that is transported by advection and diffusion.
The second order differential operator of the Fokker-Planck equation coincides with the diffusion operator in the mass balance equation with closure given by the Fick’s law only if the diffusion coefficient is constant. Otherwise, in order to rewrite the diffusion equation as a Fokker-Planck equation, the drift coefficients have to be augmented with the spatial derivatives of the diffusion coefficients (e.g., (Suciu2019, , Sect. 4.2.1)). The same procedure can be used to write the pressure equation for flow in porous media based on Darcy’s law (e.g., Raduetal2011 ) as a Fokker Planck equation. Further, numerical solutions of the flow problem can be obtained by solving the problem formulated for the equivalent Fokker-planck equation by GRW methods.
In case of highly variable coefficients, the particles may jump over several lattice sites, the variability of the coefficients is smoothed, and the GRW solutions are affected by overshooting errors SuciuandVamos2006 . Such errors are avoided by using biased-GRW algorithms, where the particles are only allowed to jump to neighboring sites and the advective displacements are accounted for by biased jump probabilities that are larger in the direction of the drift (Suciu2019, , Sect. 3.3.3). A different remedy, appropriate for GRW solutions of the flow problem, consists of approximating directly the second order operator in diffusion form, with flux terms estimated at the middle of the lattice intervals by using staggered grids (Suciu2019, , Sect. 3.3.4.1).
We consider a two-dimensional domain, and the pressure equation for flow in saturated porous media with constant porosity,
| (1) |
where is the hydraulic head, is an isotropic hydraulic conductivity, and is a source/sink term. For an arbitrary initial condition (IC) and time independent boundary conditions (BC), the non-steady solution of Eq. (1) approaches a stationary hydraulic head . With and BC given by
| (2) | ||||
| (3) |
the gradient of the hydraulic head determines the components of the divergence-free velocity field according to Darcy’s law
| (4) |
The GRW solutions presented in the following are tested against analytical manufactured solutions Roache2002 obtained from data files and codes given in the Git repository https://github.com/PMFlow/FlowBenchmark. The isotropic hydraulic conductivity is a space random function with mean m/day. The random fields are normally distributed, with Gaussian correlations of fixed correlation length m and increasing variances , with realizations generated as sums of a finite number of cosine random modes (Suciu2019, , Appendix C.3.1.2).
2 One-dimensional GRW algorithms
The three different GRW approaches discussed in Section 1 are tested in the following by solving the one-dimensional (1D) version of Eq. (1) written as an advection-diffusion equation,
| (5) |
in the interval , . The source and the BCs and are determined by the manufactured solution (see Git repository, /FlowBenchmark/Manufactured_Solutions/Matlab/Gauss 1D/). The precision of the numerical solution is quantified by the discrete norm .
GRW algorithms approximate the hydraulic head by the distribution at lattice sites and times of a system of random walkers, . The unbiased GRW moves groups of particles on the lattice according to
| (6) |
| (7) |
where is the floor function, , , are discrete advective displacements, and is the amplitude of the diffusive jumps. The time step and the space step are related by
| (8) |
where , , is a variable jump probability. The number of particles undergoing diffusion jumps, , and the number of particles waiting at over the time step, , are binomial random variables with mean values given by (Suciu2019, , Sect. 3.2.2)
In the biased GRW algorithm and Eq. (6) is replaced by
The quantities verify in the mean
where . The biased jump probabilities are given by with defined by (8) and, in addition to , one imposes the constraint (Suciu2019, , Sect. 3.3.3).
Alternatively, a GRW solution of the 1D version of the pressure equation (1),
can be obtained as steady-state limit of the staggered finite difference scheme
With jump probabilities defined by , , the staggered scheme becomes
| (9) | |||||
The contributions to lattice sites from neighboring sites summed up in (9) are obtained with the GRW algorithm which moves particles from sites to neighboring sites according to
| (10) |
For consistency with the staggered scheme (9), the quantities in (11) have to satisfy in the mean (Suciu2019, , Sect. 3.3.4.1),
| (11) |
The three GRW algorithms from above approximate the binomial random variables by rounding of the unaveraged relations for the mean, e.g., (11), summing up the reminders of multiplication by and of the floor function , and allocating a particle to the lattice site where the sum reaches the unity. By giving up the particle indivisibility, one obtains deterministic GRW algorithms which represent the solution by real numbers and use the anaveraged relations for .
Since the unbiased GRW algorithm is prone to large overshooting errors, due to the high variability of the coefficients and , it is not appropriate to solve the flow problem. For instance, to solve the test problem for with errors , an extremely small step is needed and one time iteration takes about 8 minutes. Efficient solutions can be obtained with the biased GRW algorithm (Method 1) and the GRW on staggered grids in both the random (Method 2) and the deterministic implementation (Method 3). The stationary regime of the GRW simulations, indicated by constant total number of particles and error (see Fig 1), is reached after time iterations. The comparison shown in Table 1 indicates that the deterministic implementation of the GRW on staggered grids is the most efficient approach to solve flow problems for heterogeneous porous media.
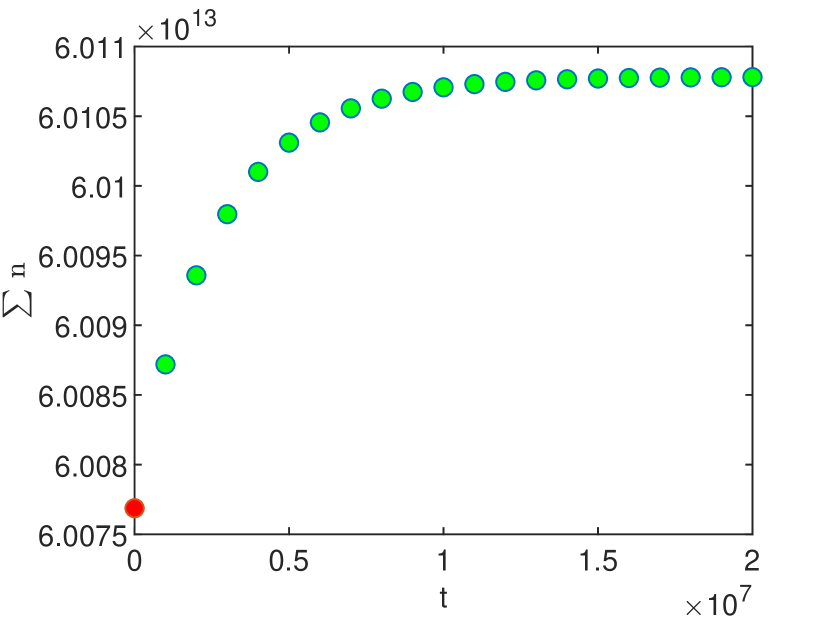
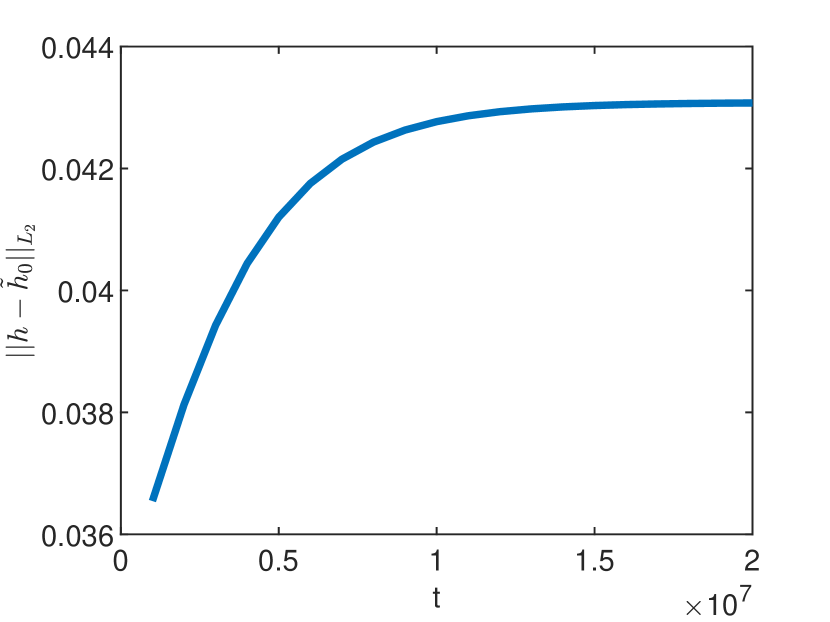
| Method 1 | Method 2 | Method 3 | |
| 4.31e-02 | 1.60e-2 | 1.60e-02 | |
| CPU (min) | 37.12 | 14.03 | 6.48 |
3 Two-dimensional GRW solutions of the flow problem
The problem (1-3), with , , , , and IC given by the manufactured solution, , is solved by the deterministic GRW on staggered grids. The errors with respect to the manufactured solution are shown in Table 2.
| 3.12e-02 | 4.08e-02 | 1.35e-01 | |
| 2e06 | 1e07 | 2e07 | |
| CPU (min) | 11.26 | 55.49 | 111.54 |
The convergence of the 2D GRW solutions is investigated for the homogeneous problem (, and IC given by the constant slope ), for increasing , by successively halving the step size five times from to . Using the errors with respect to the solution on the finest grid, , the estimated order of convergence (EOC) is computed according to . The results presented in Table 3 indicate the convergence of order 2 for all the three values of .
| EOC | EOC | EOC | EOC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2.78e-03 | 1.9979 | 6.96e-04 | 2.0167 | 1.72e-04 | 2.0687 | 4.10e-05 | 2.3219 | 8.20e-06 | |
| 2.63e-03 | 1.9902 | 6.62e-04 | 2.0131 | 1.64e-04 | 2.0685 | 3.91e-05 | 2.3219 | 7.82e-06 | |
| 2.67e-03 | 1.9839 | 6.75e-04 | 2.0150 | 1.67e-04 | 2.0654 | 3.99e-05 | 2.3219 | 7.98e-06 |
4 Statistical inferences
A Monte Carlo ensemble of solutions is obtained by solving the 2D homogeneous problem () for 100 realizations of the random -field with fixed . A realization of the hydraulic head is shown in Fig 2. The components of the velocity field computed according to Darcy’s law (4) are shown in Fig. 3.
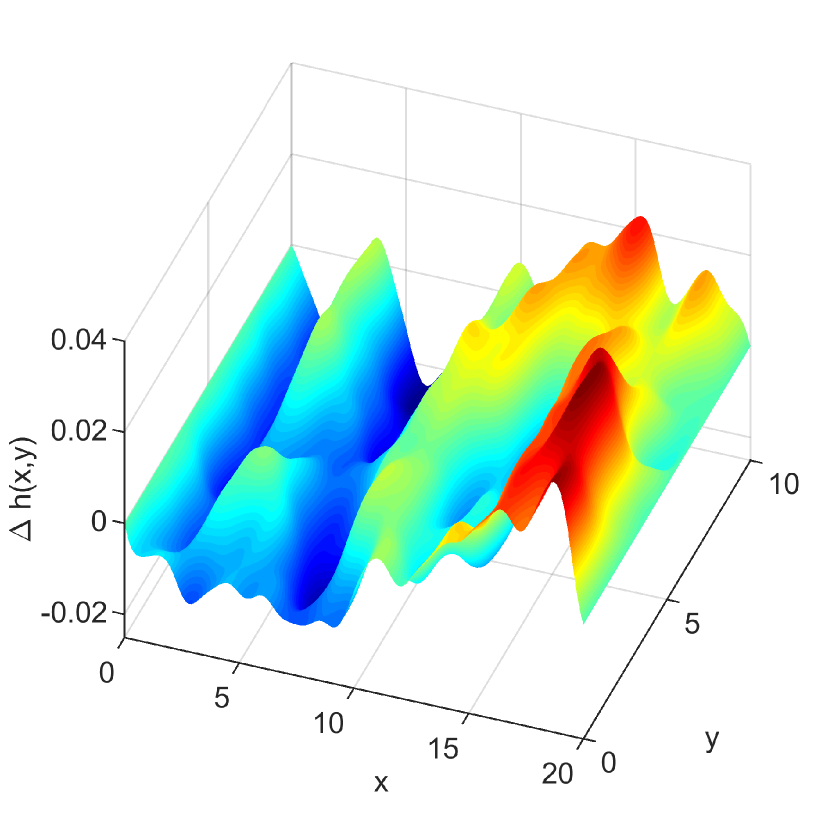

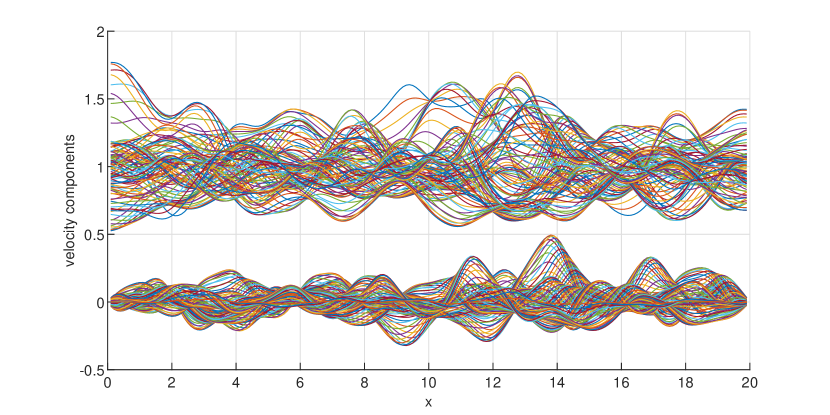
The Monte Carlo estimates presented in Table 4 are close to the first-order theoretical predictions of the stochastic theories of flow and transport in groundwater Dagan1989 , e.g. variances of the order for the hydraulic head, , and , for longitudinal and transverse velocity components, respectively.
| mean | 5.00e-01 1.74e-01 | 9.98e-01 1.91e-02 | -7.32e-04 1.24e-02 |
| variance | 3.27e-04 6.27e-05 | 3.68e-02 5.50e-03 | 1.30e-02 1.90e-03 |
5 Validation of the flow and transport GRW solutions
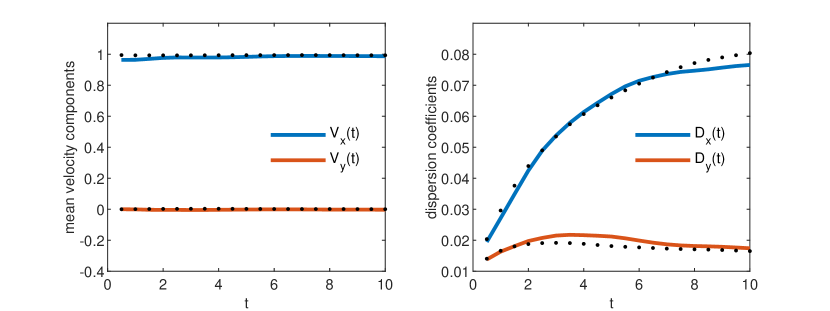
The numerical setup from Section 4 corresponds to a possible scenario of contaminant transport in groundwater systems with low heterogeneity Suciu2014 . With a typical value of the local dispersion coefficient m2/day, Monte Carlo simulations of advection-diffusion are carried out using the ensemble of 100 velocity fields, on the same lattice as that used in Section 4 to solve the flow problem. The transport problem is solved with the 2D generalization of the unbiased GRW algorithm (6-7) (Suciu2019, , Appendix A.3.2). The Monte Carlo estimates of the velocity of the plume’s center of mass and of the effective dispersion coefficients presented in Fig. 4 are in good agreement with the first-order results obtained from simulations using a linear approximation of the velocity field (Suciu2019, , Appendix C.3.2.2).
References
- (1) Dagan, G.: Flow and Transport in Porous Formations. Springer, Berlin (1989) https://doi.org/10.1007/978-3-642-75015-1
- (2) Radu, F.A., Suciu, N., Hoffmann, J., Vogel, A., Kolditz, O., Park, C-H., Attinger, S.: Accuracy of numerical simulations of contaminant transport in heterogeneous aquifers: a comparative study. Adv. Water Resour. 34, 47–61 (2011) http://dx.doi.org/10.1016/j.advwatres.2010.09.012
- (3) Roache, P.J.: Code verification by the method of manufactured solutions. J. Fluids Eng. 124 (1):4–10 (2002) http://dx.doi.org/10.1115/1.1436090
- (4) Suciu, N.: Diffusion in random velocity fields with applications to contaminant transport in groundwater. Adv. Water Resour. 69 (2014) 114-133. http://dx.doi.org/10.1016/j.advwatres.2014.04.002
- (5) Suciu, N.: Diffusion in Random Fields. Applications to Transport in Groundwater. Birkhäuser, Basel (2019) https://doi.org/10.1007/978-3-030-15081-5
- (6) Suciu, N., Vamoş, C.: Evaluation of overshooting errors in particle methods for diffusion by biased global random walk. Rev. Anal. Num. Th. Approx. (Romanian Academy) 35, 119–126 (2006) https://ictp.acad.ro/jnaat/journal/article/view/2006-vol35-no1-art17
- (7) Vamoş, C., Suciu, N., Vereecken, H.: Generalized random walk algorithm for the numerical modeling of complex diffusion processes. J. Comput. Phys., 186, 527-544 (2003) https://doi.org/10.1016/S0021-9991(03)00073-1.
