On the monotonicity of the sequences of approximations obtained by Steffensen’s method

Ion Păvăloiu

In a recent paper [1], M. Bálazs studied the conditions in which the sequence $\left(x_{n}\right)_{n\geq 0}$ generated by Steffensen’s method is monotonic and converges to the solution of equation

(1)

f\left(x\right)=0

where $f:I\rightarrow\mathbb{R}$ is a given function, and $I\subset\mathbb{R}$ is an interval of the real axis. Paper [1] considers the simple case of the sequence generated by the recurrence relation

(2)

x_{n+1}=x_{n}-\tfrac{f\left(x_{n}\right)}{\left[x_{n},g\left(x_{n}\right);f% \right]},\qquad n=0,1,\ldots,x_{0}\in I,\

in which $g:I\rightarrow\mathbb{R}$ is given by $g\left(x\right)=x-f\left(x\right),$ and $\left[u,v;f\right]$ is the first order divided difference of the function $f .$

The following theorem is proved in [1]:

Theorem 1.

[1]. Let $f:I\rightarrow\mathbb{R}$ be a continuous function on $I,$ and define $g\left(x\right)=x-f\left(x\right).$ If the following conditions:

(i)

The function $g:I\rightarrow\mathbb{R}$ is strictly decreasing and convex on $I;$
(ii)

there exists a point $x_{0}\in I$ such that $f\left(x_{0}\right)<0;$
(iii)

$I_{0}=\left[x_{0}-d,\ x_{0}+d\right]\subset I,$ where $d=\max\{\left|f\left(x_{0}\right)\right|,\left|f\left(g\left(x_{0}\right)% \right)\right|\}$

hold, then all elements of the sequence $\left(x_{n}\right)_{n\geq 0}$ generated by (2) belong to $I_{0};$ in addition, the following properties hold:
(j)

the sequence $\left(x_{n}\right)_{n\geq 1}$ is increasing and convergent;
(jj)

the sequence $\left(g\left(x_{n}\right)\right)_{n\geq 1}$ is decreasing and convergent;
(jjj)

$\lim\limits_{n\rightarrow\infty}x_{n}=\lim\limits_{n\rightarrow\infty}g\left(x% _{n}\right)=x^{\ast},$ where $x^{\ast}$ is the unique solution of equation (1) in $I .$

We shall show further down that the properties resulting from Theorem 1 hold for more general Steffensen-type methods, while for the method (2), if hypothesis (ii) is replaced by:

(ii₁)

there exists $x_{0}\in I$ for which $f\left(x_{0}\right)>0$ and $g\left(x_{0}\right)\in I,$ then hypothesis (iii) can be dropped, and the conclusions of the theorem remain valid putting $I_{0}=\left[g\left(x_{0}\right),x_{0}\right].$

Consider an arbitrary function $g:I\rightarrow\mathbb{R}$ whose fixed points coincide with the real roots of equation (1), and reciprocally.

The following theorem holds:

Theorem 2.

If the functions $f:I\rightarrow\mathbb{R}$ and $g:I\rightarrow\mathbb{R}$ are continuous on $I,$ and if the following conditions:

(i₂)

the function $\ g$ is strictly decreasing on $I;$
(ii₂)

the function $f$ is strictly increasing and concave on $I;$
(iii₂)

there exists $x_{0}\in I$ such that $f\left(x_{0}\right)>0,\ g\left(x_{0}\right)\in I$ and $x_{0}-g\left(x_{0}\right)>0$
(iv₂)

the equations $f\left(x\right)=0$ and $g\left(x\right)=x$ are equivalent, are fulfilled then equation (1) has a unique solution $x^{\ast}\in\left[g\left(x_{0}\right),x_{0}\right]$ and the following properties hold:
(j₂)

the sequence $\left(x_{n}\right)_{n\geq 0}$ is decreasing and convergent;
(jj₂)

the sequence $\left(g\left(x_{n}\right)\right)_{n\geq 0}$ is increasing and convergent;
(jjj₂)

$\lim\limits_{n\rightarrow\infty}x_{n}=\lim\limits_{n\rightarrow\infty}g\left(x% _{n}\right)=x^{\ast},$ where $x^{\ast}$ is the unique solution of equation (1), therefore fixed point of $g$ in the interval $I .$

Proof.

From (2), for $n=1,$ we get

x_{1}-x_{0}=-\tfrac{f\left(x_{0}\right)}{\left[x_{0},g\left(x_{0}\right);f% \right]}<0,

that, is $x_{1}<x_{0}.$

Writing $h\left(x\right)=x-g\left(x\right),$ we have $h\left(x_{0}\right)>0$ by hypothesis; moreover:

h\left(g\left(x_{0}\right)\right)=g\left(x_{0}\right)-g\left(g\left(x_{0}% \right)\right)=\left[g\left(x_{0}\right),x_{0};g\right]\left(x_{0}-g\left(x_{0% }\right)\right)<0

hence the equation $h\left(x\right)=0$ has unique solution in the interval $\left[g\left(x_{0}\right),x_{0}\right],$ i.e. $g$ has a unique fixed point $x^{\ast}$ in this interval. Since the fixed points of $g$ coincide with the roots of equation (1) and reciprocally, there follows that $x^{\ast}$ is unique solution for equation (1) within the same interval, and $f\left(g\left(x_{0}\right)\right)<0.$ Now we shall show that $x_{1}>x^{\ast}.$ First show that $x_{1}>g\left(x_{0}\right).$

It is easy to verify that the terms of the sequence $\left(y_{n}\right)_{n\geq 0}$ provided by the relations

y_{n+1}=g\left(y_{n}\right)-\tfrac{f\left(g\left(y_{n}\right)\right)}{\left[y_% {n},g\left(y_{n}\right);f\right]},\qquad n=0,1,\ldots,y_{0}=x_{0}

coincide with those of the sequence $\left(x_{n}\right)_{n\geq 0}$ generated by (2). In other words the equalities

x_{n}-\tfrac{f\left(x_{n}\right)}{\left[x_{n},g\left(x_{n}\right);f\right]}=g% \left(x_{n}\right)-\tfrac{f\left(g\left(x_{n}\right)\right)}{\left[x_{n},g% \left(x_{n}\right);f\right]},\qquad n=0,1,\ldots

hold; for $n=0,$ it follows that:

x_{1}-g\left(x_{0}\right)=-\tfrac{f\left(g\left(x_{0}\right)\right)}{\left[x_{% 0},g\left(x_{0}\right);f\right]}>0

from which it results that $x_{1}\in\left[g\left(x_{0}\right),x_{0}\right].$

From Lagrange’s interpolating polynomial we get

	$\displaystyle f\left(x_{1}\right)=$	$\displaystyle f\left(x_{0}\right)+\left[x_{0},g\left(x_{0}\right);f\right]% \left(x_{1}-x_{0}\right)$
		$\displaystyle+\left[x_{1},x_{0},g\left(x_{0}\right);f\right]\left(x_{1}-x_{0}% \right)\left(x_{1}-g\left(x_{0}\right)\right)$

and, since $\left[x_{1},x_{0},g\left(x_{0}\right);f\right]<0,$ taking into account (2), it follows that $f\left(x_{1}\right)>0,$ that is, $x_{1}>x^{\ast}.$ Since the function $h$ is increasing, it results that $h\left(x_{1}\right)>0$ , i.e. $x_{1}-g\left(x_{1}\right)>0.$ Let us show that $g\left(x_{1}\right)\in\left[g\left(x_{0}\right),x_{0}\right].$ We have $g\left(x_{1}\right)-g\left(x_{0}\right)=\left[x_{0},x_{1};g\right]\left(x_{1}-% x_{0}\right)>0$ that is, $g\left(x_{0}\right)<g\left(x_{1}\right)<x^{\ast}<x_{1}<x_{0}.$

Repeating the above argument, putting $x_{k}=x_{0},\ k\in\mathbb{N}$ , and supposing that the hypotheses of Theorem 2 are fulfilled for $x_{k},$ we obtain:

g\left(x_{k}\right)<g\left(x_{k+1}\right)<x^{\ast}<x_{k+1}<x_{k}.

It results subsequently that the sequences $\left(x_{n}\right)_{n\geq 0}$ and $\left(g\left(x_{n}\right)\right)_{n\geq 0}$ fulfil the properties (j₂) and (jj₂) of Theorem 2 and, in addition, are bounded.

Write $\bar{u}=\lim\limits_{n\rightarrow\infty}g\left(x_{n}\right)$ and $\bar{v}=\lim\limits_{n\rightarrow\infty}x_{n};$ we obtain $\bar{u}=g\left(\bar{v}\right)$ and $\bar{u}\leq x^{\ast}\leq\bar{v}.$ Suppose that $\bar{u}<\bar{v},$ therefore $\bar{u}-\bar{v}<0$ . But $\bar{u}-\bar{v}=g\left(\bar{v}\right)-\bar{v}=-h\left(\bar{v}\right)\geq 0,$ since $\bar{v}\geq x^{\ast};$ this shows that $\bar{u}=\bar{v}=x^{\ast}.$

At limit (for $n\rightarrow\infty$ ), equalities (2) yield $f\left(x^{\ast}\right)=0,$ where the continuity of $f$ was also taken into account. ∎

Remark 1.

If we put in Theorem 2, $g\left(x\right)=x-f\left(x\right),$ since $g$ is decreasing, it follows that $f\left(x\right)=x-g\left(x\right)$ is increasing; since $g$ is convex, it follows that $\left[x,y,z;g\right]>0$ for every $x,y,z\in I,$ hence $\left[x,y,z;f\right]=-\left[x,y,z;g\right]<0,$ that is, $f$ is concave. From $f\left(x_{0}\right)>0$ it follows $x_{0}-g\left(x_{0}\right)>0,$ i.e. $x_{0}>g\left(x_{0}\right).$ In this case, Theorem 1 in which hypotheses (ii) and (iii) are replaced by (ii₂) is a consequence of Theorem 2.

The results of Theorem 2 are graphically illustrated in Figure 1.

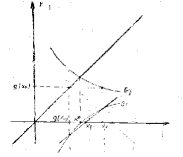
In what follows we shall present, without proof. other cases in which properties of monotonicity analogous to those given by Theorem 2 hold.∎

Theorem 3.

If the functions $f:I\rightarrow\mathbb{R}$ and $g:I\rightarrow\mathbb{R}$ are continuous on $I,$ and if the following conditions are fulfilled:

(i₃)

the function $\ g$ is strictly decreasing on $I;$
(ii₃)

the function $f$ is strictly increasing and convex on $I;$
(iii₃)

there exists $x_{0}\in I$ for which $f\left(x_{0}\right)<0,\ g\left(x_{0}\right)\in I$ and $x_{0}-g\left(x_{0}\right)<0;$
(iv₃)

the equations $f\left(x\right)=0$ and $x=g\left(x\right)$ are equivalent, then the sequence $\left(x_{n}\right)_{n\geq 0}$ generated by (2) is increasing and convergent, the sequence $\left(g\left(x_{n}\right)\right)_{n\geq 0}$ is decreasing and convergent, and $x^{\ast}=\lim\limits_{n\rightarrow\infty}x_{n}=\lim\limits_{n\rightarrow\infty% }g\left(x_{n}\right)$ is the solution of equation (1).

Figures 2 plots the results of Theorem 3.

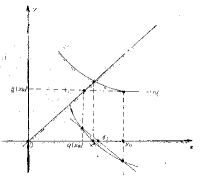
Theorem 4.

If the functions $f:I\rightarrow\mathbb{R}$ and $g:I\rightarrow\mathbb{R}$ are continuous on $I,$ and if the following conditions are fulfilled:

(i₄)

the function $g$ is strictly decreasing on $I;$
(ii₄)

the function $f$ is strictly decreasing and convex on $I;$
(iii₄)

there exists $x_{0}\in I$ for which $f\left(x_{0}\right)<0,\ g\left(x_{0}\right)\in I$ and $x_{0}-g\left(x_{0}\right)>0;$
(iv₄)

the equations $f\left(x\right)=0$ and $x=g\left(x\right)$ are equivalent, then the sequence $\left(x_{n}\right)_{n\geq 0}$ generated by (2) is decreasing and convergent, the sequence $(g\left(x_{n}\right))_{n\geq 0}$ is increasing and convergent, and $x^{\ast}=\lim\limits_{n\rightarrow\infty}x_{n}=\lim\limits_{n\rightarrow\infty% }g\left(x_{n}\right),f\left(x^{\ast}\right)=0.$

The results of this theorem are illustrated by Figure 3.

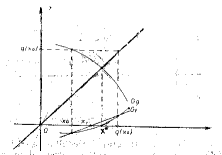
Theorem 5.

If the functions $f:I\rightarrow\mathbb{R}$ and $g:I\rightarrow\mathbb{R}$ are continuous on $I,$ and if the following conditions are fulfilled:

(i₅)

the functions $g$ is strictly decreasing on $I;$
(ii₅)

the function $f$ is strictly decreasing and concave on $I;$
(iii₅)

there exists $x_{0}\in I$ such that $f\left(x_{0}\right)>0,\ g\left(x_{0}\right)\in I$ and $x_{0}-g\left(x_{0}\right)<0;$
(iv₅)

the equations $f\left(x\right)=o$ and $x=g\left(x\right)$ are equivalent then the sequence $\left(x_{n}\right)_{n\geq 0}$ generated by (2) is increasing and convergent, the sequence $\left(g\left(x_{n}\right)\right)_{n\geq 0}$ is decreasing and convergent, and $\lim\limits_{n\rightarrow\infty}x_{n}=\lim\limits_{n\rightarrow\infty}g\left(x% _{n}\right)=x^{\ast},~{}f\left(x^{\ast}\right)=0.$

Remark 2.

The fact that the functions $f$ and $g$ from the above theorems are related only by the equivalence of equations $f\left(x\right)=0$ and $x=g\left(x\right)$ offers large possibilities to choose these functions (i.e. to choose $g$ when $f$ is known, and conversely).

It is clear that if $f$ keeps the same monotonicity and convexity on $I,$ then we can moot the question of determining a real number $\lambda$ such that $g\left(x\right)=x-\lambda f\left(x\right)$ be a decreasing function. Under certain conditions $\lambda$ can be determined, as it results from the following example:

If $f$ is strictly increasing and strictly convex on $I=\left[a,b\right],$ and if $f$ is differentiable, then $f^{\prime}$ is also derivable, and $f^{\prime}\left(x\right)>f^{\prime}\left(a\right)>0$ for every $x\in\left[a,b\right].$ Then we can put $g\left(x\right)=x-f\left(x\right)/f^{\prime}\left(a\right),$ and we have $g^{\prime}\left(x\right)\leq 0$ for every $x\in\left[a,b\right],$ hence $g$ is decreasing. It is clear that the equations $f\left(x\right)=0$ and $x=g\left(x\right)$ have the same roots. If $f\left(a\right)<0$ and $a-\frac{f\left(a\right)}{f^{\prime}\left(a\right)}<b,$ then it is obvious that $a-g\left(a\right)=\frac{f\left(a\right)}{f^{\prime}\left(a\right)}<0,$ and Theorem 3 can be applied for $x_{0}=a.$ ∎

Numerical example.

Consider the equation:

f\left(x\right)=x-\arcsin\tfrac{x-1}{\sqrt{2\left(x^{2}+1\right)}}=0,\ (x\in-% \infty,-1]

and the function $g$ given by the relation:

g\left(x\right)=\arcsin\tfrac{x-1}{\sqrt{2\left(x^{2}+1\right)}}

Since $g^{\prime}\left(x\right)=-\frac{1}{x^{2}+1}$ and $g^{\prime\prime}\left(x\right)=\frac{2x}{\left(x^{2}+1\right)^{2}}$ it follows that $g$ is decreasing on $(-\infty,-1],$ and $f$ is increasing and convex. One shows by direct calculation that $f\left(-2\right)\simeq-0.75$ $<0$ and $g\left(-2\right)\simeq-1.25,$ hence $f$ fulfils the hypotheses of Theorem 3. The table below lists the results of the calculations for $x_{0}=-2.$

${\footnotesize n}$	${\footnotesize x}_{n}$	${\footnotesize g}\left(x_{n}\right)$	${\footnotesize f}\left(x_{n}\right)$
0	-2.000000000000000000	-1.249045772398254430	-0.750954227601745574
1	-1.414047729532868260	-1.400933154002817630	-0.013114575530050630
2	-1.404227441155695550	-1.404222310683232820	-0.000005130472462734
3	-1.404223602392559510	-1.404223602391771120	-0.000000000000788388
4	-1.404223602391969620	-1.404223602391969620	-0.000000000000000000

Table 1.

The numerical results agree with the conclusions of Theorem 3; as one can see, after four iteration steps a solution approximation with 18 decimals is obtained (obviously, if truncation and rounding errors are neglected).∎

References

[1] Balázs, M., ^†^†margin: clickable $\rightarrow$ A bilateral approximating method for finding the real roots of real equations. Rev. Anal. Numér. Théor. Approx., 21, no. 2, 111–117, (1992).

[2] ^†^†margin: clickable $\rightarrow$ Păvăloiu, I., Sur la methode de Steffensen pour la résolution des équations operationnelles non lineaires, Revue Roumaine des Mathematiques Pures et Appliquees, XIII, 6, 149–158 (1968).

[3] Păvăloiu, I., ^†^†margin: clickable $\rightarrow$ Rezolvarea ecuaţiilor prin interpolare, Ed. Dacia, Cluj-Napoca (1981).

[4] Ul’m, S., Ob obobschenie metoda Steffensen dlya reshenia nelineinyh operatornyh uravnenii, Jurnal Vicisl, mat. i. mat-fiz. 4, 6, (1964).

Received 18.VI.1992

Institutul de Calcul al Academiei

Filiala Cluj

3400 Cluj-Napoca

Romania

On the monotonicity of the sequences of approximations obtained by Steffensen’s method

Abstract

Author

Keywords

PDF

Cite this paper as:

About this paper

Journal

Publisher Name

DOI

Print ISSN

Online ISSN

References

Paper (preprint) in HTML form

On the monotonicity of the sequences of approximations obtained by Steffensen’s method

Theorem 1.

Theorem 2.

Proof.

Remark 1.

Theorem 3.

Theorem 4.

Theorem 5.

Remark 2.

Numerical example.

References

Related Posts