Abstract
We solve by Laguerre collocation method two second order genuinely nonlinear singularly perturbed boundary value problems and a fourth order nonlinear one formulated on the half-line. First, we are concerned with solutions to a model equation for low Reynolds number flow, the so-called Cohen, Fokas, Lagerstrom model. Then we compute monotonously increasing solutions, the so-called “bubble type solutions”, to density profile equation for the description of the formation of microscopical bubbles in a nonhomogeneous fluid. We compare the results obtained in the latter case with those carried out by shooting or polynomial collocation both coupled with domain truncation. A fourth order nonlinear boundary value problem supplied with mixed boundary conditions in origin as well as at infinity is also solved. The solution and its first three derivatives are obtained and compared with their counterparts obtained by Keller’s box scheme. The collocation based on Laguerre functions avoids the domain truncation, exactly impose any kind of boundary conditions at infinity and resolve with reliable accuracy the sharp interior or exterior layer of the solutions. The method is fairly easy implementable and efficient in treating various types of nonlinearities. The accuracy of the method is also tested on the classical Blasius problem (a third order one). We solve with the same method the eigenvalue problem obtained by linearization around the constant solution, which corresponds to the case of a homogeneous fluid (without bubbles), and observe that this solution is stable.
Authors
Călin-Ioan Gheorghiu
(Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy)
Keywords
Singular nonlinear BVPs; collocation Laguerre functions; semi-infinite domain; Blasius problem; low Reynolds number flows; density profile equation; foundation engineering problem.
References
See the expanding block below.
Cite this paper as
C.I. Gheorghiu, Pseudospectral solutions to some singular nonlinear BVPs. Applications in nonlinear mechanics. Numer. Algor., 68 (2015) 1-14.
doi: 10.1007/s11075-014-9834-z
http://www.win.tue.nl/~hochsten/pdf/lame.pdf
About this paper
Print ISSN
1017-1398
Online ISSN
1572-9265
Google Scholar Profile
google scholar link
Paper (preprint) in HTML form
Pseudospectral Solutions to some Singular Nonlinear BVPs. Applications in nonlinear mechanics.
Abstract
We solve by Laguerre collocation method two genuinely nonlinear singularly perturbed boundary value problems formulated on the half-line. First, we are concerned with solutions to a model equation for low Reynolds number flow, the so-called Cohen, Fokas, Lagerstrom model. Then we compute monotonously increasing solutions, the so-called ”bubble type solutions”, to density profile equation for the description of the formation of microscopical bubbles in a nonhomogeneous fluid. We compare the results obtained in the latter case with those carried out by shooting or polynomial collocation both coupled with domain truncation.
The collocation based on Laguerre functions avoid the domain truncation, exactly impose any kind of boundary conditions at infinity and resolve with high accuracy the sharp interior or exterior layer of the solution. The method is fairly easy implementable, reliable and even more efficient in resolving the sharpest interior layer than previously mentioned methods. The accuracy of the method is also tested on the classical Blasius problem. We solve with the same method the eigenvalue problem obtained by linearization around the constant solution, which corresponds to the case of a homogeneous fluid (without bubbles), and observe that this solution is stable.
Keywords:
Singular nonlinear BVPs · Collocation · Laguerre functions · Semi-infinite domain · Blasius problem · Low Reynolds number flows · Density profile equation · Foundation engineering problem1 Introduction
A large variety of physical phenomena exhibit thin regions with fairly high variation of parameters which describe their behavior, the so called boundary layers. For instance, viscous flows have such layers next to solid surfaces where the tangential velocity increases rapidly from zero. The use of finite differences or of the more efficient Chebyshev collocation in conjunction with successive stretching is expensive when such phenomena are numerically analyzed. Thus one of the main aim of this study is to introduce a relatively low in cost method which improve considerably the resolution of the boundary layers.
From the mathematical point of view we are mainly concerned with the numerical treatment of some singular nonlinear second order boundary value problems attached to ordinary differential equations defined on the half-line. The linearization of such problems around some constant solutions are also considered.
The first challenge of such problems consist in imposing the boundary conditions at infinity. The most frequent remedy for this difficulty is the domain truncation or a sort of a change of coordinates (”mapping”). Up to our knowledge only for the classical Blasius problem there exists a rigorous error analysis related to the truncated boundary formulation of this problem. The result is due to Rubel LAR ( see also RF ). A general and at the same time rigorous discussion on this topic is available in the well known paper of Lentini and Keller LK . The main difficulty with their asymptotic boundary condition (ABC) method consists in the fact that this method, in the nonlinear case, produces nonlinear boundary conditions. Alternatively, the use of Laguerre functions, which means the Laguerre polynomials times , assures the exact fulfillment of boundary conditions at infinity.
A second genuine difficulty is the resolution of narrow regions of sharp variations of unknowns. Tang and Trummer in TT observe that very thin boundary layers must have at least one or two collocation points within boundary layer in order to assure reliable outcomes. But this results in extremely fine discretization if the relative spacing of the grid points remains unchanged. Thus they invoke a coordinate stretching technique in conjunction with Chebyshev collocation in order to solve linear second order singular perturbed BVPs. This is a frequently used manner to solve singular perturbation problems. In Laguerre collocation a scaling parameter, which maps the half-line in itself, will assure a suitable distribution of collocation nodes in regions of interest.
Consequently, in order to overcome these difficulties we use in this paper a Laguerre collocation method based on Laguerre functions. Systematic results in solving linear second order boundary value problems and respectively eigenvalue problems, both formulated on a semi-infinite interval, were first obtained by Weideman and Reddy in their seminal paper WR and then by Boyd et al. in JPB . Boyd et al. carries out a detailed comparison between Fourier-sine method, Laguerre series and rational Chebyshev expansion in solving the hydrogen atom problem (Coulomb-Schrödinger equation). They remark that pseudospectral methods based on Laguerre series and rational Chebyshev expansion are better suited for problems in the interval than Fourier method because they are less sensitive to the variation of the scaling parameter.
The paper is structured as follows. In Section 2, we shortly review the Laguerre collocation successfully used in our previous paper CIG and write down the general form of the nonlinear algebraic system in which this method cast a specific nonlinear singular boundary value problem formulated on the half-line. In Section 3, we reconsider the Blasius problem with respect to the error introduced by domain truncation. In Sections 4 and respectively 5, we introduce and solve two challenging test problems in physics (fluid mechanics and thermodynamics). The first one is a model equation for low Reynolds number flows due to Cohen, Fokas and Lagerstrom. It is of particular concern here because its solution is not a monotone one on the interval of interest (see Fig 1 and Fig 2 in Sect. 4). This lack of monotonicity is an important difference when compared with the Blasius problem or even the second test problem. This second test problem is the density profile equation from hydrodynamics. As we do not have a software control of the achieved accuracy, we choose to validate the obtained numerical results via a mesh refinement, i.e., by repeatedly increasing the cut off parameter in the Laguerre interpolating representation of the solution. Meaningful results are reported for illustrative purposes in Sections 4 and 5 for both problems. Moreover, in Subsection 5.1 we solve a singular Sturm-Liouville problem obtained by linearization around a constant solution. We find pseudospectrum of this problem as well as the first five eigenvectors and comment on the stability of this solution. Section 6 deals with conclusions supported by evidences of the present work.
2 A Laguerre collocation technique
We are interested in an accurate solution to the following singular nonlinear boundary value problem
| (1) |
where is a non negative integer, stands for a set of real parameters and is a continuous real map. The real parameters and in the boundary conditions do not vanish simultaneously.
Up to our knowledge a general theory for the existence (and uniqueness) of solutions to problems (1) is not available. Thus, in spite of the fact that we do not want to elaborate in detail on this topic, we observe that for some nonlinearity and boundary conditions the problem could be embedded in the following one
| (2) |
where and are assumed to be continuous. O’Regan in DOR has proved some existence results establishing first the solution existence on a finite interval and then extending the result by Arzela-Ascoli theorem on the semi-infinite interval.
In order to implement the Laguerre collocation for problem (1) we use the differentiation matrices from WR and implement boundary conditions making use of the procedure of removing technique of independent boundary conditions introduced by Hoepffner in JH . This strategy was successfully used in our previous paper CIG and is detailed there.
Thus we cast (1) into the nonlinear algebraic system
| (3) |
where the vector contains the nodes which are the roots of the Laguerre polynomial of order , indexed in increasing order of magnitude. It is well known that as These nodes are kept and the first node is removed. We remove only one node because only one of the parameters and do not vanish in the problems which follow. The interval can be mapped to itself by change of variables , where is any positive real number (the scaling factor). Laguerre method therefore contains a free-parameter which will play a key role in our analysis.
The vector contains the unknown values of in the nodes and are the first and the second order differentiation matrices with boundary conditions enforced. As we use MATLAB codes and symbols, stands for the diagonal matrix with Throughout this paper the nonlinear were solved by MATLAB built in function fsolve. The initial guess was chosen in each and every case in order to mimic the correct solution and we have obtained convergent procedures.
The problems of type (1) are particularly difficult because of the singularity in the coefficient of the first order differentiation term. To cope with this difficulty we varied the scaling factor such that a fine enough grid will resolve the solution around singularity.
3 The Blasius problem revisited
When the independent variable is denoted by and the dependent one by this problem reads
| (4) |
In the truncated boundary approach strategy, the boundary condition at infinity is replaced by the same condition at a given finite value . Thus we define as the solution of
| (5) |
The error related to is defined by
| (6) |
Rubel in LAR found out the following upper bound for this error:
| (7) |
It means that Laguerre collocation method used to solve this problem in our paper CIG has produced errors of order (see also Fig. 4 in this paper). Roughly approaches unity as and thus the r. h. s. in (7) depends essentially on the drag at large distances away from fixed boundary.
We have to remark that in the actual computed value of , and its first two derivatives in , the truncation and round off errors of the collocation are also incorporated. However, as we were not aware of the estimation (7) at the time the paper CIG was edited, this discussion validate once more the Laguerre collocation results.
4 A model equation for low Reynolds number flows (Cohen, Fokas, Lagerstrom)
The following problem was introduced by one of the authors of CFL , namely Lagerstrom (1961)
| (8) |
The differential equation in (8) is the equation for the time independent temperature distribution in an infinite medium. Generally, it is somewhat an unrealistic physical model where is a radial coordinate in -dimensional space and is the temperature. The first two terms come from Laplace’s operator, the last two represent nonlinear autonomous heat sources unfortunately not validated in any actual physical model. The temperature equals zero on the sphere and equals at large distances. The intuitive reasoning indicated that for one-dimensional case the problem is not singular. This was verified by the construction of an exact solution in this case (by quadrature and inversion of a function). If and one may make their values unity (even simultaneously) by a scale transformation in and . However, because is an interesting case and occurs in an auxiliary equation, i.e., Stokes equation, we consider arbitrary nonnegative values for and . For , (8) has a unique solution. Our numerical approximation for such a solution when and is depicted in Fig. 1.
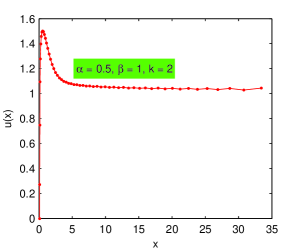
Singular asymptotic techniques may and have been used only if . For the problem may be solved explicitly. The boundary value problem then has a solution which is unique only if Thus is an important limiting case.
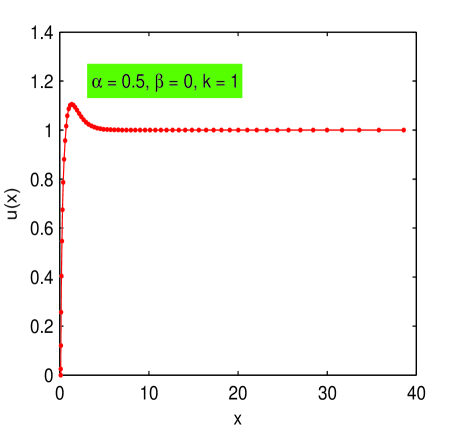
Hsiao in H gave a rigorous discussion of the existence of a solution to (8) for and Such a solution is depicted in Fig. 2 for the same value of and as stated above. The case has the advantage of being applicable to ”real” problems, i.e., to some problems in fluid dynamics for which (8) is a model.
Both curves depicted in Fig. 1 and Fig. 2 behaves in perfect accordance with the asymptotic for predicted by Markowich in PAM . There is still a difference between them for large . It seems that the nonlinearity affects to some extent the stability of numerical process but ill conditioning of the differentiation matrices does not appear to be a serious problem as our experiments indicate.
5 A singular boundary value problem in hydrodynamics-the density profile equation
We investigate the monotonously increasing solutions of the problem
| (9) |
where stands for the density of a fluid, and for the sake of simplicity we can choose the following values of the parameters: without restriction of generality, which corresponds to a physically meaningful case and varying in the range such as to reflect different physical situations. The above equation is called the density profile equation and has the origins in the Cahn-Hillard theory which is used in hydrodynamics to study the behavior of non-homogeneous fluids. In their paper KKLW , Kitzhofer, Koch, Lima and Weinmūller find by polynomial collocation the so called ”bubble-type solution”. When such solution exists it has exactly one zero in and is interpreted as the bubble radius. They also satisfy and The derivative of the solution attains a maximum at some value and tends to at infinity. Eventually, a bubble-type solution exhibits an interior layer which becomes sharper as We also have to observe that the problem (9) always admits the constant solution which physically corresponds to the case of a homogeneous fluid, i.e., without bubbles.
In KKLW the authors transform the problem to a finite interval and show that essential singular problem obtained is well-posed. In contrast we solve (9) by Laguerre collocation introduced in the previous sections. In fact, with respect to singularly perturbed problems, in TT , Tang and Trummer observe that ”for good resolution of the numerical solution at least one of the collocation points ought to lie in the boundary layer”. Thus, for and scaling factor we get the repartition of the Laguerre collocation points plotted in Fig. 3. For the singular problem at hand it seems fairly well suited.
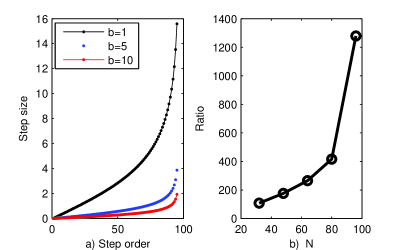
The ration between the largest step size and the smallest (the closest to ) equals With such a density of collocation nodes we obtained first the solution of (9) for It is depicted in Fig. 4.

For the solutions to the same problem are displayed in Fig. 5. The values of unknown function in the radius and elapsed CPU time when the nonlinear algebraic system involved by Laguerre collocation is solved by MATLAB code fsolve are reported in Tab. 1. All computations were carried out using 2010a variant of MATLAB on an HPxw8400 workstation with clock speed of 3.2Ghz.
| . | |||
|---|---|---|---|
Thus, unlike the paper KKLW we solve the problem (9) for extreme values of , i.e., and The solutions displayed in Fig. 5 reproduce correctly the similar solutions from KKLW . The computed values of and from Tab. 1 are fairly closed to the corresponding values displayed in the above quoted paper. It is also worth nothing that the computational effort increase with parameter as is apparent from the last column of Tab. 1. The same difficulty is reported in KKLW . Moreover, for and even the continuation could hinder fsolve to find a converging solution. Thus, a particular special attention must be payed for the initial guess in these cases. It is also clear from the last two lines of Tab. 1 that rounding off errors contaminate the solution for large
As a final word we have to remark that our numerical experiments carried out with respect to the problem (9) and based on mapping coupled with Chebyshev collocation provided totally unsatisfactory results.
5.1 Linearization of problem (9)
In order to get more insight into the challenging problem (9) we will analyze its linearization around the constant solution It reads
| (10) |
The Laguerre collocation casts this problem into the generalized eigenvalue problem
| (11) |
where the matrices and are defined as
the vector contains the nodes and the matrices are defined in Section 2. The pseudospectrum of this problem when is provided in Fig. 6.

It shows a high degree of non normality of this problem. This statement is backed by the so called Henrici number. We recall that for a square matrix this number is defined by
where stands for the Frobenius (euclidian) norm of a matrix and the symbol denotes the conjugate transpose (see Henrici H , Chaitin-Chatelin and Fraisse ChF or our contribution CIG2 ). Actually ranges between and . Thus the Henrici number of order computed for suggests that the matrix pencil is far from a normal one.
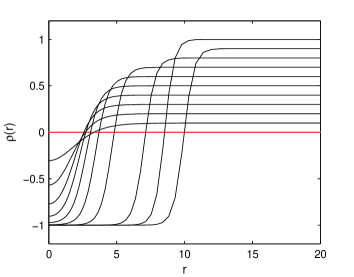
The eigenvalues are real and negative. The rightmost one was found to be which implies the stability of constant solution. The first five eigenvectors are available in Fig. 7.
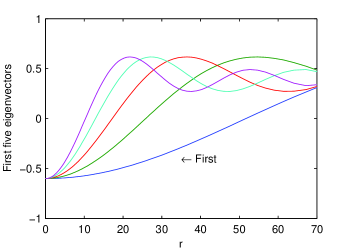
All of them satisfy the boundary condition in the origin, are monotonously increasing for and converge to the solution for large .
Throughout this paper we have applied the eight Rule-of-Thumb formulated by Boyd in his monograph JPBoyd . Thus in order to test the reliability of our numerical results we repeated our numerical experiments with different and have compared the results. Actually we have considered in the range .
6 Concluding remarks
All in all, the Laguerre collocation has incorporated without any difficulty and avoiding domain truncation the boundary conditions at infinity.
It is largely accepted that in order to obtain a fine resolution for fairly sharp layer problems, at least some of the grid points should lie in the boundary layer no matter how narrow the boundary layer is. In the Laguerre collocation method used above this desiderate is accomplished by making use of the scaling parameter . Its tuning is carried out manually in a reduced number of numerical experiments. However, this could be considered as a drawback of our strategy when compared with the automatic mesh adaptation for sharp layers proposed in KKLW . Fortunately, we have reported results for sharpest layer which were not previously obtained. We also believe that numerical solutions for Cohen, Fokas and Lagerstrom type equation are for the first time reported in this paper.
Anyway, an automatic generation of a suitable scaling parameter, for a specific problem, remains an open issue.
References
- (1) Boyd, J.P.: Chebyshev and Fourier Spectral Methods. Second Ed., Dover Publications, New York(2000)
- (2) Boyd, J.P., Rangan, C., Bucksbaum, P.H.: Pseudospectral methods on semi-infinite interval with application to the hydrogen atom; a comparison of mapped Fourier sinc method with Laguerre series and rational Chebyshev expansion. J. Comput. Phys. 188,56-74(2003)
- (3) Chaitin-Chatelin, F., Fraisse, V.: Lectures on Finite Precision Computation. SIAM Philadelphia(1996)
- (4) Cohen, D.S., Fokas, A., Lagerstrom P.A.: Proof of some Asymptotic Results for a Model Equation for low Reynolds Number Flow. SIAM J. Appl. Math. 35,187-207(1978)
- (5) Fazio, R.: A Free Boundary Value Approach and Keller’s Box Scheme for BVPs on Infinite Intervals. J. Comput. Appl. Math. 140,331-344(2002)
- (6) Gheorghiu, C.I.: On the Spectral Characterization of some Chebyshev Type Methods; Dimension vs. Structure. Studia Univ. ”Babes-Bolyai” L, 61-66(2005)
- (7) Gheorghiu, C.I.: Spectral Methods for Differential Problems. Casa Cartii de Stiinta Publishing House, Cluj-Napoca(2007)
- (8) Gheorghiu, C.I., Rommes, J.: Application of the Jacobi-Davidson method to accurate analysis of singular linear hydrodynamic stability problems. Int. J. Numer. Meth. Fl. (2012) http://dx.doi.org/10.1002/fld.3669
- (9) Gheorghiu, C.I.,: Laguerre collocation solutions to boundary layer type problems. Numer. Algorithms (2012) http://dx.doi.org/DOI: 10.1007/s11075-012-9670-y
- (10) Henrici, P.: Bounds for iterates, inverses, spectral variation and fields of values of non-normal matrices. Numer. Math. 4, 24-40(1962)
- (11) Hoepffner, J.: Implementation of boundary conditions. http://www.lmm.jussieu.fr/hoepffner/research/realizing.pdf(2010). Accessed 25 August 2011
- (12) Hsiao, G.C.: Singular perturbations for a nonlinear differential equation with a small parameter. SIAM J. Math. Anal. 4,283-301(1973)
- (13) Kitzhofer, G., Koch, O., Lima, P., Weinm ller, E.: Efficient Numerical Solution of the Density Profile Equation in Hydrodynamics. J. Sci. Comput. 32, 411-424(2007)
- (14) Lentini, M., Keller, H.B.: Boundary Value Problems on Semi-Infinite Intervals and their Numerical Solution. SIAM J. Numer. Anal. 17,577-604(1980)
- (15) O’Regan, D.: Solvability of Some Singular Boundary Value Problems on the Semi-Infinite Interval. Canadian J. Math. 48,143-158(1996)
- (16) Markowich, P.A.: Analysis of Boundary Value Problems on Infinite Intervals. SIAM J. Math. Anal. 14,11-37(1983)
- (17) Pruess, S., Fulton, C.T., Mathematical Software for Sturm-Liouville Problems. ACM T. Math. Software 19,360-376(1993)
- (18) Rubel, L.A.: An estimation of the error due to the truncated boundary in the numerical solution of the Blasius equation. Q. Appl. Math. 13,203-206(1955)
- (19) Tang, T., Trummer, M.R.: Boundary Layer Resolving Pseudospectral Methods for Singular Perturbation Problem, SIAM J. Sci. Comput. 17,430-438(1996)
- (20) Trefethen, L.N.: Computation of pseudospectra. Acta Numer. 8,247-295(1999)
- (21) Weideman, J.A.C., Reddy, S.C.: A MATLAB Differentiation Matrix Suite, ACM T. Math. Software 26, 465-519(2000)
1. Boyd, J.P.: Chebyshev and fourier spectral methods, 2nd edn. Dover Publications, New York (2000)
2. Boyd, J.P., Rangan, C., Bucksbaum, P.H.: Pseudospectral methods on semi-infinite interval with application to the hydrogen atom; a comparison of mapped Fourier sinc method with Laguerre series and rational Chebyshev expansion. J. Comput. Phys. 188, 56–74 (2003)
3. Chaitin-Chatelin, F., Fraisse, V.: Lectures on finite precision computation. SIAM, Philadelphia (1996)
4. Cohen, D.S., Fokas, A., Lagerstrom, P.A.: Proof of some asymptotic results for a model equation for low Reynolds number flow. SIAM J. Appl. Math. 35, 187–207 (1978)
5. Fazio, R.: A survey on free boundary identification of the truncated boundary in numerical BVPs on infinite intervals. J. Comput. Appl. Math. 140, 331–344 (2002)
6. Fazio, R.: A free boundary value approach and Keller’s box scheme for BVPs on infinite intervals. Int. J. Comput. Math. 80, 1549–1560 (2003)
7. Gheorghiu, C.I.: On the spectral characterization of some Chebyshev type methods; dimension vs. structure. Studia Univ. “Babes-Bolyai” L, 61–66 (2005)
8. Gheorghiu, C.I.: Spectral methods for differential problems. Casa Cartii de Stiinta Publishing House, Cluj-Napoca (2007)
9. Gheorghiu, C.I., Rommes, J.: Application of the Jacobi-Davidson method to accurate analysis of singular linear hydrodynamic stability problems. Int. J. Numer. Meth. Fl. 71, 358–369 (2012)
10. Gheorghiu, C.I.: Laguerre collocation solutions to boundary layer type problems. Numer. Algor. 64, 358–401 (2012)
11. Henrici, P.: Bounds for iterates, inverses, spectral variation and fields of values of non-normal matrices. Numer. Math. 4, 24–40 (1962)
12. Hsiao, G.C.: Singular perturbations for a nonlinear differential equation with a small parameter. SIAM J. Math. Anal. 4, 283–301 (1973)
13. Kitzhofer, G., Koch, O., Lima, P.M., Weinmuller, E.: Efficient numerical solution of the density ̈ profile equation in hydrodynamics. J. Sci. Comput. 32, 411–424 (2007)
14. Konyukhova, N.B., Lima, P.M., Morgado, M.L., Soloviev, M.B.: Bubbles and droplets in nonlinear physics models: analysis and numerical simulation of singular nonlinear boundary value problems Comput. Math. Math. Phys. 48, 2018–2058 (2008)
15. Kulikov, G.Y., Lima, P.M., Morgado, M.L.: Analysis and numerical approximation of singular boundary value problems with p-Laplacians in fluid mechanics. J. Comput. Appl. Math. doi:10.1016/j.cam.2013.09.071
16. Lentini, M., Keller, H.B.: Boundary value problems on semi-infinite intervals and their numerical solution. SIAM J. Numer. Anal. 17, 577–604 (1980)
17. Lima, P.M., Konyukhova, N.B., Chemetov, N.V., Sukov, A.I.: Analytical- numerical investigation of bubble-type solutions of nonlinear singular problems. J. Comput. Appl. Math. 189, 260–273 (2006)
18. O’Regan, D.: Solvability of some singular boundary value problems on the semi-infinite interval. Can. J. Math. 48, 143–158 (1996)
19. Markowich, P.A.: Analysis of boundary value problems on infinite intervals. SIAM J. Math. Anal. 14, 11–37 (1983)
20. Pruess, S., Fulton, C.T.: Mathematical software for Sturm-Liouville problems. ACM T. Math. Softw. 19, 360–376 (1993)
21. Rubel, L.A.: An estimation of the error due to the truncated boundary in the numerical solution of the Blasius equation. Q. Appl. Math. 13, 203–206 (1955)
22. Tang, T., Trummer, M.R.: Boundary layer resolving pseudospectral methods for singular perturbation problem. SIAM J. Sci. Comput. 17, 430–438 (1996)
23. Trefethen, L.N.: Computation of pseudospectra. Acta Numer. 8, 247–295 (1999)
24. Weideman, J.A.C., Reddy, S.C.: A MATLAB differentiation matrix suite. ACM T. Math. Softw. 26, 465–519 (2000)
