Abstract
Our main aim is the accurate computation of a large number of specified eigenvalues and eigenvectors of Mathieu’s system as a multiparameter eigenvalue problem (MEP). The reduced wave equation, for small deflections, is solved directly without approximations introduced by the classical Mathieu functions. We show how for moderate values of the cut-off collocation parameter the QR algorithm and the Arnoldi method may be applied successfully, while for larger values the Jacobi–Davidson method is the method of choice with respect to convergence, accuracy and memory usage.
Authors
Călin-Ioan Gheorghiu
(Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy)
M. E. Hochstenbach
(Department of Mathematics and Computer Science, TU Eindhoven)
B. Plestenjak
(Department of Mathematics, University of Ljubljana)
J. Rommes
(NXP Semiconductors, The Netherlands)
Keywords
References
See the expanding block below.
Cite this papaer as
C.I. Gheorghiu, M.E. Hochstenbach, B. Plestenjak, J. Rommes, Spectral collocation solutions to multiparameter Mathieu’s system, Appl. Math. Comput., 218 (2012) 11990-12000.
doi: 10.1016/j.amc.2012.05.068
About this paper
Print ISSN
0096-3003
Online ISSN
Google Scholar Profile
google scholar link
Paper (preprint) in HTML form
Spectral collocation solutions to multiparameter Mathieu’s system
Abstract
Our main aim is the accurate computation of a large number of specified eigenvalues and eigenvectors of Mathieu’s system as a multiparameter eigenvalue problem (MEP). The reduced wave equation, for small deflections, is solved directly without approximations introduced by classical Mathieu functions. We show how for moderate values of the cut-off collocation parameter the QZ algorithm and the Arnoldi method may be applied successfully, while for larger values the Jacobi-Davidson method is the method of choice with respect to convergence, accuracy and memory usage.
Key words: Mathieu’s system; Chebyshev collocation; multiparameter eigenvalue problems; Jacobi–Davidson; tensor Rayleigh quotient iteration.
1 Introduction
Mathieu’s system is often used in the literature as a motivating example for the introduction of multiparameter eigenvalue problems, see, for example, [25]. This MEP approach of this well known system is the most natural one. The system is obtained if separation of variables is applied to solve the vibration of a fixed elliptic membrane. However, to the best of our knowledge, the accurate numerical solution of Mathieu’s system as a two-parameter eigenvalue problem was never studied in detail. Ruby in his paper [20] provides some examples from science and technology arguing that they deserve accurate solutions of Mathieu’s system. From the paper of Igbokoyi and Tiab [15], as well as from other papers quoted there, it is apparent that the case of an ellipse with the minor axis approaching zero is of tremendous importance in petroleum engineering.
The main aim of this paper is to find a large number (more than four hundred) of even and odd, and , eigenfrequencies and eigenmodes of Mathieu’s system as a MEP very accurately. Neither the radial Mathieu’s equation nor the Mathieu’s system, as a two-parameter eigenvalue problem, have been solved using Chebyshev collocation (pseudospectral) method. This approach, in conjunction with various methods to solve the (discretized) algebraic MEP, is considered in this paper. For these methods, as well as for the normality of the discretization matrices, is paid a particular attention. Thus, for small to moderate values of the cut-off collocation parameter, , the QZ algorithm and shift-and-invert Arnoldi method work satisfactory. For larger they fail. The remedy is a Jacobi-Davidson based method which accurately and efficiently solves these cases.
In fact the literature concerning the numerics of the second problem is rather poor. The paper of Neves [16] contains some numerical results along with a Klein oscillation theorem for the multiparameter Mathieu’s system. These numerical results came from an ad hoc method. It involves a shooting scheme based on Runge-Kutta method used to solve a two-point boundary value problem. Troesch and Troesch find in their paper [24] two lowest eigenvalues using for the representation of the Mathieu’s functions the Bessel functions. Gutiï¿rrez-Vega et. al. in their paper [9] use the Fourier representation in order to find classical Mathieu’s functions. Without the need of special functions, Wilson and Scharstein [28] use a Fourier collocation method to find a ”wide range” of eigenfrequencies, i.e., first one hundred modes. They do not solve a MEP. Instead they solve a sequence of two generalized eigenvalues and this seems to affects the accuracy of their solutions.
In contrast, the angular Mathieu’s equation is solved by Trefethen in [23] and Weideman and Reddy in [26] by Fourier collocation and thoroughly analyzed by Boyd in his monograph [2]. More recently, Shen and Wang [21] provide approximation results (in Sobolev spaces) for the eigenmodes of the first Mathieu equation. They also solve the second Mathieu equation by a spectral Galerkin method and eventually by a Legendre spectral-Galerkin method they solve a Helmholtz and a modified Helmholtz equation.
The paper is organized as follows. In Sect. 2 we introduce the Mathieu system as a MEP, i.e., the four possible differential MEPs. We comment on the two-parameter algebraic eigenvalue problems in Sect. 3 and provide an overview of the Jacobi-Davidson method to solve such problems in Sect. 4. The Chebyshev collocation discretization as well as a finite difference discretization of the Mathieu’s system as a MEP is considered in Sect. 5. Our numerical results are presented in Sect. 6. Sect. 7 concludes.
2 Mathieu’s system
The coupled system of Mathieu’s angular and radial equations in which and are independent parameters will be thought of now as a multiparameter (two parameter) eigenvalue problem. The following four MEPs can be formulated with respect to Mathieu’s system:
-
•
a -even problem
(1) -
•
a -even problem
(2) -
•
a -odd problem
(3) -
•
a -odd problem
(4) These coupled systems of two-point boundary value problems come from the problem of a vibrating elliptic membrane with fixed boundaries ,
(5) when the separation of the variable, i.e., is used in the elliptical coordinates and
(6) Thus
where is half the distance between the foci of the membrane. The parameter is related to the eigenfrequency by
and is the parameter arising in the separation of variables. Volkmer analyses in details in his monograph [25] the above four systems. For these right definite MEP, he provides results concerning the existence and countability of eigenvalues, numbers of zeros of eigenfunctions and the completeness of even and odd sets of eigenmodes. His analytical results are exhaustive. A Klein oscillation theorem is also available in [16] and some other useful comments on the formulations above can be found in [4]. The Mathieu system can also be ”embedded” in the most general setting of the multiparameter eigenvalue problem for ordinary differential equations formulated by Sleeman in [22].
3 Algebraic two-parameter eigenvalue problem
An algebraic two-parameter eigenvalue problem has the form
| (7) |
where , and are given complex matrices, , , and . A pair is called an eigenvalue if it satisfies (7) for nonzero vectors and . The tensor product is then the corresponding eigenvector.
The two-parameter eigenvalue problem (7) can be expressed as two coupled generalized eigenvalue problems as follows. On the tensor product space of the dimension we define so called operator determinants
(for details on the tensor product and relation to the multiparameter eigenvalue problem, see, for example, [1]). The two-parameter eigenvalue problem is nonsingular when is nonsingular. In this case the matrices and commute and (7) is equivalent to a coupled pair of generalized eigenvalue problems
| (8) |
for decomposable tensors , (see [1]).
There exist some numerical methods for two-parameter eigenvalue problems. If is small, we can apply the existing numerical methods for the generalized eigenvalue problem to solve the coupled pair (8). An algorithm of this kind, which is based on the QZ algorithm, is presented in [12].
When is large, it is not feasible to compute all eigenpairs. There are some iterative methods that can be applied to compute some solutions. Most of them require good initial approximations in order to avoid misconvergence. One such method, that we apply in our numerical experiments, is the Tensor Rayleigh Quotient Iteration (TRQI) from [17], which is a generalization of the standard Rayleigh quotient iteration, (see, e.g., [6]). This method computes one eigenpair at a time.
In case when we are interested in more than just one eigenpair and we do not have any initial approximations, a method of choice is a Jacobi–Davidson type method [12]. The state-of-the-art, which uses harmonic Ritz values [13], can be used to compute a small number of eigenvalues of (7), which are closest to a given target . The method is presented in the next section.
4 Overview of Jacobi–Davidson method
For the numerical solution we exploit a Jacobi–Davidson method as developed in [12, 13, 19]. We will now present a brief overview.
In this method the eigenvectors and are sought in search spaces and , respectively. There are two main phases: expansion of the subspaces, and extraction of an approximate eigenpair from the search space. First consider the subspace expansion. Suppose that we have approximate eigenvectors and with corresponding approximate eigenvalue ; for instance, the tensor Rayleigh quotient. We are interested in orthogonal improvements and such that
| (9) | |||||
| (10) |
Let
be the residuals of vector and value . We can rewrite (LABEL:problem2aa) and (9) as
We neglect the second-order correction terms and . Let be a matrix with columns (for reasons of stability, preferably orthonormal) such that
and let be
With the oblique projection
onto along , it follows that
| (13) |
Therefore, we can project out the first-order terms and using this oblique projection, reformulating (4) and (4) (without the neglected second-order correction terms) as
| (14) |
for and . We use (possibly) inexact solutions and to this linear system to expand the search spaces and .
Now we focus on the subspace extraction. As introduced in [13], the harmonic Rayleigh–Ritz extraction for the MEP extracts approximate vectors , and corresponding values and by imposing the Galerkin conditions
| (15) |
This generally turns out to be a method of choice for interior eigenvalues near a target . A very basic pseudocode for the method is given in the following algorithm, where RGS stands for repeated Gram–Schmidt, or any other numerically robust method to expand an orthonormal basis.
5 Discretization of Mathieu’s system as a MEP
Our previous numerical experiments concerning non-standard, high order and singularly perturbed eigenvalue problems reported in [3, 7, 8] proved that Chebyshev collocation method is fairly accurate, flexible and implementable. It turned out to be superior to the spectral Galerkin or tau method also based on Chebyshev polynomials. The well known monograph of Fornberg [5] provides a thorough analysis with how, when and why this pseudospectral approach works.
Thus, the Chebyshev collocation discretization of MEP (1) reads
| (16) |
where and are second order differentiation matrices in the Chebyshev nodes of the second kind , i.e.,
In the symbol the upper indices and stand for even and period, and the lower index for the Neumann boundary conditions
which are enforced. Similarly, in the mixed boundary conditions
are introduced, so comes from the first and from the second boundary condition. We used the seminal paper of Weideman and Reddy [26] to obtain the entries of these two matrices and the simple and general strategy of Hoepffner [14] to impose all boundary conditions. These matrices are also available in the book of Trefethen [23]. The vectors and contain the unknown values of and in the nodes .
Thus, the problem (16) is an algebraic MEP of type (7) with standing for . The discretizations for the last three problems (2), (3) and (4) are analogous.
Unfortunately, the matrices and are dense, non-symmetric and have high condition numbers (see for instance [8]).
The pseudospectra (see [11] for definition and numerical code) of even problems (1) and (2) are depicted in Fig. 1. This picture shows two mildly non-normal MEP with decreasing non-normality for large .
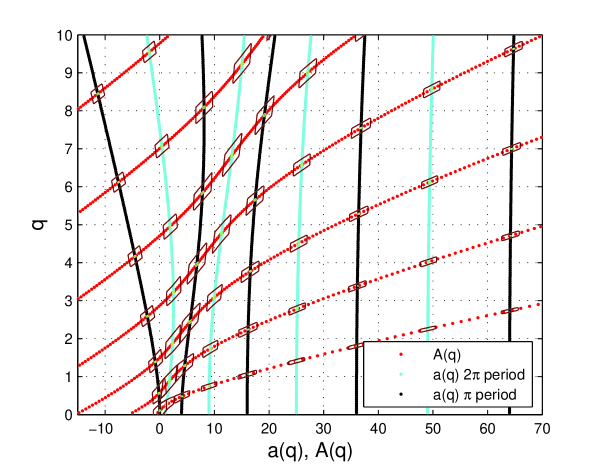
It is worth noting at this moment that the curves represent the solutions of the first Sturm-Liouville problems in (1) and (2) for They are the interlaced quasi ”vertical” curves in Fig. 1. The family of curves depicts the solutions of the second Sturm-Liouville problem in (1) or (2) for the same range of . They are represented by the quasi ”oblique” curves. Their intersections localize the eigenpairs of MEP (1). Our Fig. 1 refines Fig. 1 from the paper of Neves [16].
The Chebyshev collocation discretization of MEP (4) reads
| (17) |
In the upper index stands for odd property, the index for period and for the mixed boundary conditions
. The matrix with the lower index involves the symmetric Dirichlet boundary conditions
The pseudospectra of odd problems (3) and (4) are depicted in Fig. 2.
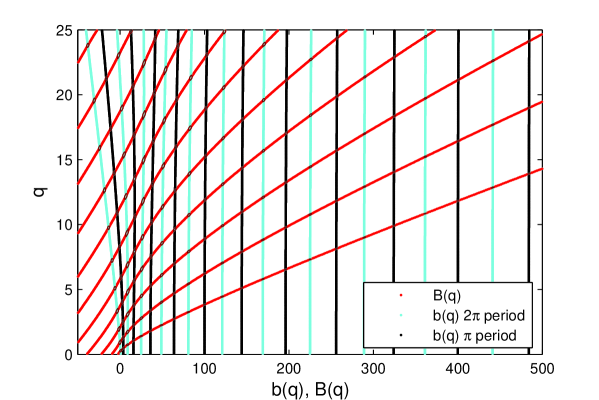
It shows, two even more normal problem than (1) and (2). The explanation consists in the fact that the Dirichlet boundary conditions
in (3) and (4) induce a sort of symmetry in the differentiation matrices, i.e. the matrix is more normal than .
In order to evaluate the performances of our strategy we carried out numerical experiments on the finite difference discretization of our differential eigenvalue problems. Thus the usual finite difference of (1) reads
| (18) |
where and stand for the second order centered finite difference approximation of the second derivative in the equispaced nodes .
The matrices and are now symmetric and tridiagonal of order and respectively and the Neumann boundary conditions were introduced by mirror imaging technique described in the monograph of Quarteroni et. al. [18], p. 549. Despite these simplifications in (18) the numerical results provided in the next section are obviously inferior to those obtained by Chebyshev collocation (see Tab. 3 and Tab. 4).
It is important to point out at this moment that in their paper [28] Wilson and Scharstein use a Fourier collocation method (and not Galerkin!) in order to discretize the Mathieu’s system. Their shape (trial) functions are some trigonometric functions which implicitly satisfy the boundary conditions but it is not clear from this paper what is the distribution of their nodes and how they are clustered to the boundary. As this paper is detailed in the monograph [29] it seems that they use a uniform grid. Our strategy takes the advantage of the Chebyshev clustering to the boundary.
6 Numerical examples
In our numerical experiments we compute solutions of Mathieu’s systems (1)–(4) using discretizations from Sect. 5. For each of the four systems we know from Volkmer [25] that for every pair of nonnegative indices there exists a pair with nonzero functions and such that has exactly zeros on and has exactly zeros on . This is one way how we can index the solutions.
Another option of indexing comes from the fact that Mathieu’s systems (1)–(4) are related to the problem of a vibrating elliptic membrane with fixed boundaries (5). Each solution gives an eigemode of (5) with the eigenfrequency . The solutions of (1) and (2) give all even eigenmodes of (5). We order the even eigenmodes so that To each even eigenmode (see, for example, [16] or [28]) we can associate an index , where is the number of zeros of on , and is the number of zeros of on . The eigenmode is then In a similar way the solutions of (3) and (4) give the odd eigenmodes of (5).
The choice of the method to solve the algebraic MEP’s depends on the requested eigenvalue and the required accuracy. It is clear that if we want to compute a higher eigenfrequency very accurately, we need a larger . Depending on the size of , we propose to use one of the following methods:
-
a)
EIG-: When is small, we can apply the existing numerical methods (for instance eig in Matlab) to the eigenvalue problem
(19) where the matrix is of size . The obtained eigenvector is decomposable, i.e., , and it is easy to compute and from .
-
b)
EIGS-: When matrix is too large for a), we can apply the implicit shift-and-invert Arnoldi (available as function eigs in Matlab) on (19). One can see that the matrix is quite sparse. It has full blocks of size on its diagonal, whereas all non-diagonal blocks are diagonal matrices. In many cases, when we need just a small number of eigenvalues, b) is more efficient than a) even for small .
If is very large, this approach is not feasible anymore. The first problem is that the and factors of the LU decomposition of the matrix are virtually full triangular matrices, and we run out of memory.
Although we could try to use another solver instead of the default LU decomposition in eigs, there is another problem when is large. Namely, as the matrix has size , the method builds its search space by vectors of size , which is time and memory consuming.
-
c)
JD-: When is too large for b), we can apply the Jacobi–Davidson method. An advantage of the Jacobi–Davidson method is that it works with matrices and vectors of size . Therefore, the method might be applied when b) is too expensive.
The results were obtained using Matlab 2010b running on Intel Core Duo P8700 2.53GHz processor using 4GB of memory. In this environment, the approach EIGS- works up to , for larger we have to use JD-. The method EIGS- might be more efficient than EIG- if many eigenvalues are required.
Example 1
We compare EigElip, which is a Matlab implementation of our method EIGS-, to the Matlab function runelip by Wilson [27], which was used to compute the eigenfrequencies in [28].
The results in Table 1 show the results, obtained for the computation of the lowest even eigenfrequencies for the ellipse with given and . Parameters and for EigElip specify the number of points used for the discretization of Mathieu’s systems, which might be different for each of the two equations. The number is used for the angular equation and is used for the radial equation. The values are chosen so that the computed eigenfrequencies are correct to at least 8 decimal places. The parameter nrts in runelip specifies that the method computes all eigenfrequencies of index where and . The values are minimal possible so that all of the lowest eigenfrequencies are among the computed ones. The computational times, which are given in seconds, show that the new method is considerably faster than runelip. The values in the last column present the maximum absolute error of the computed eigenvalues. One can see that runelip is not accurate for higher eigenfrequencies.
| EigElip | runelip | |||||||
|---|---|---|---|---|---|---|---|---|
| time | error | nrts | time | error | ||||
| 2.2 | 5e-10 | (27,6) | 14.8 | 5e-10 | ||||
| 6.5 | 5e-9 | (39,9) | 34.9 | 5e-9 | ||||
| 17.2 | 1e-8 | (48,11) | 52.7 | 1e-8 | ||||
| 3.4 | 3e-10 | (27,6) | 18.2 | 3e-10 | ||||
| 11.3 | 5e-9 | (39,9) | 31.1 | 5e-9 | ||||
| 19.7 | 3e-3 | (39,9) | 51.9 | 3e-3 | ||||
| 3.2 | 3e-3 | (48,3) | 14.9 | 1e-9 | ||||
| 2.6 | 3e-3 | (24,9) | 13.4 | 1e-9 | ||||
Example 2
In this example we use Jacobi–Davidson with harmonic Ritz values, presented in Section 4, to compute eigenvalues close to a given target. Depending on the region of interest we do this for several targets. The results of this phase is a set of eigenpairs for . For each obtained eigenvalue we compute its index , where and are the number of zeros of and , respectively. Here we assume that vectors and are discrete approximations of continuous curves.
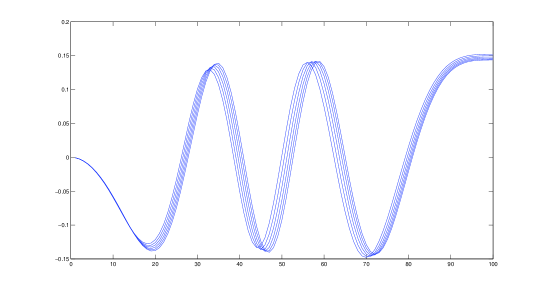
In the second phase we extend the obtained set by the TRQI. We exploit the following property of eigenvectors of Mathieu’s system. Let and be approximate eigenvectors belonging to eigenvalues with indices and , respectively. If and is close to , then and do not differ much. The same applies to and when and is close to . This is displayed on Fig. 3, where the part of the eigenvector corresponding to the eigenvalue with index for are presented. So, for each pair of eigenvectors, such that is close to and is close to , we can apply TRQI with an initial approximation in order to compute the eigenpair with the index . This simple approach usually converges in a couple of steps.
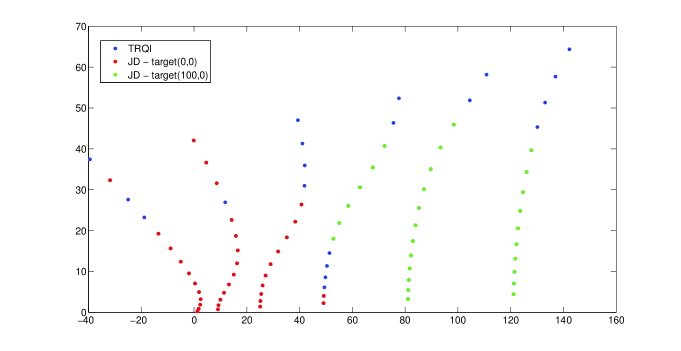
We take Chebyshev discretization (16) with matrices of size and two targets: and . For each target we do 200 outer iterations of the Jacobi–Davidson method with harmonic Ritz values. As preconditioners we take for , where is the current target. We apply 20 steps of GMRES to solve the correction equations. As a result, we get 36 eigenpairs for the target and 28 eigenpairs for the target . From these eigenpairs we compute additional 20 eigenvalues with the TRQI, so that in the end we have approximations for all eigenpairs of (1) with indices , such that and .
The computed eigenvalues are presented on Fig. 4 in three different colors. The red and the green eigenvalues were computed using the Jacobi–Davidson method with targets and , respectively, while the blue eigenvalues were computed using the TRQI. One can see that in a large majority the eigenvalues computed by the Jacobi–Davidson method are indeed the closest ones to the given target.
Example 3
Using the method EIGS- we can accurately compute higher eigenmodes than the previously reported in the literature.
For example we take and and compute the lowest 300 even eigenmodes using EigElip with and . The eigenmodes and for the eigenfrequencies and are presented in Figures 5 and 6, respectively.
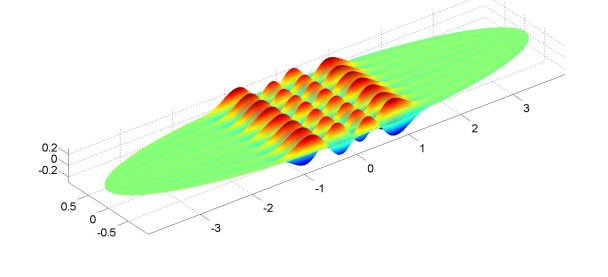
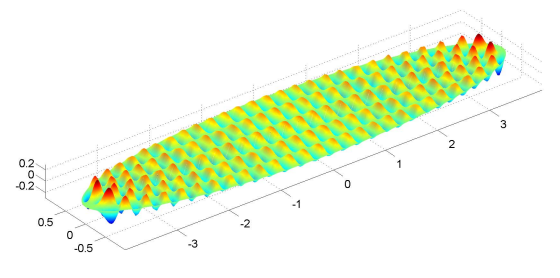
It is important to underline that higher eigenmodes, which require larger matrices, could not be obtained by EIG and EIGS methods due to memory limitations, while JS- was able to compute these eigenmodes up to the required accuracy.
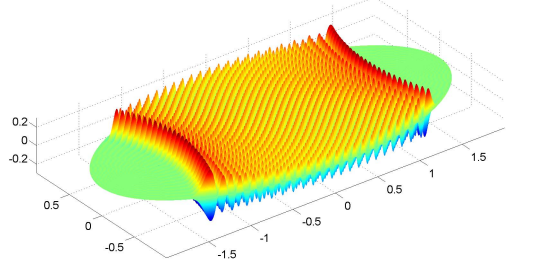
Using and the target we computed the even eigenfrequency of the ellipse with and that is closest to the target . The result is . Its eigenmode is presented on Fig. 7.
Example 4
There are certain applications that require the eigenmodes of an ellipse with a very large ratio . See, for instance, [15].
In this example we show that such problems can also be solved efficiently via the MEP approach. If we take the ellipse with and , and set and , then EigElip returns the 10 lowest even eigenfrequencies in Table 2. The 6th lowest even eigenmode is shown in Fig. 8.
| eigenfrequency | eigenfrequency | ||
|---|---|---|---|
| 1 | 1.57129649 | 6 | 1.57630126 |
| 2 | 1.57229680 | 7 | 1.57730317 |
| 3 | 1.57329744 | 8 | 1.57830539 |
| 4 | 1.57429840 | 9 | 1.57930793 |
| 5 | 1.57529967 | 10 | 1.58031079 |
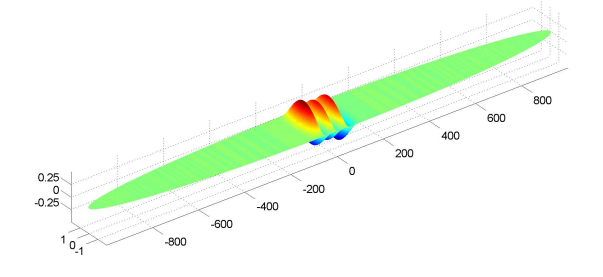
Let us remark that runelip fails to compute the 10 lowest eigenfrequencies. It returns , followed by 4 eigenfrequencies smaller than 1. Such results provide confidence in the validity of our approach.
Example 5
We compare the accuracy of the computed eigenfrequencies if we discretize the Mathieu’s system (1) by the Chebyshev collocation discretization (16) or by the standard finite differences (18). We take , and compute even eigenfrequencies , , and . The errors for the Chebyshev collocation and for the finite differences are collected in Tables 3 and 4, respectively. It is obvious that in spite of better conditioned matrices involved (symmetric, tridiagonal, etc.) finite differences require much larger matrices to obtain accurate results. On the other hand, using the Chebyshev collocation we can compute eigenvalues quite accurately with relatively small matrices.
| error for | error for | error for | |
|---|---|---|---|
| (20,10) | 1.8e-10 | 1.4e-2 | 2.8e-3 |
| (30,15) | 8.1e-14 | 5.9e-6 | 1.4e-4 |
| (40,20) | 9.5e-14 | 3.0e-10 | 8.0e-8 |
| (50,25) | 2.1e-13 | 1.2e-14 | 1.2e-11 |
| error for | error for | error for | |
|---|---|---|---|
| 200 | 5.9e-3 | 5.7e-2 | 3.9e-2 |
| 400 | 3.0e-3 | 2.6e-2 | 1.2e-2 |
| 800 | 1.5e-3 | 1.2e-2 | 4.5e-3 |
| 1600 | 7.4e-4 | 6.0e-3 | 1.8e-3 |
7 Conclusions
The Mathieu’s system as a MEP is accurately solved for domains with geometrical aspect ranging from a circle to very deformed ellipse, i.e. the ratio of the major to minor axes of ellipses equals . This means stability with respect to the geometry of the problem.
Accurate numerical computation of high frequencies is much harder than for low frequencies. We introduced a hierarchy of numerical methods that can deal with the corresponding algebraic eigenvalue problems for increasing , and we are able to compute eigenfrequencies and the corresponding eigenmodes from the first ones to the order of about . However, the accuracy varies from a quasi spectral one for the lowest mode to a moderate one for the highest mode.
With respect to the accuracy as well as to the time required, our algorithm is superior to those reported in literature. It is also stable with respect to the degree of the spectral approximation, i.e. , as is apparent from our reported numerical experiments.
All in all, our novel algorithm can be used to solve the MEP associated to Mathieu’s system corresponding to a large variety of geometrical settings.
References
- [1] F.V. Atkinson, Multiparameter eigenvalue problems, Academic Press, New York, (1972).
- [2] J.P. Boyd, Chebyshev and Fourier Spectral Methods, Springer-Verlag, (1989).
- [3] F.I. Dragomirescu, C.I. Gheorghiu, Analytical and numerical solutions to an electrohydrodynamic stability problem, Appl. Math. Comput., 216, 3718-3727, (2010)
- [4] S.R. Finch. Mathieu eigenvalues. algo.inria.fr/csolve/mthu.pdf, (2008)
- [5] B. Fornberg. A Practical Guide to Pseudospectral Methods, Cambridge University Press, (1998).
- [6] G.H. Golub, C.F. Van Loan. Matrix Computations, 3rd ed., The Johns Hopkins University Press, Baltimore, MD, (1996).
- [7] C.I. Gheorghiu, Spectral Methods for Differential Problems, Casa Cartii de Stiinta, (2007).
- [8] C.I. Gheorghiu, F.I. Dragomirescu. Spectral methods in linear stability. Application to thermal convection with variable gravity field. Appl. Numer. Math. 59, 1290-1302, (2009)
- [9] J. Gutiï¿rrez-Vega, S. Chï¿vez-Cerda, R. Rodriguez-Dagnino. Free oscillations in an elliptic mambrane. Rev. Mex. Fiz., 45,613-622, (1999).
- [10] M.E. Hochstenbach, B. Plestenjak. A Jacobi–Davidson type method for a right definite two-parameter eigenvalue problem. SIAM J. Matrix Anal. Appl., 24, 392–410, (2002).
- [11] M.E. Hochstenbach, B. Plestenjak. Backward error, condition numbers, and pseudospectra for the multiparameter eigenvalue problem. Linear Algebra Appl., 375, 63–81, (2003).
- [12] M.E. Hochstenbach, T. Košir, and B. Plestenjak. A Jacobi–Davidson type method for the nonsingular two-parameter eigenvalue problem, SIAM J. Matrix Anal. Appl., 26, 477–497, (2005).
- [13] M.E. Hochstenbach, B. Plestenjak. Harmonic Rayleigh-Ritz for the multiparameter eigenvalue problem, Electron. Trans. Numer. Anal., 29 81–96, (2008).
- [14] J. Hoepffner. Implementation of boundary conditions. www.fukagata.mech.keio.ac.jp/ jerome/, (2007)
- [15] A. O. Igbokoyi, D. Tiab. New Method of Well Test Analysis in Naturally Fractured Reservoirs Based on Elliptical Flow. JCPT, 49, 1–15,(2010).
- [16] A.G.M. Neves. Eigenmodes and eigenfrequencies of vibrating elliptic membranes: A Klein oscillation theorem and numerical calculations. Commun. Pure Appl. Anal., 9, 611–624, (2004).
- [17] B. Plestenjak. A continuation method for a right definite two-parameter eigenvalue problem, SIAM J. Matrix Anal. Appl., 21, 1163–1184, (2000).
- [18] A. Quarteroni, R. Sacco, F. Saleri. Numerical Mathematics, 2nd ed., Springer Berlin Heidelberg, (2007).
- [19] J. Rommes. Arnoldi and Jacobi-Davidson methods for generalized eigenvalue problems with singular, Math. Comput., 77, 995–1015, (2008).
- [20] L. Ruby, Applications of the Mathieu equation. Am. J. Phys., 64, 39-44, (1996).
- [21] J. Shen, L-L. Wang, On spectral approximation in elliptical geometries using Mathieu functions. Math. Comput., 78, 815-884, (2009).
- [22] B. D. Sleeman, Multiparameter spectral theory and separation of variables. J. Phys. A: Math. Theor. 41, (2008)015209
- [23] L.N. Trefethen, Spectral Methods in MATLAB, SIAM, (2000).
- [24] B. A. Troesch, H. R. Troesch, Eigenfrequencies of an Elliptic Membrane, Math. Comput., 27, 755-765, (1973)
- [25] H. Volkmer, Multiparameter Problems and Expansion Theorems, Lecture Notes in Math. 1356, Springer-Verlag, New-York, (1988)
- [26] J.A.C. Weideman, S.C. Reddy. A MATLAB differentiation matrix suite. ACM Trans. Math. Softw., 26, 465–519, (2000)
- [27] H. B. Wilson. Vibration modes of an elliptic membrane. Available from http://www.mathworks.com/matlabcentral/fileexchange. MATLAB File Exchange, The MathWorks, Natick, (2004).
- [28] H. B. Wilson, R. W. Scharstein, Computing elliptic membrane high frequencies by Mathieu and Galerkin methods, J. Eng. Math, 57, 41-55, (2007)
- [29] H. B. Wilson, L. S. Turcotte, D. Halpern. Advanced Mathematics and Mechanics Applications Using MATLAB, 3rd ed., Boca Raton: Chapman and Hall/CRC, (2003).
[1] H. Volkmer, Multiparameter Problems and Expansion Theorems, Lecture Notes in Math. 1356, Springer-Verlag, New York, 1988.
[2] J. Meixner, F. W. Schafke, Mathieusche Funktionen und Spharoidfunktionen, Springer-Verlag, 1954.
[3] L. Ruby, Applications of the Mathieu equation, Am. J. Phys. 64 (1996) 39–44.
[4] A. O. Igbokoyi, D. Tiab, New method of well test analysis in naturally fractured reservoirs based on elliptical flow, J. Can. Pet. Technol. 49 (2010) 1–15.
[5] A. G. M. Neves, Eigenmodes and eigenfrequencies of vibrating elliptic membranes: A Klein oscillation theorem and numerical calculations, Commun. Pure Appl. Anal. 9 (2004) 611–624.
[6] B. A. Troesch, H. R. Troesch, Eigenfrequencies of an elliptic membrane, Math. Comput. 27 (1973) 755–765.
[7] J. Gutierrez-Vega, S. Chavez-Cerda, R. Rodrıguez-Dagnino, Free oscillations in an elliptic mambrane, Rev. Mex. Fiz. 45 (1999) 613–622.
[8] H. B. Wilson, R. W. Scharstein, Computing elliptic membrane high frequencies by Mathieu and Galerkin methods, J. Eng. Math. 57 (2007) 41– 55.
[9] L. N. Trefethen, Spectral Methods in MATLAB, SIAM, Philadelphia, 2000.
[10] J. A. C. Weideman, S. C. Reddy, A MATLAB differentiation matrix suite, ACM Trans. Math. Softw. 26 (2000) 465–519.
[11] J. P. Boyd, Chebyshev and Fourier Spectral Methods, Lecture Notes in Engineering 49, Springer-Verlag, Berlin, 1989.
[12] J. Shen, L-L. Wang, On spectral approximation in elliptical geometries using Mathieu functions, Math. Comput. 78 (2009) 815–884.
[13] S. R. Finch, Mathieu eigenvalues, algo.inria.fr/csolve/mthu.pdf (2008).
[14] B. D. Sleeman, Multiparameter spectral theory and separation of variables, J. Phys. A: Math. Theor. 41 (2008) 1–20.
[15] F. V. Atkinson, Multiparameter Eigenvalue Problems, Academic Press, New York, 1972.
[16] M. E. Hochstenbach, T. Kosir, B. Plestenjak, A Jacobi–Davidson type method for the nonsingular two-parameter eigenvalue problem, SIAM J. Matrix Anal. Appl. 26 (2005) 477–497.
[17] B. Plestenjak, A continuation method for a right definite two-parameter eigenvalue problem, SIAM J. Matrix Anal. Appl. 21 (2000) 1163–1184.
[18] G. H. Golub, C. F. Van Loan, Matrix Computations, third ed., The Johns Hopkins University Press, Baltimore, 1996.
[19] M. E. Hochstenbach, B. Plestenjak, Harmonic Rayleigh-Ritz for the multiparameter eigenvalue problem, Electron. Trans. Numer. Anal. 29 (2008) 81–96.
[20] J. Rommes, Arnoldi and Jacobi-Davidson methods for generalized eigenvalue problems Ax = λBx with B singular, Math. Comput. 77 (2008) 995–1015.
[21] F. I. Dragomirescu, C. I. Gheorghiu, Analytical and numerical solutions to an electrohydrodynamic stability problem, Appl. Math. Comput. 216 (2010) 3718–3727.
[22] C. I. Gheorghiu, Spectral Methods for Differential Problems, Casa Cartii de Stiinta, Cluj-Napoca, 2007.
[23] C. I. Gheorghiu, F. I. Dragomirescu, Spectral methods in linear stability. Application to thermal convection with variable gravity field, Appl. Numer. Math. 59 (2009) 1290–1302.
[24] B. Fornberg, A Practical Guide to Pseudospectral Methods, Cambridge University Press, Cambridge, 1998.
[25] J. Hoepffner, Implementation of boundary conditions, www.fukagata. mech.keio.ac.jp/~jerome/ (2007).
[26] M. E. Hochstenbach, B. Plestenjak, Backward error, condition numbers, and pseudospectra for the multiparameter eigenvalue problem, Lin. Alg. Appl. 375 (2003) 63–81.
[27] A. Quarteroni, R. Sacco, F. Saleri, Numerical Mathematics, second ed., Texts in Applied Mathematics 47, Springer, Berlin Heidelberg, 2007.
[28] H. B. Wilson, L. S. Turcotte, D. Halpern, Advanced Mathematics and Mechanics Applications Using MATLAB, third ed., Chapman and Hall/CRC, Boca Raton, 2003.
[29] H. B. Wilson, Vibration modes of an elliptic membrane. Available from http://www.mathworks.com/matlabcentral/fileexchange. MATLAB File Exchange, The MathWorks, Natick, 2004.
