Abstract
We obtain new univariate Shepard operators using polynomials that are constructed such that they fit the interpolation data in a weighted least squares approximation way. We study the degree of exactness, the linearity and the remainder for the corresponding interpolation formula.
Authors
Andra Malina
Faculty of Mathematics and Computer Science, Babeş-Bolyai University, Cluj-Napoca, Romania
Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy, Cluj-Napoca, Romania
Keywords
Univariate Shepard operator; Weighted least squares approximation; Interpolation formula; Degree of exactness; Remainder term
Paper coordinates
A. Malina, Univariate Shepard operators combined with least squares fitting polynomials, Filomat, 38 (2024) no. 15, pp. 5507-5516. https://doi.org/10.2298/FIL2415507M
About this paper
Journal
Filomat
Publisher Name
Faculty of Sciences and Mathematics, University of Nis, Serbia
Print ISSN
0354-5180
Online ISSN
2406-0933
google scholar link
Paper (preprint) in HTML form
Univariate Shepard operators combined with least squares fitting polynomials
Abstract
We obtain new univariate Shepard operators using polynomials that are constructed such that they fit the interpolation data in a weighted least squares approximation way. We study the degree of exactness, the linearity and the remainder for the corresponding interpolation formula.
1 Introduction
D. Shepard introduced in 1968 in [13] a very powerful method for approximating a given function on a set of scattered data, method that nowadays is named after him. The procedure has an easy implementation and it is expressed as a combination between some basis functions and the values of the function on a given set of interpolation nodes. However, two of its major drawbacks are the high computational cost and the low degree of exactness. Several authors have studied them and proposed different solutions to overcome them, such as modifying the basis functions or combining the Shepard operator with other interpolation operators for an increased degree of exactness (see, e.g., [1]; [2]; [3]; [4]; [5]; [6]; [7]; [8]; [9]; [10]).
In the univariate case, when is a real-valued function defined on a subset of , for a given set of interpolation nodes, , the Shepard operator is defined as
| (1) |
with the basis functions given by
| (2) |
and an arbitrary parameter.
This paper focuses on introducing a new univariate Shepard operator, combined with polynomials constructed based on the least squares approach. In Section 2, after we construct these polynomials, we study several properties of them and of the combined Shepard operators (interpolation property, degree of exactness, linearity). Finally, we study the errors, based on Peano’s Theorem. Section 3 is dedicated to numerical examples that show the benefits of these Shepard operators.
2 Shepard operators combined with polynomials constructed by the least squares method
R. J. Renka introduced in 1988 in [11] an algorithm for improving the bivariate Shepard operator, considering a quadratic polynomial that interpolates the function on a set of given nodes and also approximates the data in a weighted least squares way. Later on, in 1999 in [12] he improved this method by replacing the quadratic polynomial with a cubic one. In 2010 in [14], W. I. Thacker et al. emphasized the main disadvantages of these two methods and suggested the combination of the Shepard operator with a linear polynomial that still fits the data in a weighted least squares sense.
Using some ideas for the bivariate case presented in the above mentioned papers, we are going to consider an improvement for the classical Shepard operator in the univariate case, by combining it with polynomials of degree , constructed following the weighted least squares approximation technique.
Consider , and given real nodes, denoted by , . The values of the function on the given nodes are known and denoted by .
Under these assumptions, for a point , let us define the th degree polynomial function , , , as
| (3) |
where the coefficients are found such that they minimize the sum of the weighted squared residuals
| (4) |
where
| (5) |
for and .
In order to find the coefficients (i.e, obtain the minimum of expression (4)), we follow the weighted least squares reasoning, take the partial derivatives of with respect to each unknown, set them to zero and solve the resulting system:
Further, for every one obtains
Let us make the notation
Then, the system of normal equations that has to be solved in order to find the coefficients has the form
| (6) |
for each .
For every we can write the normal equations that appear above in a matricial form as
| (7) |
where is a matrix having on the entry the element , is a vector of elements with on the th entry and is the vector of unknowns.
Theorem 2.1
The operator defined in (3) satisfies the following interpolation property
Proof 2.2.
For any , one has
Theorem 2.3.
The operator , has the degree of exactness n, i.e.,
where ”” denotes the degree of exactness.
Proof 2.4.
For we have the following cases for :
-
Case 1.
. We get , and obviously
-
Case 2.
. We obtain the following solution for the coefficients :
(8) and
-
Case 3.
. In this situation we have
and
-
Case 4.
. It is obvious that since
and no term appears.
In conclusion, .
Theorem 2.5.
The operator is linear.
Proof 2.6.
Definition 2.7.
Theorem 2.8.
The following interpolation property holds
Theorem 2.10.
The operator is linear.
Proof 2.11.
For arbitrarily chosen and , using the linearity of showed in Theorem 2.5, one has
the linearity of being proved.
Theorem 2.12.
The Shepard operator has degree of exactness n.
Proof 2.13.
We know that for some arbitrary operators , with we have , where
Taking into account this property and the fact that , we obtain the desired conclusion.
We now introduce the interpolation formula for the univariate Shepard combined with a polynomial, that is given by
with denoting the remainder.
Considering the space , of functions (continuously differentiable up to order , inclusively) with absolutely continuous on , we obtain the following result for the remainder of the formula:
Theorem 2.14.
Proof 2.15.
The degree of exactness for the Shepard operator is n. Using now the Peano’s theorem, one gets
with
Finally, for all , we obtain
where are solutions of , for each , for
concluding in this way the proof.
3 Test results
For the numerical experiments we consider four well-known real-valued test functions (see, e.g., [9]):
| (13) |
For each function , we compare the test results obtained by considering the linear, quadratic and cubic interpolants with the ones obtained for some other combined Shepard operators, well-known in the literature. We study the maximum approximation errors for the Shepard operators of Lagrange, Taylor and Bernoulli type, for all of them considering the first, second and third order. They are denoted by and , , respectively. We recall their definitions in the sequel.
3.1 Univariate Shepard-Lagrange operator (see, e.g., [5])
For distinct points that belong to and the real-valued function defined on such that the data are known, the univariate Shepard-Lagrange operator is defined as
| (14) |
with
| (15) |
and defined in (2), .
3.2 Univariate Shepard-Taylor operator (see, e.g., [5])
For and distinct interpolation nodes , consider the sets
and
such that is a subset of associated to , having , for all .
3.3 Univariate Shepard-Bernoulli operator (see, e.g., [6])
Suppose there are given points in and . Then, we can define the univariate Shepard-Bernoulli operator as follows
| (18) |
with defined in (2) and the Bernoulli operators given by
for , .
are the Bernoulli numbers, i.e. the values of the Bernoulli polynomials at . The Bernoulli polynomials are defined recursively as
We consider a set of equally spaced interpolation nodes from the interval and set the parameter’s value to . Table 1 presents the maximum interpolation errors for the classical Shepard operator introduced in (1) and the linear , quadratic and cubic Shepard operators, introduced in (10) for , respectively. In addition, we present the maximum approximation errors for the Shepard operators of Lagrange, Taylor and Bernoulli type, of order 1, 2 and 3, respectively. We can observe that the three new operators produce better approximation results than the classical Shepard operator. Moreover, as it was expected, higher degrees polynomials produce smaller approximation errors. We can observe that in the linear and quadratic cases, the approximation results for the Shepard operators combined with least squares fitting polynomials are close to the best approximation results for most of the functions. In the cubic cases the new Shepard operators obtained produce the smallest interpolation errors.
| 0.0247 | 0.0043 | 0.0024 | 0.0084 | |
| 0.0157 | 0.0025 | 0.0024 | 0.0041 | |
| 0.0081 | 0.0020 | 0.0013 | 0.0030 | |
| 0.0067 | 0.0020 | 0.0012 | 0.0027 | |
| 0.0081 | 0.0020 | 0.0013 | 0.0030 | |
| 0.0066 | 0.0012 | 8.7983e-04 | 0.0041 | |
| 0.0048 | 9.4582e-04 | 0.0014 | 0.0027 | |
| 0.0050 | 0.0010 | 7.7720e-04 | 0.0026 | |
| 0.0048 | 0.0010 | 7.7771e-04 | 0.0027 | |
| 0.0053 | 5.4032e-04 | 6.7304e-04 | 0.0023 | |
| 0.0671 | 0.0050 | 0.0049 | 0.0024 | |
| 0.0094 | 8.7148e-04 | 8.7393e-04 | 0.0024 | |
| 0.0104 | 8.8533e-04 | 8.7689e-04 | 0.0024 |
We also test these operators on a second set of Chebyshev nodes, defined as
We present the maximum approximation errors in Table 2. In this case we can see that the new operators produce the best results in the quadratic case for all the functions, except for . In the cubic case they produce the smallest interpolation errors for all test functions. Very good results are obtained in the linear case as well.
| 0.0246 | 0.0064 | 0.0046 | 0.0160 | |
| 0.0119 | 0.0018 | 0.0019 | 0.0066 | |
| 0.0078 | 0.0034 | 0.0016 | 0.0031 | |
| 0.0094 | 0.0035 | 0.0017 | 0.0021 | |
| 0.0083 | 0.0035 | 0.0016 | 0.0031 | |
| 0.0054 | 9.3156e-04 | 0.0011 | 0.0065 | |
| 0.0119 | 0.0027 | 0.0013 | 0.0040 | |
| 0.0139 | 0.0029 | 0.0015 | 0.0037 | |
| 0.0133 | 0.0029 | 0.0015 | 0.0038 | |
| 0.0046 | 2.6850e-04 | 7.0098e-04 | 0.0027 | |
| 0.0070 | 7.3503e-04 | 7.9055e-04 | 0.0051 | |
| 0.0089 | 9.3807e-04 | 9.8040e-04 | 0.0054 | |
| 0.0082 | 9.3521e-04 | 9.8137e-04 | 0.0054 |
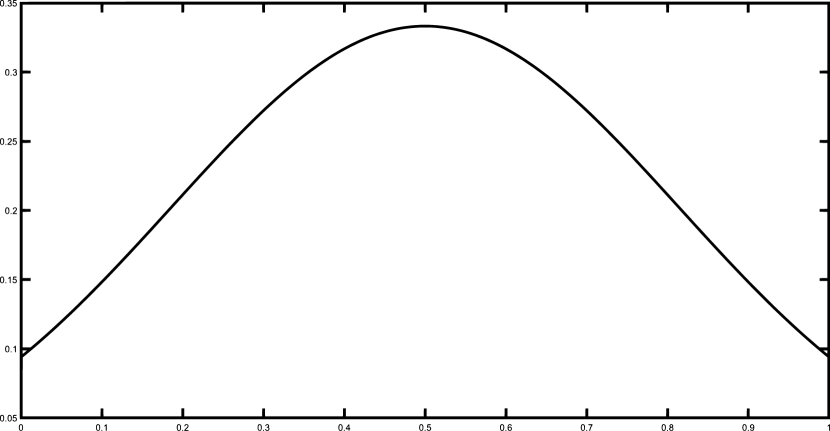
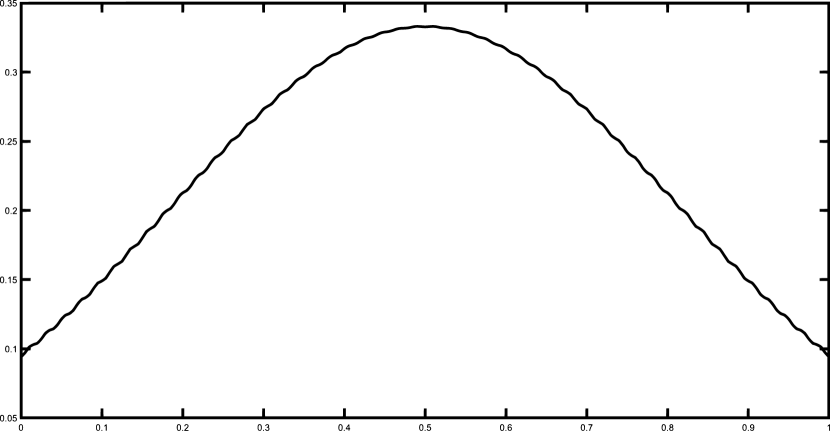
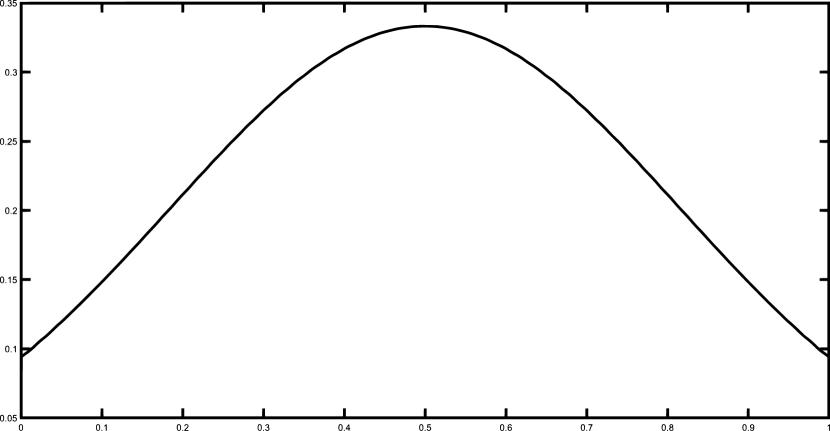
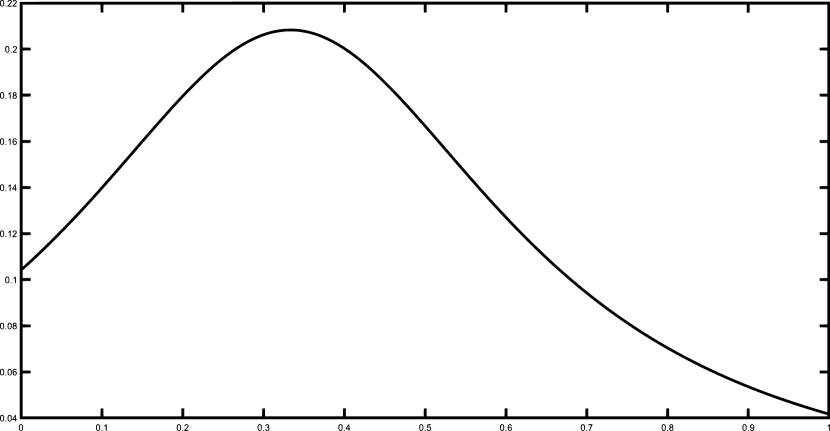
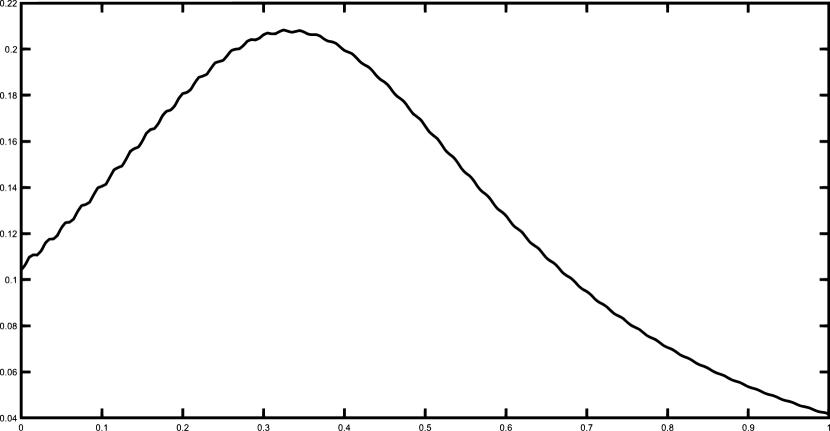
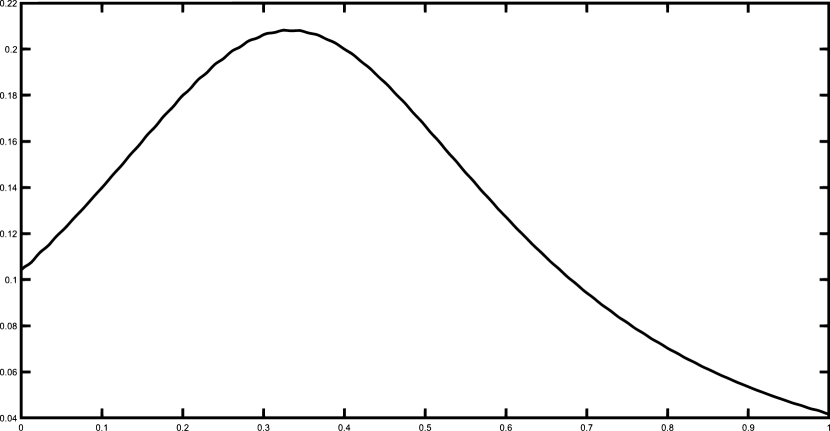
Finally, we present the graphical results for the Gentle and the Saddle functions using the set of 50 equally spaced nodes. Figures 1–2 illustrates the functions and and their corresponding polynomial Shepard interpolants and .


References
- (1) R. Caira, F. Dell’Accio, Shepard-Bernoulli operators, Math. Comp. 76 (2007), 299–321.
- (2) T. Cătinaş, The combined Shepard-Abel-Goncharov univariate operator, J. Numer. Anal. Approx. Theory 32 (2003), 11–20.
- (3) Gh. Coman, Combined Shepard univariate operators, East J. Approx. 7 (2001), 471–483.
- (4) Gh. Coman, R. Trîmbiţaş, Univariate Shepard-Birkhoff interpolation, J. Numer. Anal. Approx. Theory 30 (2001), 15–24.
- (5) Gh. Coman, R. Trîmbiţaş, Combined Shepard univariate operators, East J. Approx. 7 (2001), 471–483.
- (6) F. Dell’Accio, F. Di Tommaso, Scattered data interpolation by Shepard’s like methods: classical results and recent advances, Dolomites Res. Notes Approx. 9 (2016), 32–44.
- (7) R. Franke, Scattered data interpolation: tests of some methods, Math. Comp. 38 (1982), 181–200.
- (8) R. Franke, G. Nielson, Smooth interpolation of large sets of scattered data, Internat. J. Numer. Methods Engrg. 15 (1980), 1691–1704.
- (9) R.J. Renka, A.K. Cline, A triangle-based interpolation method, Rocky Mountain J. Math. 14 (1984), 223–237.
- (10) R.J. Renka, Multivariate interpolation of large sets of scattered data, ACM Trans. Math. Software 14 (1988), 139–148.
- (11) R.J. Renka, Algorithm 660: QSHEP2D: Quadratic method for bivariate interpolation of scattered data, ACM Trans. Math. Software 14 (1988), 149–150.
- (12) R.J. Renka, Algorithm 790: CSHEP2D: Cubic method for bivariate interpolation of scattered data, ACM Trans. Math. Software 25 (1999), 70–73.
- (13) D. Shepard, A two dimensional interpolation function for irregularly spaced data, In: Proceedings of 23rd National Conference ACM (1968), 517–523.
- (14) W. Thacker, J. Zhang, L. Watson, J. Birch, M. Iyer, M. Berry, Algorithm 905: SHEPPACK: Modified Shepard algorithm for interpolation of scattered multivariate data, ACM Trans. Math. Software 37 (2010), 1–20.
[1] R. Caira, F. Dell’Accio, Shepard-Bernoulli operators, Math. Comp. 76 (2007), 299–321.
[2] T. Cătinaș, The combined Shepard-Abel-Goncharov univariate operator, J. Numer. Anal. Approx. Theory 32 (2003), 11–20.
[3] Gh. Coman, Combined Shepard univariate operators, East J. Approx. 7 (2001), 471–483.
[4] Gh. Coman, R. Trîmbițaș, Univariate Shepard-Birkhoff interpolation, J. Numer. Anal. Approx. Theory 30 (2001), 15–24.
[5] Gh. Coman, R. Trîmbițaș, Combined Shepard univariate operators, East J. Approx. 7 (2001), 471–483.
[6] F. Dell’Accio, F. Di Tommaso, Scattered data interpolation by Shepard’s like methods: classical results and recent advances, Dolomites Res. Notes Approx. 9 (2016), 32–44.
[7] R. Franke, Scattered data interpolation: tests of some methods, Math. Comp. 38 (1982), 181–200.
[8] R. Franke, G. Nielson, Smooth interpolation of large sets of scattered data, Internat. J. Numer. Methods Engrg. 15 (1980), 1691–1704.
[9] R.J. Renka, A.K. Cline, A triangle-based C1 interpolation method, Rocky Mountain J. Math. 14 (1984), 223–237.
[10] R.J. Renka, Multivariate interpolation of large sets of scattered data, ACM Trans. Math. Software 14 (1988), 139–148.
[11] R.J. Renka, Algorithm 660: QSHEP2D: Quadratic method for bivariate interpolation of scattered data, ACM Trans. Math. Software 14 (1988), 149–150.
[12] R.J. Renka, Algorithm 790: CSHEP2D: Cubic method for bivariate interpolation of scattered data, ACM Trans. Math. Software 25 (1999), 70–73.
[13] D. Shepard, A two dimensional interpolation function for irregularly spaced data, In: Proceedings of 23rd National Conference ACM (1968), 517–523.
[14] W. Thacker, J. Zhang, L. Watson, J. Birch, M. Iyer, M. Berry, Algorithm 905: SHEPPACK: Modified Shepard algorithm for interpolation of scattered multivariate data, ACM Trans. Math. Software 37 (2010), 1–20.
