[1] Massabó et al. [2008] derived useful first-order estimations of ergodic dispersivities for transport of kinetically sorbing solutes in heterogeneous porous media with bimodal hydraulic conductivity distributions. Such dispersivity estimates can serve as comparison terms and, in case of infinite domains, they also can be used as input parameters of transport operator for multicomponent transport-reaction problems in heterogeneous porous media [Kräutle and Knabner, 2005, 2007]. In this commentary we try to establish conditions for the applicability of the ergodic parameters obtained by Massabó et al. [2008] to real cases corresponding to single-realizations of the stochastic models.
[2] Massabó et al. [2008, paragraph 20] claim that "a well established result of stochastic theories is that for plumes with transverse dimension much larger than the corresponding integral scale, transport develops under ergodic conditions" and the single realization dispersion $s_{lm}$$s_{lm}$s_(lm)s_{l m}$s_{lm}$ can be approximated by the sum between the second moment of the initial plume $S_{lm}(0)$$S_{lm}(0)$S_(lm)(0)S_{l m}(0)$S_{lm}(0)$ and the one-particle dispersion $X_{lm}$$X_{lm}$X_(lm)X_{l m}$X_{lm}$, where $l$$l$ll$l$ and $m$$m$mm$m$ range between 1 and the dimensionality of the problem:

In our recent paper [Suciu et al., 2008], however, it is shown that the above statement is not entirely true. At finite times, ergodicity can be obtained under suitable initial conditions for either longitudinal or transverse dispersion but not for both of them. If a local dispersion process is considered, then ergodicity holds asymptotically for both longitudinal and transverse dispersion and for the cross-section average concentration [Suciu et al., 2006a].
[3] For plumes with initial dimensions larger than the heterogeneity scale, the variance of the plume center of mass can be neglected [Suciu et al., 2008, Figure 1] and relation (1) holds for the ensemble average of $S_{lm}=⟨s_{lm}⟩$$S_{lm}=⟨s_{lm}⟩$S_(lm)=(:s_(lm):)S_{l m}=\left\langle s_{l m}\right\rangle$S_{lm}=⟨s_{lm}⟩$ of the single realization dispersion. To show that (1) is not a valid approximation for single realizations we consider advection-dispersion processes $\mathbf{X}(t,{\mathbf{X}}_0)$$\mathbf{X}\left(t,{\mathbf{X}}_0\right)$X(t,X_(0))\mathbf{X}\left(t, \mathbf{X}_{0}\right)$\mathbf{X}(t,{\mathbf{X}}_0)$ starting at $t=0$$t=0$t=0t=0$t=0$

from different initial positions ${\mathbf{X}}_0$${\mathbf{X}}_0$X_(0)\mathbf{X}_{0}${\mathbf{X}}_0$ and the diagonal components $ll$$ll$lll l$ll$ of the dispersion. For a fixed realization of the velocity, the dispersion of the molecules at a given time $s_{ll}={⟨{[X_l-{⟨X_l⟩}_{D{X}_0}]}^2⟩}_{D{X}_0}$$s_{ll}={⟨{\left[X_l-{⟨X_l⟩}_{D{X}_0}\right]}^2⟩}_{D{X}_0}$s_(ll)=(:[X_(l)-(:X_(l):)_(DX_(0))]^(2):)_(DX_(0))s_{l l}= \left\langle\left[X_{l}-\left\langle X_{l}\right\rangle_{D X_{0}}\right]^{2}\right\rangle_{D X_{0}}$s_{ll}={⟨{[X_l-{⟨X_l⟩}_{D{X}_0}]}^2⟩}_{D{X}_0}$ can be expressed as
$$\begin{array}{rl}{s}_{ll}=& S_{ll}(0)+{⟨{[{\tilde{X}}_l-{⟨{\tilde{X}}_l⟩}_{D{X}_0}]}^2⟩}_{D{X}_0}\\ \text{(2)}& & +2{⟨[X_{0l}-{⟨X_{0l}⟩}_{X_0}]{⟨{\tilde{X}}_l⟩}_D⟩}_{X_0},\end{array}$$$$\begin{array}{r}{s}_{ll}=S_{ll}(0)+{⟨{\left[{\tilde{X}}_l-{⟨{\tilde{X}}_l⟩}_{D{X}_0}\right]}^2⟩}_{D{X}_0}\\ \text{(2)}& & +2{⟨\left[X_{0l}-{⟨X_{0l}⟩}_{X_0}\right]{⟨{\tilde{X}}_l⟩}_D⟩}_{X_0},\end{array}$${:[s_(ll)=S_(ll)(0)+(:[ widetilde(X)_(l)-(: widetilde(X)_(l):)_(DX_(0))]^(2):)_(DX_(0))],[(2)+2(:[X_(0l)-(:X_(0l):)_(X_(0))](: widetilde(X)_(l):)_(D):)_(X_(0))","]:}\begin{align*} s_{l l}= & S_{l l}(0)+\left\langle\left[\widetilde{X}_{l}-\left\langle\widetilde{X}_{l}\right\rangle_{D X_{0}}\right]^{2}\right\rangle_{D X_{0}} \\ & +2\left\langle\left[X_{0 l}-\left\langle X_{0 l}\right\rangle_{X_{0}}\right]\left\langle\widetilde{X}_{l}\right\rangle_{D}\right\rangle_{X_{0}}, \tag{2} \end{align*}$$\begin{array}{rl}{s}_{ll}=& S_{ll}(0)+{⟨{[{\tilde{X}}_l-{⟨{\tilde{X}}_l⟩}_{D{X}_0}]}^2⟩}_{D{X}_0}\\ \text{(2)}& & +2{⟨[X_{0l}-{⟨X_{0l}⟩}_{X_0}]{⟨{\tilde{X}}_l⟩}_D⟩}_{X_0},\end{array}$$
where the subscripts $D$$D$DD$D$ and $X_0$$X_0$X_(0)X_{0}$X_0$ in (2) denote respectively the average over the realizations of the local dispersion and the space average with respect to the initial distribution of molecules and $X_l=X_l-X_{0l}$$X_l=X_l-X_{0l}$X_(l)=X_(l)-X_(0l)X_{l}=X_{l}-X_{0 l}$X_l=X_l-X_{0l}$ [Suciu et al., 2008]. The last term in (2) is a memory term $m_{ll}$$m_{ll}$m_(ll)m_{l l}$m_{ll}$ describing spatial correlations between relative displacements on trajectories and initial positions. The case of vanishing local dispersion, described by the relation (2) without subscript $D$$D$DD$D$, was investigated by Sposito and Dagan [1994]. Implications of memory terms for transport in inhomogeneous velocity fields were briefly discussed by Suciu and Vamoş [2007].
[4] Arguments based on the ergodicity of the random velocity field suggest that space averages over the initial positions can be replaced by ensemble averages. Then, the second term of (2) is an ergodic estimation of the oneparticle dispersion $X_{ll}$$X_{ll}$X_(ll)X_{l l}$X_{ll}$ and the actual dispersion (2) becomes
$$\begin{array}{}\text{(3)}& s_{ll}\approx S_{ll}(0)+X_{ll}+m_{ll}\end{array}$$$$\begin{array}{}\text{(3)}& s_{ll}\approx S_{ll}(0)+X_{ll}+m_{ll}\end{array}$${:(3)s_(ll)~~S_(ll)(0)+X_(ll)+m_(ll):}\begin{equation*} s_{l l} \approx S_{l l}(0)+X_{l l}+m_{l l} \tag{3} \end{equation*}$$\begin{array}{}\text{(3)}& s_{ll}\approx S_{ll}(0)+X_{ll}+m_{ll}\end{array}$$
[5] The relevance of the stochastic description for the dispersion observable in a real case is an ergodic property in a broader sense that cannot be reduced to that of the random space function describing the velocity field [Suciu et al., 2006a; Suciu and Vamoş, 2007]. This property can be quantified by an "ergodicity range" defined as root mean square deviation of observable quantities from stochastic model predictions [Suciu et al., 2006a]. For large initial plumes the ergodicity range of $s_{ll}-S_{ll}(0)$$s_{ll}-S_{ll}(0)$s_(ll)-S_(ll)(0)s_{l l}-S_{l l}(0)$s_{ll}-S_{ll}(0)$ with respect to $X_{ll}$$X_{ll}$X_(ll)X_{l l}$X_{ll}$ can be estimated, according to (3), by standard deviations of memory terms $m_{ll}$$m_{ll}$m_(ll)m_{l l}$m_{ll}$. This statement is supported by the numerical experiment on the basis of the "global random walk" algorithm [Vamoş et al., 2003], presented by Suciu et al. [2006a, 2008].
[6] The numerical experiment was carried out under conditions that are usually assumed in first-order approximation approaches: an isotropic two-dimensional aquifer system with statistically homogeneous log-hydraulic con-

ductivity of small variance equal to 0.1 and exponentially decaying correlation with correlation length $\lambda =1\mathrm{m}$$\lambda =1\mathrm{m}$lambda=1m\lambda=1 \mathrm{~m}$\lambda =1\mathrm{m}$, firstorder approximations of Darcy flow with mean flow velocity $U=1\mathrm{m}/\mathrm{d}$$U=1\mathrm{m}/\mathrm{d}$U=1m//dU=1 \mathrm{~m} / \mathrm{d}$U=1\mathrm{m}/\mathrm{d}$, and isotropic local dispersion with constant coefficient $D=0.01{\mathrm{m}}^2/\mathrm{d}$$D=0.01{\mathrm{m}}^2/\mathrm{d}$D=0.01m^(2)//dD=0.01 \mathrm{~m}^{2} / \mathrm{d}$D=0.01{\mathrm{m}}^2/\mathrm{d}$. The accuracy was ensured by using 6400 periodic modes in the Kraichnan procedure to generate the velocity fields, by tracking in every velocity realization ${10}^{10}$${10}^{10}$10^(10)10^{10}${10}^{10}$ particles with the global random walk algorithm, and by averaging over 1024 realizations of the velocity field.
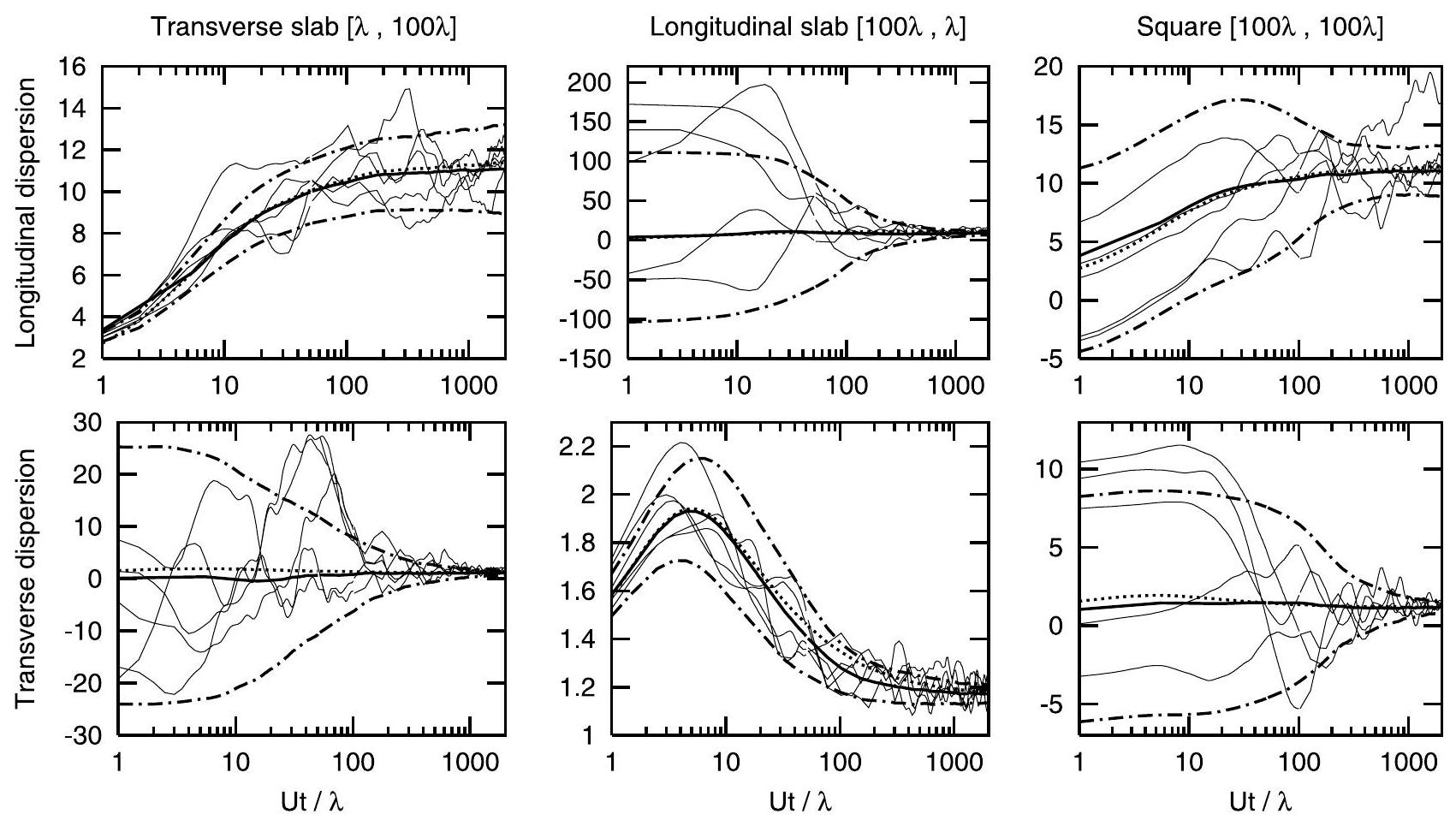
[7] Since in a consistent first-order approximation with leading term given by the ensemble mean displacement the advective and dispersive displacements decouple [Suciu et al [2006b, equation (7)], the results of Massabó et al. [2008] can be extended to the dispersive case by simply adding the local dispersion coefficients in their equation (19). Hence, the numerical experiment can be compared with the unimodal case considered by Massabó et al. [2008]. The differences between the cases of unimodal and bimodal hydraulic conductivity distributions [Massabó et al., 2008, Figures 1 and 6] are small as compared with the ergodicity ranges we present in the following. Therefore, we consider that the numerical results are relevant for the bimodal case as well. The two processes considered by the authors (the Markov chain describing the time spent by particles in the mobile phase and the space random hydraulic conductivity) are independent. Therefore, the ergodicity ranges of the reactive problem should be at least as large as those of the nonreactive case considered in the numerical experiment.
[8] Figure 1 summarizes results on ergodicity of the longitudinal and transverse dispersion for large sources consisting of transverse and longitudinal slabs and a square, with dimensions of 100 correlation scales $\lambda$$\lambda$lambda\lambda$\lambda$ of the log-
hydraulic conductivity. Since the deviation of the ensemble average dispersion $[S_{ll}-S_{ll}(0)]$$\left[S_{ll}-S_{ll}(0)\right]$[S_(ll)-S_(ll)(0)]\left[S_{l l}-S_{l l}(0)\right]$[S_{ll}-S_{ll}(0)]$ from the one-particle dispersion $X_{ll}$$X_{ll}$X_(ll)X_{l l}$X_{ll}$ is very small, the ergodicity range practically coincides with the standard deviation $SD\left(s_{ll}\right)\approx SD\left(m_{ll}\right)$$SD\left(s_{ll}\right)\approx SD\left(m_{ll}\right)$SD(s_(ll))~~SD(m_(ll))S D\left(s_{l l}\right) \approx S D\left(m_{l l}\right)$SD\left(s_{ll}\right)\approx SD\left(m_{ll}\right)$, in agreement with the heuristic relation (3). Acceptable small ergodicity ranges of both longitudinal and transverse dispersion are expected only after hundreds of dimensionless times $Ut/\lambda$$Ut/\lambda$Ut//lambdaU t / \lambda$Ut/\lambda$. At early times smaller than $100Ut/\lambda$$100Ut/\lambda$100 Ut//lambda100 U t / \lambda$100Ut/\lambda$, ergodic longitudinal dispersion can be obtained for large transverse slab sources and ergodic transverse dispersion for large longitudinal slabs. It is also obvious from the comparison of the six cases presented in Figure 1 that ergodicity of both longitudinal and transverse dispersion cannot be reached at early times for the same initial conditions.
[9] Concluding, we suggest that dispersivities derived from first-order approximations of the one-particle dispersion by Massabó et al. [2008, equation (19)] can be used for modeling the transport at large travel distances, when accompanied by uncertainty estimates given by the corresponding ergodicity ranges (see Figure 1). We also suggest that it is possible to use the longitudinal ergodic dispersivity, for large transverse slab sources, in problems for crosssection space average concentration [see, e.g., Suciu et al., 2006a].
[10] Acknowledgments. This work was supported by Deutsche Forschungsgemeinschaft grant SU 415/1-2.

Kräutle, S., and P. Knabner (2005), A new numerical reduction scheme for fully coupled multicomponent transport-reaction problems in porous media, Water Resour. Res., 41, W09414, doi:10.1029/2004WR003624.
Kräutle, S., and P. Knabner (2007), A reduction scheme for coupled multicomponent transport-reaction problems in porous media: Generalization
to problems with heterogeneous equilibrium reactions, Water Resour. Res., 43, W03429, doi:10.1029/2005WR004465.
Massabó, M., A. Bellin, and A. J. Valocchi (2008), Spatial moments analysis of kinetically sorbing solutes in aquifer with bimodal permeability distribution, Water Resour. Res., 44, W09424, doi:10.1029/ 2007WR006539.
Sposito, G., and G. Dagan (1994), Predicting solute plume evolution in heterogeneous porous formations, Water Resour. Res., 30(2), 585-589.
Suciu, N., and C. Vamoş (2007), Comment on "Nonstationary flow and nonergodic transport in random porous media" by G. Darvini and P. Salandin, Water Resour. Res., 43, W12601, doi:10.1029/2007WR005946.
Suciu, N., C. Vamoș, J. Vanderborght, H. Hardelauf, and H. Vereecken (2006a), Numerical investigations on ergodicity of solute transport in heterogeneous aquifers, Water Resour. Res., 42, W04409, doi:10.1029/ 2005WR004546.

Suciu, N., C. Vamoş, and J. Eberhard (2006b), Evaluation of the first-order approximations for transport in heterogeneous media, Water Resour. Res., 42, W11504, doi:10.1029/2005WR004714.
Suciu, N., C. Vamoş, H. Vereecken, K. Sabelfeld, and P. Knabner (2008), Memory effects induced by dependence on initial conditions and ergodicity of transport in heterogeneous media, Water Resour. Res., 44, W08501, doi:10.1029/2007WR006740.
Vamoş, C., N. Suciu, and H. Vereecken (2003), Generalized random walk algorithm for the numerical modeling of complex diffusion processes, J. Comput. Phys., 186(2), 527-544, doi:10.1016/S0021-9991(03)00073-1.