Iterative Shepard operator of least squares thin-plate spline type

Malina Andra Babeş-Bolyai University, Faculty of Mathematics and Computer Science & Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy, Cluj-Napoca, Romania

Abstract

We propose a modified bivariate Shepard operator of least squares thin-plate spline type based on an iterative method, introduced by A.V. Masjukov and V.V. Masjukov. This iterative method does not require an artificial setup of the parameters and it is based on successive scaling. For the numerical examples, using an idea of J. R. McMahon, we construct some representative sets of knot points for the initial sets of the interpolation nodes.

^†^†volume: 7

Keywords: Shepard operator, least squares approximation, thin-plate spline, knot points, iterative multiscale method.

2010 Mathematics Subject Classification: 41A05, 41A25.

1 Preliminaries

The Shepard method, introduced by D. Shepard in [16], is one of the best suited methods for interpolating scattered data. It has many computational advantages and many of its drawbacks have been overcome during the time by combining it with other interpolation operators or by modifying the basis functions. One way to improve the method is described by A. V. Masjukov and V. V. Masjukov in [11] and consists of constructing an iterative multiscale method. This idea has been used by other authors in order to obtain better approximation results (see, e.g., [5]).

The modified Shepard operator introduced by Franke and Nielson in [10] and later on improved in [9], [14], [15] requires some artificial parameters such as a number of closest nodes or a radius of influence. The iterative method [11] is free of these setup parameters and performs at each iteration a reduction of the current interpolation result’s residue. The accuracy of this method is comparable to the modified Shepard procedure as shown in [11], although for both methods there are cases when one is preferred to the other.

Consider $f:X\subset\mathbb{R}^{2}\to\mathbb{R}$ and the distinct nodes $(x_{i},y_{i})\in X,\;i=1,...,N$ . Denoting by $d_{i}\left(x,y\right)$ the distance between a given point $\left(x,y\right)\in X$ and the node $\left(x_{i},y_{i}\right),\;i=1,...,N$ , the Shepard operator in the bivariate case is defined as

\left(S^{\mu}f\right)\left(x,y\right)={\sum\limits_{i=1}^{N}}A_{i,\mu}\left(x,% y\right)f\left(x_{i},y_{i}\right),

where

A_{i,\mu}\left(x,y\right)=\frac{{\textstyle\prod\limits_{\begin{subarray}{c}j=% 1\\ j\neq i\end{subarray}}^{N}}d_{j}^{\mu}\left(x,y\right)}{{\textstyle\sum\limits% _{k=1}^{N}}{\textstyle\prod\limits_{\begin{subarray}{c}j=1\\ j\neq k\end{subarray}}^{N}}d_{j}^{\mu}\left(x,y\right)},

(1)

with the parameter $\mu>0$ , whose choice could change the behaviour of the operator.

It is well-known that method’s accuracy can be improved by considering the modified Shepard operator, defined as:

\left(S^{w}f\right)\left(x,y\right)=\frac{{{\textstyle\sum\limits_{i=1}^{N}}}W% _{i}\left(x,y\right)f\left(x_{i},y_{i}\right)}{{{\textstyle\sum\limits_{i=1}^{% N}}}W_{i}\left(x,y\right)},

with

W_{i}\left(x,y\right)=\left[\tfrac{(R^{w}-d_{i})_{+}}{R^{w}d_{i}}\right]^{2},

(2)

where

u_{+}=\left\{\begin{array}[]{ll}u,&\mbox{if }u>0,\\ 0,&\mbox{otherwise},\end{array}\right.

and $R^{w}$ is a radius of influence about the node $(x_{i},y_{i})$ which depends on $i$ . It is computed as the distance between the node $i$ and the $n$ th nearest node to it for $n>N_{w}$ , where $N_{w}$ is fixed. In addition, $n$ should be as small as possible within the constraint that the $n$ th nearest node is significantly more distant than the $(n-1)$ st nearest node (see, e.g., [15]).

Starting with Shepard himself, many other authors have proposed to apply the operator not on $f(x_{i},y_{i})$ directly, but on some interpolation operator $P(f)(x_{i},y_{i})$ in order to obtain better results. So, the combined Shepard operator is given by

\left(S^{\mu}_{P}f\right)\left(x,y\right)={\sum\limits_{i=1}^{N}}A_{i,\mu}% \left(x,y\right)P(f)\left(x_{i},y_{i}\right),

with $A_{i,\mu}$ defined in (1) and $\mu>0$ .

Many operators have been constructed in this way (see, e.g., [1]-[4], [7], [8]).

Based on the least squares thin-plate spline type function, the classical and the modified Shepard operators, it is introduced in [6] the Shepard operator of least squares thin-plate spline type. An improvement of the method is obtained by replacing the initial set of nodes with a representative smaller set of knot points, using an idea described by McMahon and Franke in [12] and [13].

2 The Iterative Shepard operator of least squares thin-plate spline type

Consider $f:X\subset\mathbb{R}^{2}\to\mathbb{R}$ and the distinct nodes $(x_{i},y_{i})\in X,\;i=1,...,N$ . The classical Shepard operator combined with a least squares thin-plate spline is defined in [6] as

(S_{1}f)(x,y)={\sum\limits_{i=1}^{N}}A_{i,\mu}(x,y)F_{i}(x,y),

(3)

where $A_{i,\mu},$ $i=1,...,N,$ are defined by (1), for a given parameter $\mu>0$ .

The modified Shepard operator of least squares thin-plate spline type has the form

(S_{2}f)(x,y)=\frac{{\sum\limits_{i=1}^{N}}W_{i}\left(x,y\right)F_{i}(x,y)}{{% \sum\limits_{i=1}^{N}}W_{i}\left(x,y\right)},

(4)

where $W_{i},\;i=1,...,N,$ are defined by (2).

In both cases the least squares thin-plate spline $F_{i},\;i=1,...,N$ , is given by

F_{i}(x,y)={\textstyle\sum\limits_{j=1}^{i}}C_{j}d_{j}^{2}\log(d_{j})+ax+by+c,

(5)

with $d_{j}=\sqrt{(x-x_{j})^{2}+(y-y_{j})^{2}}.$

The coefficients $C_{j},$ $a,$ $b,$ $c$ are found in order to minimize the expression (see, e.g., [6], [12]):

E={\textstyle\sum\limits_{i=1}^{N}}[F_{i}(x_{i},y_{i})-f(x_{i},y_{i})]^{2},

by solving a system that has the form

\begin{pmatrix}M&X\\ X^{T}&O_{3}\end{pmatrix}\cdot\begin{pmatrix}\bm{C}\\ \mathbf{v}\end{pmatrix}=\begin{pmatrix}\mathbf{f}\\ \mathbf{0}\end{pmatrix},

considering the following notations:

•

$M=\left(m_{ij}\right)_{i,j=\overline{1,N}}$ , $m_{ij}=\left\{\begin{array}[]{cc}d_{ij}^{2}\log(d_{ij}),&\;\;i\neq j\\ 0,&\;\;i=j\end{array}\right.$ , with $d_{ij}=\sqrt{(x_{i}-x_{j})^{2}+(y_{i}-y_{j})^{2}}$ ;
•

$\mathbf{X}=\begin{pmatrix}x_{1}&y_{1}&1\\ \vdots&\vdots&\vdots\\ x_{N}&y_{N}&1\\ \end{pmatrix}$ ;
•

$C=\left(C_{1},...,C_{N}\right)^{T}$ , $\mathbf{v}=(a,b,c)^{T}$ , $\mathbf{f}=(f_{1},...,f_{N})^{T}$ and $\mathbf{0}=(0,0,0)^{T}$ .

To improve method’s results, the initial set of $N$ nodes has been replaced by a smaller subset of $k$ representative knot points $(x_{i},y_{i}),\;i=1,...,k$ , following an idea from [12]. The algorithm is also described in [6]. In short, using a randomly generated set of knot points, the procedure consists in replacing the set of knot points by the centroids of each subset of points that are closest to the same knot, until the set of knots has not changed for two consecutive iterations. Using these knot points, the classical Shepard operator and the modified Shepard operator are defined in a similar way.

The iterative Shepard operator introduced in [11] is of the following form

u(x,y)=\sum\limits_{k=0}^{K}\sum\limits_{j=1}^{N^{\prime}}\left[u_{j}^{(k)}w% \left((x-x_{j},y-y_{j})/\tau_{k}\right)/\sum\limits_{p=1}^{N^{\prime}}w\left((% x_{p}-x_{j},y_{p}-y_{j})/\tau_{k}\right)\right],

(6)

with $(x,y)\in X,\;(x_{i},y_{i})\in X,\;i=1,...,N^{\prime}$ , are the interpolation nodes and $w$ is a continuously differentiable weight function, having the properties that

w(x,y)\geq 0,\;\forall(x,y)\in\mathbb{R}^{2},\;w(0,0)>0\mbox{ and }w(x,y)=0% \mbox{ if }\|(x,y)\|>1.

$u_{j}^{(k)}$ denotes the interpolation residuals at the $k$ th step, with $u_{j}^{(0)}\equiv u_{j}$ .

Keeping the ideas from [11] and based on the method described in the paper, we define the iterative Shepard operator of least squares thin-plate spline type, denoted by $u_{L}$ , as

u_{L}(x,y)=\sum\limits_{k=0}^{K}\sum\limits_{j=1}^{N^{\prime}}\left[u_{F_{j}}^% {(k)}w\left((x-x_{j},y-y_{j})/\tau_{k}\right)/\sum\limits_{p=1}^{N^{\prime}}w% \left((x_{p}-x_{j},y_{p}-y_{j})/\tau_{k}\right)\right],

(7)

where $(x,y)\in X,\;(x_{i},y_{i})\in X,\;i=1,...,N^{\prime}$ , and the interpolation residuals at the $k$ th step $u_{F_{j}}^{(k)}$ are given by

u_{F_{j}}^{(0)}=F_{j}(x_{j},y_{j}),\;(x_{j},y_{j})\in X,\;j=1,...,N^{\prime}

and

u_{F_{j}}^{(k+1)}=u_{F_{j}}^{(k)}-\sum\limits_{q=1}^{N^{\prime}}\left[u_{F_{q}% }^{(k)}w\left((x_{j}-x_{q},y_{j}-y_{q})/\tau_{k}\right)/\sum\limits_{p=1}^{N^{% \prime}}w\left((x_{p}-x_{q},y_{p}-y_{q})/\tau_{k}\right)\right].

The functions $F_{i}$ are the least squares thin-plate splines, given in (5). The parameter $\tau_{k}$ is chosen as in [11] and it decreases from a given value $\tau_{0}$ , which can be, for example

\tau_{0}>\sup\limits_{(x,y)\in X}\max\limits_{1\leq j\leq N^{\prime}}\|(x-x_{j% },y-y_{j})\|

\tau_{K}<\min\limits_{i\neq j}\|(x_{i}-x_{j},y_{i}-y_{j})\|.

The sequence $\{\tau_{k}\}$ of scale factors is given by

\tau_{k}=\gamma^{k}\tau_{0},\;\;\;\;\;\gamma\in(0,1).

It was also shown in [11] that by applying the idea of multiscale analysis, the behaviour of the interpolant does not change very much for values of $\gamma$ from $0.6$ to $0.95$ . Smaller values of $\gamma$ could also be chosen for decreased computational time, in the case of sparsed interpolation nodes.

The weight function $w$ is defined as

w(x,y)=w(x)w(y)

with

w(x)=\left\{\begin{array}[]{ll}5(1-|x|)^{4}-4(1-|x|)^{5},&|x|<1\\ 0,&|x|\geq 1\end{array}.\right.

We construct the iterative Shepard operator of least squares thin-plate spline type on both sets of interpolation nodes that were mentioned before: firstly for $N^{\prime}=N$ nodes and then for $N^{\prime}=k$ knot points that are representative for the initial set of $N$ nodes, with $k<N$ .

3 Test results

We consider the following test functions (see, e.g., [9], [14], [15]):

\begin{array}[c]{ll}\text{Gentle:}&f_{1}(x,y)=\exp[-\tfrac{81}{16}((x-0.5)^{2}% +(y-0.5)^{2})]/3,\\ \text{Saddle:}&f_{2}(x,y)=\dfrac{(1.25+\cos 5.4y)}{6+6(3x-1)^{2}}.\end{array}

(8)

Table 1 contains the maximum errors for approximating the functions given in (8) by the corresponding two iterative Shepard operators given in (7), for N=100 random generated points in $[0,1]\times[0,1]$ and k=25 knot points. We consider $\tau_{0}=3$ , $K=20$ and $\gamma=0.66,\;0.84$ . We also compute the maximum errors for the classical and the modified Shepard operators of least squares type given in (3) and (4), respectively. We consider both sets of nodes, the 100 initial interpolation nodes and the 25 representative knot points, for $\mu=3$ and $N_{w}=19$ .

In Figures 1 - 2 we plot the graphs of $f_{1},\;f_{2}$ and the corresponding iterative Shepard operator $u_{L}$ when $N^{\prime}=N=100$ and $N^{\prime}=k=25$ .

We observe that in all the cases, the choice of the 25 representative knot points produces better approximation results, this illustrating the benefits of the algorithm of choosing the representative set of knot points. Also, the smallest error for the approximation of the Saddle function is attained using the iterative Shepard operator of least squares type and for the approximation of the Gentle function is obtained for the modified Shepard operator of least squares type. Because the differences are not large, the two methods are comparable, depending on the set of data that is used, both of them having important advantages, as previously mentioned.

Table 1: Maximum approximation errors.

		$f_{1}$	$f_{2}$
$u_{L}$ , $\gamma=0.66$	$k=25$	0.1635	0.2166
$u_{L}$ , $\gamma=0.66$	$N=100$	0.1693	0.2496
$u_{L}$ , $\gamma=0.84$	$k=25$	0.1336	0.2176
$u_{L}$ , $\gamma=0.84$	$N=100$	0.1603	0.2233
$S_{1}f$	$k=25$	0.1578	0.3783
$S_{1}f$	$N=100$	0.1644	0.4001
$S_{2}f$	$k=25$	0.1212	0.2834
$S_{2}f$	$N=100$	0.1246	0.2858

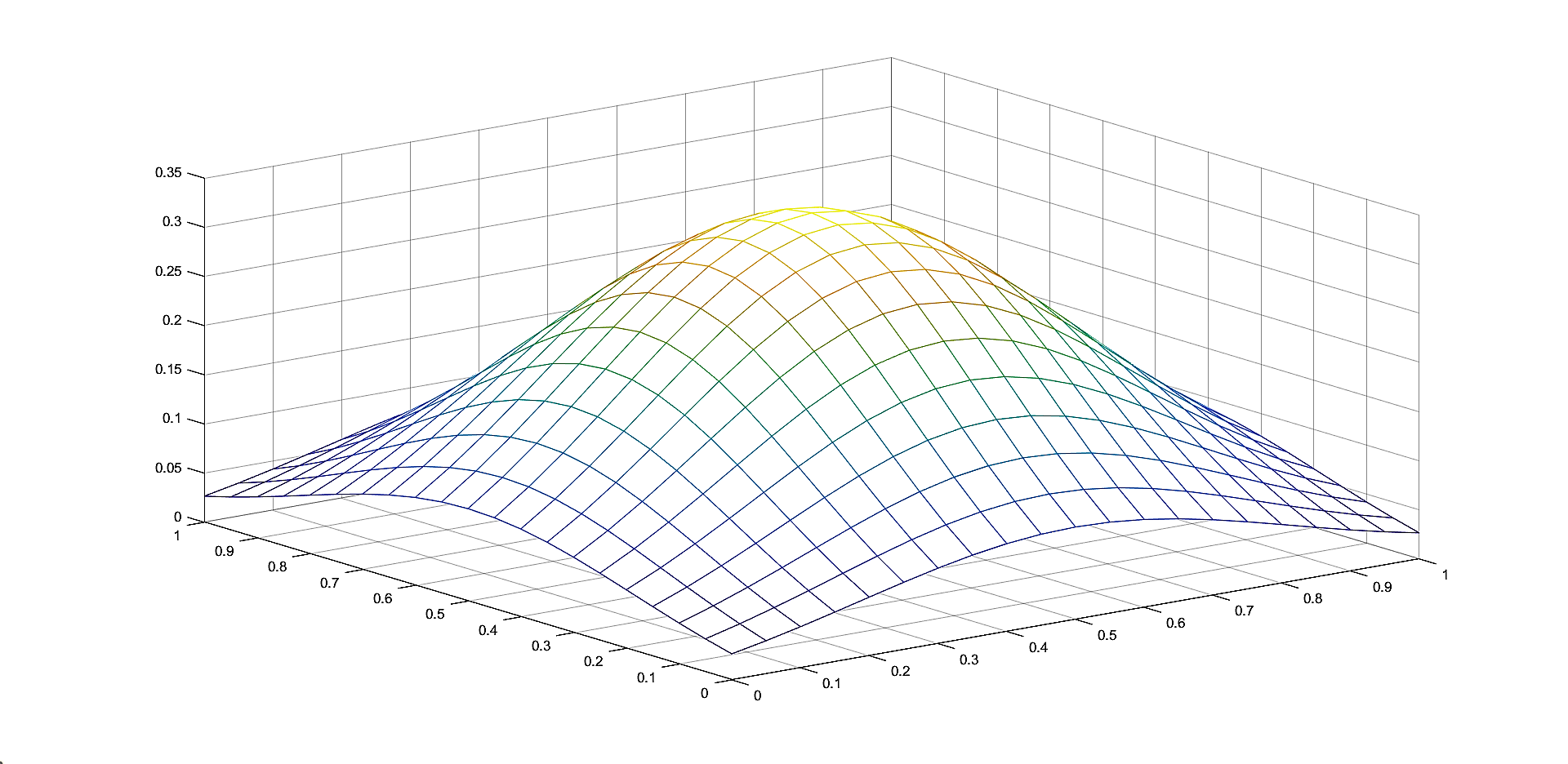
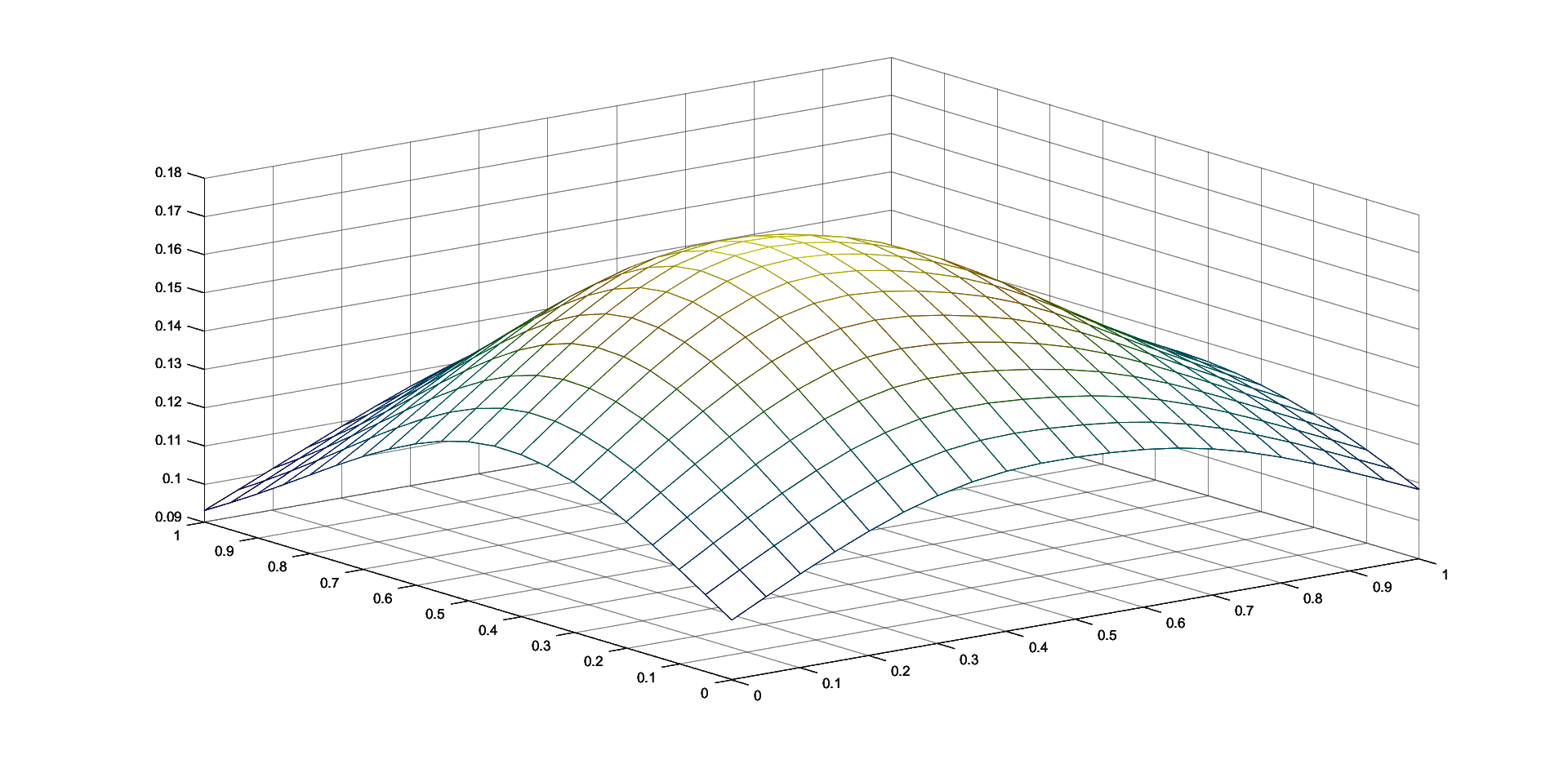
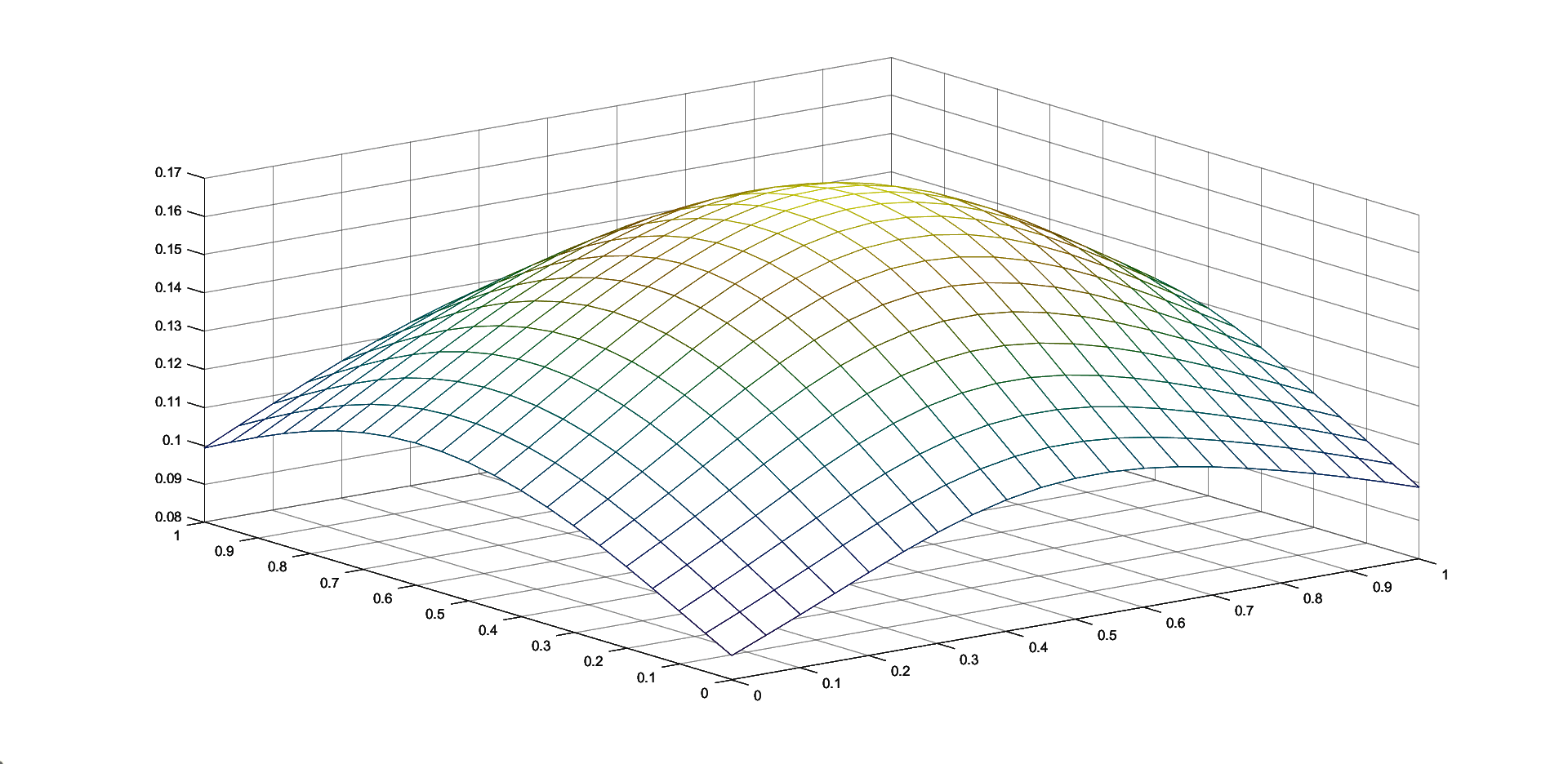
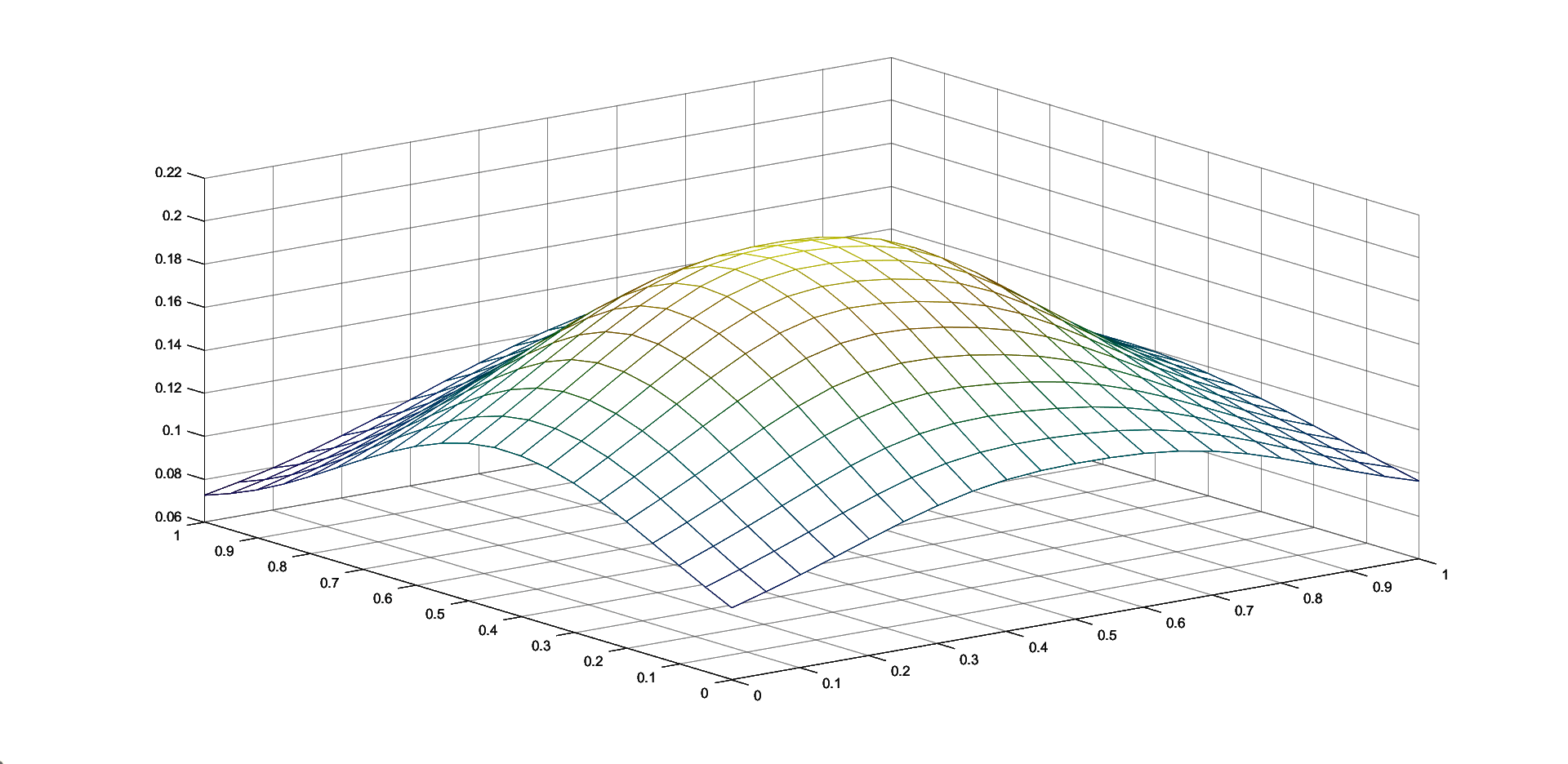
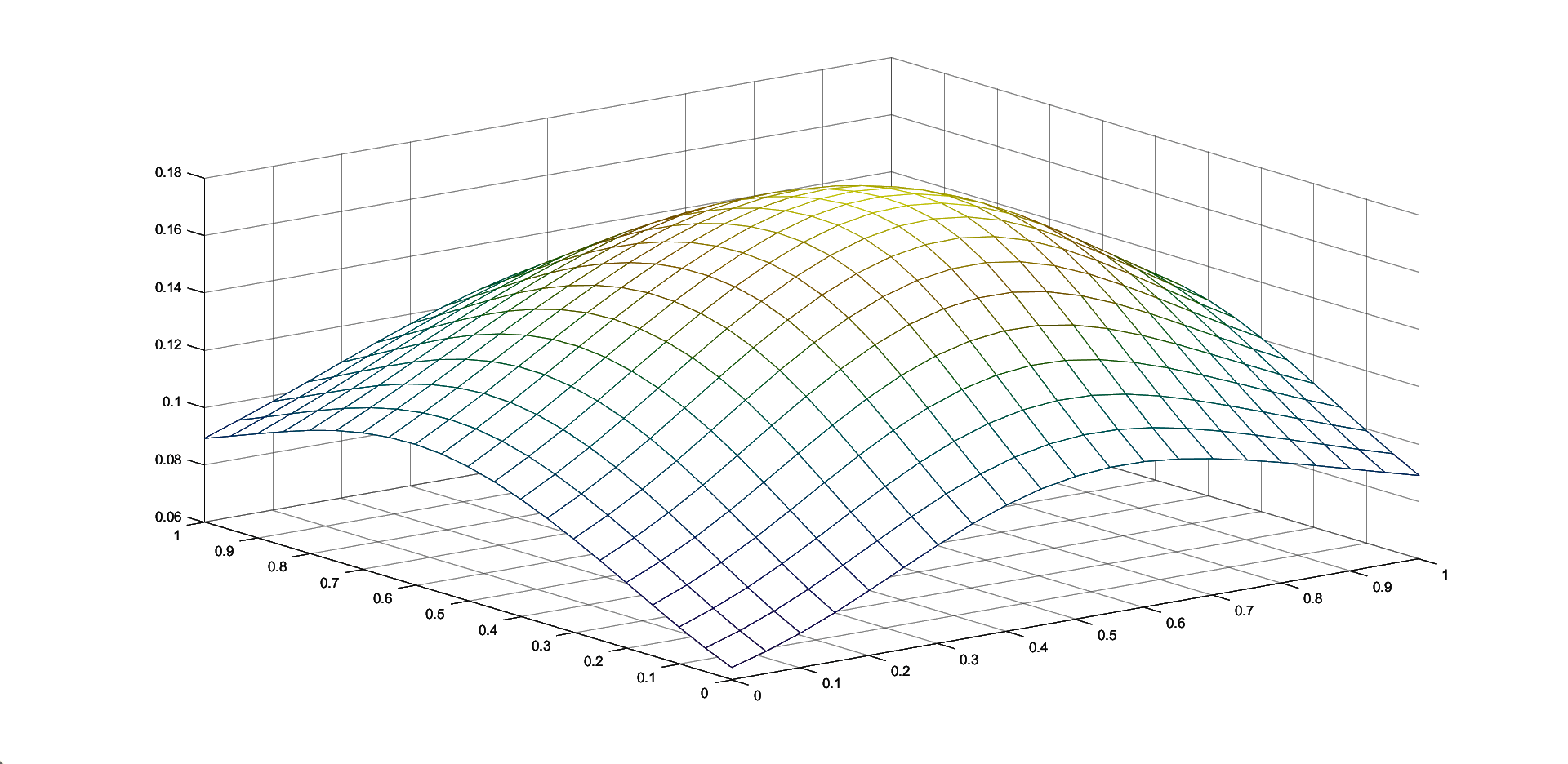
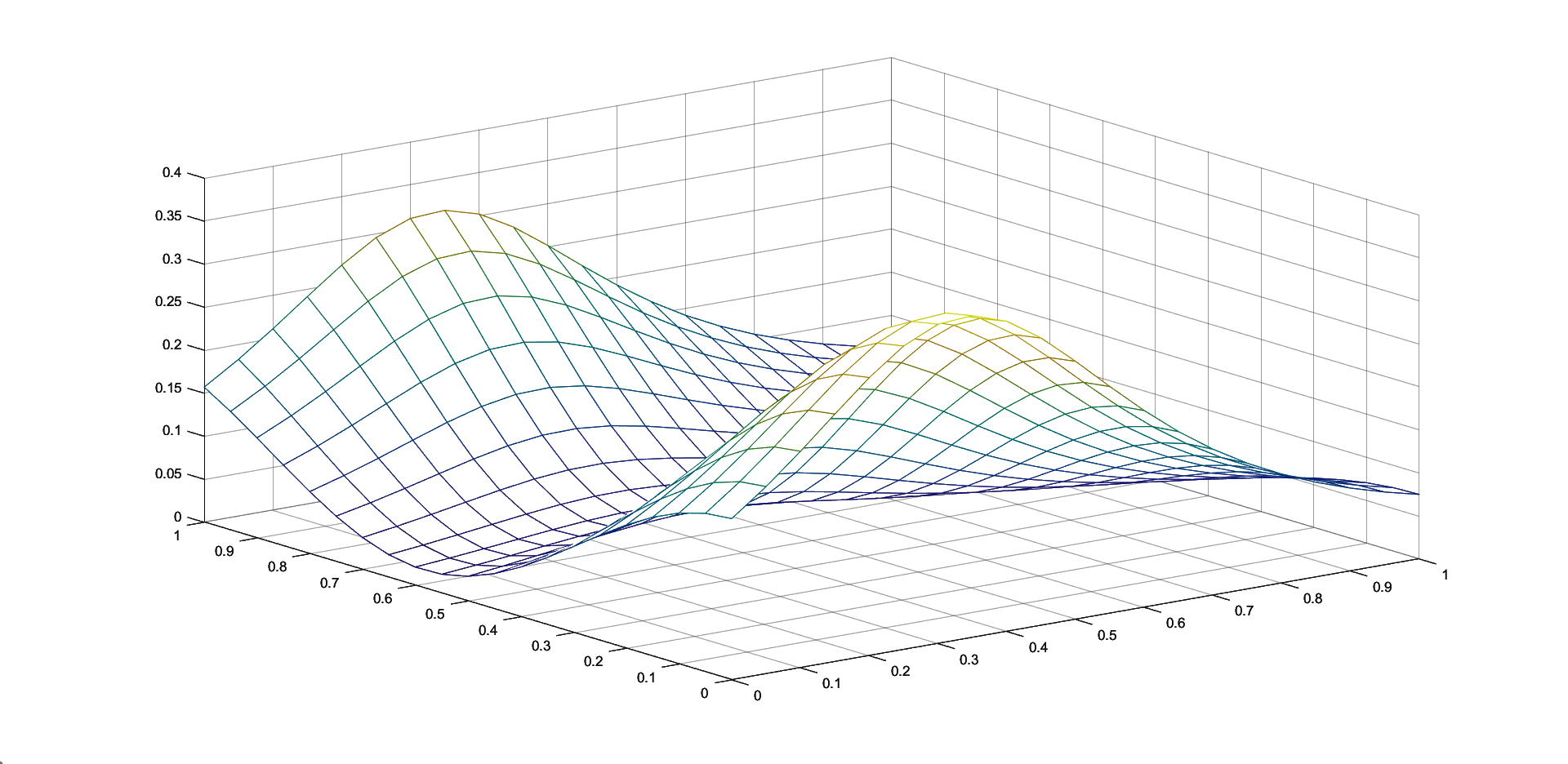
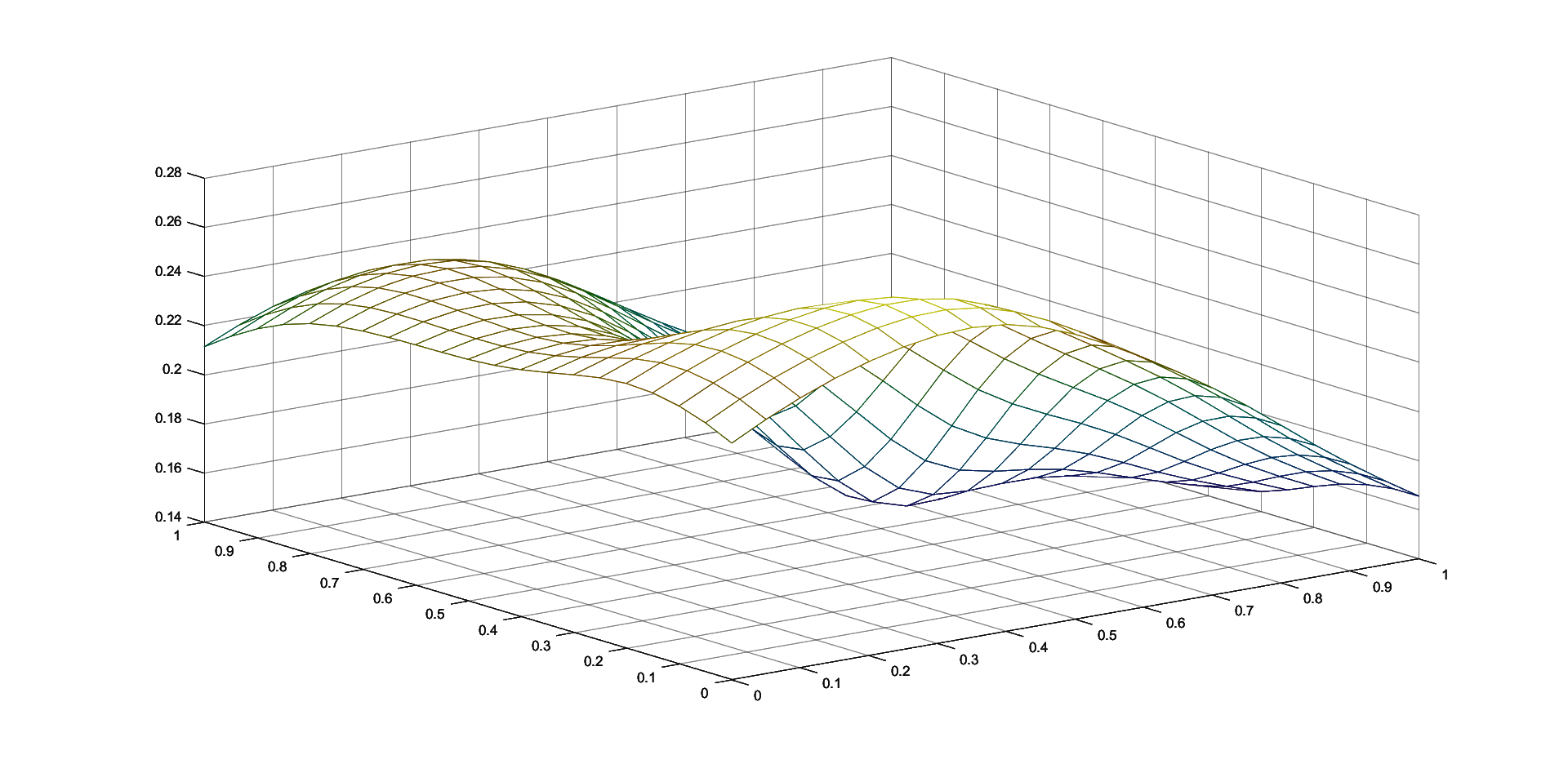
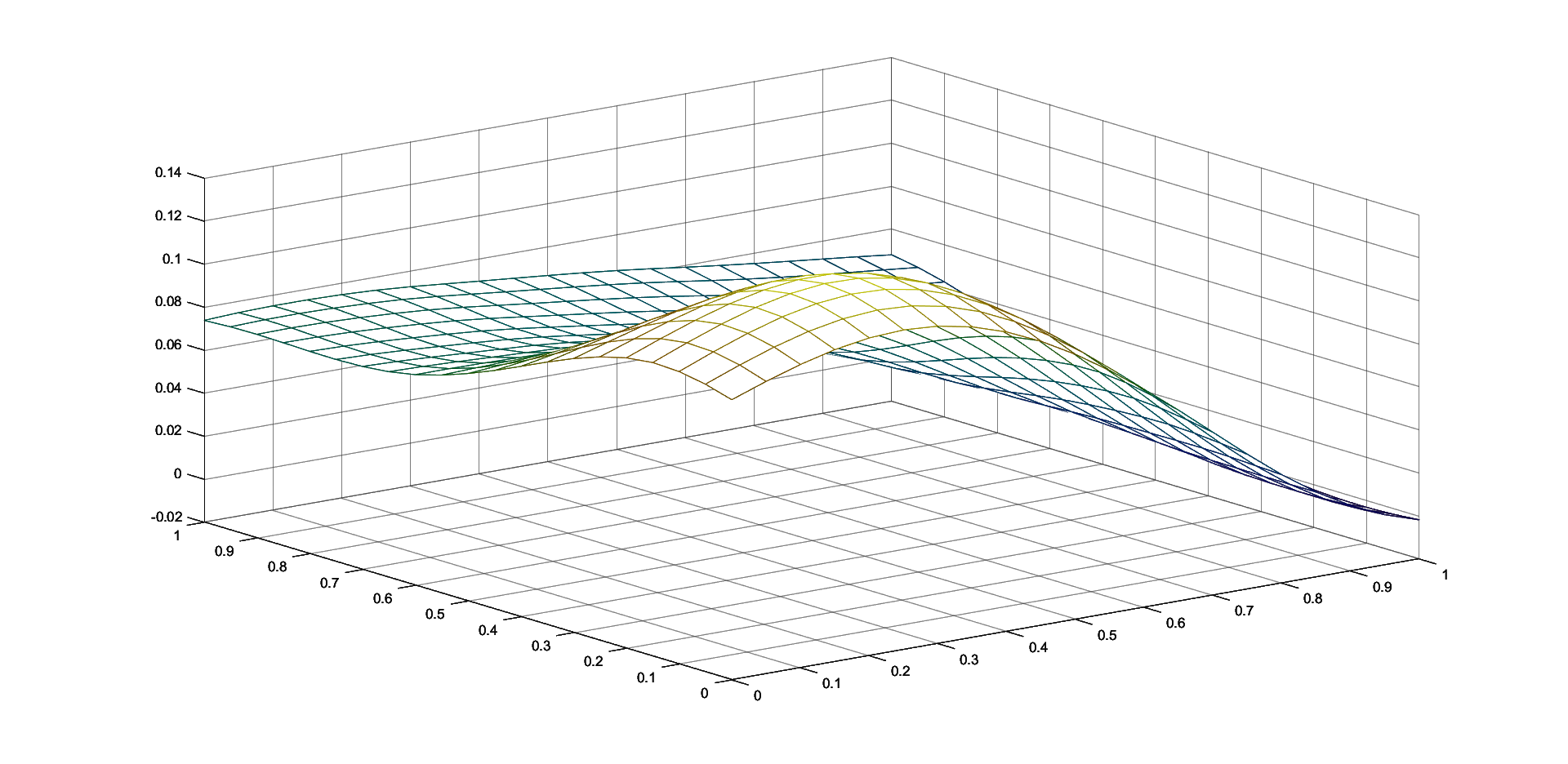
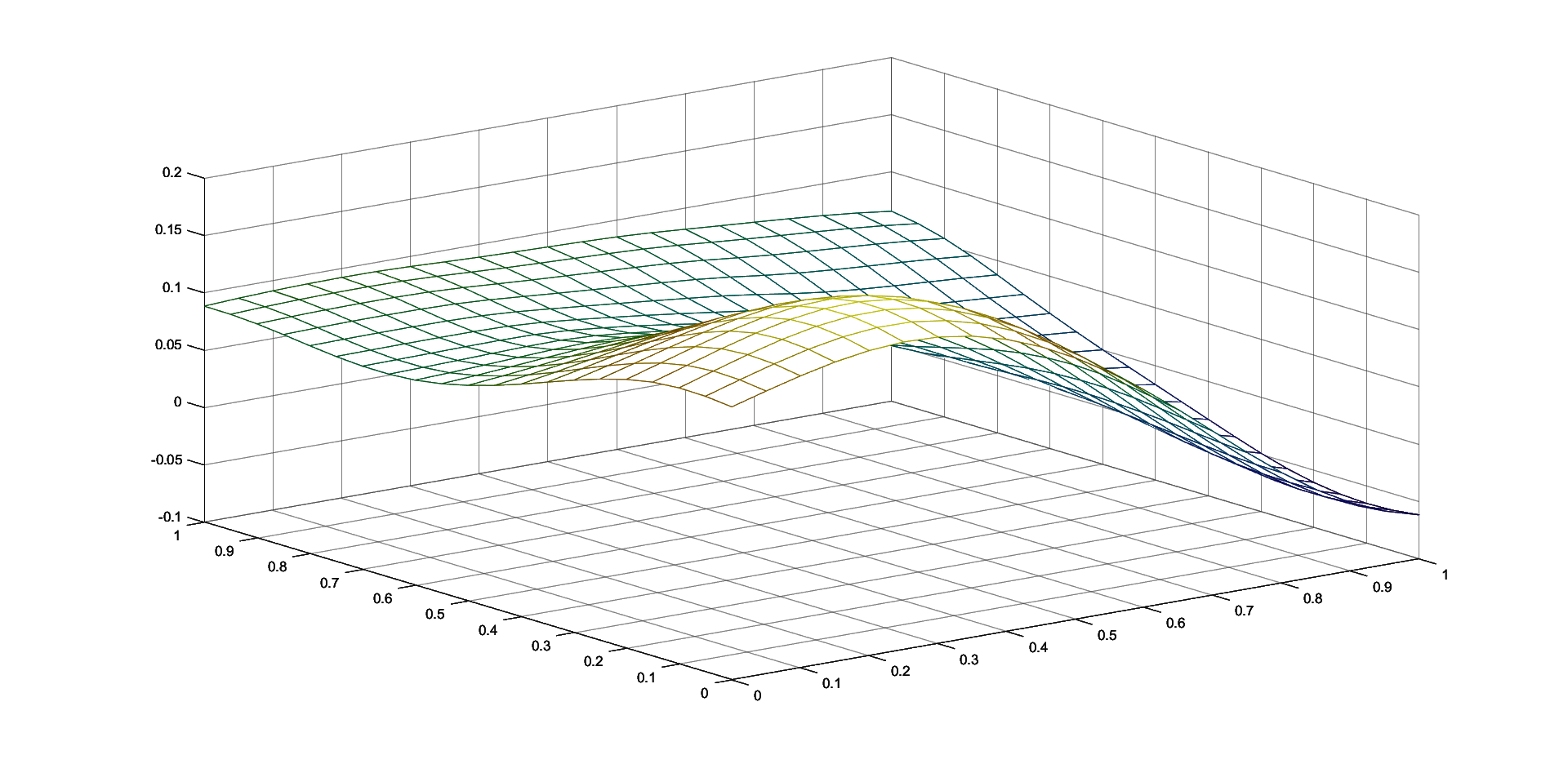
4 Conclusions

In this paper we have proposed an iterative modification of the Shepard operator of least squares thin-plate spline type, introduced in [6]. For the given sets of interpolation nodes, smaller subsets of representative knot points are constructed and the numerical results demonstrate the benefits of this algorithm. The advantages of this method are also confirmed by the numerical results.

References

[1] T. Cătinaş. The combined Shepard-Abel-Goncharov univariate operator. Rev. Anal. Numér. Théor. Approx., 32:11–20, 2003.
[2] T. Cătinaş. The combined Shepard-Lidstone bivariate operator. In: de Bruin, M.G. et al. (eds.): Trends and Applications in Constructive Approximation. International Series of Numerical Mathematics, Springer Group-Birkhäuser Verlag, 151:77–89, 2005.
[3] T. Cătinaş. Bivariate interpolation by combined Shepard operators. Proceedings of $17^{th}$ IMACS World Congress, Scientific Computation, Applied Mathematics and Simulation, 7pp., 2005.
[4] T. Cătinaş. The bivariate Shepard operator of Bernoulli type. Calcolo, 44(4):189–202, 2007.
[5] T. Cătinaş. An iterative modification of Shepard-Bernoulli Operator. Results Math., 69:387–395, 2016.
[6] T. Cătinaş, A. Malina. Shepard operator of least squares thin-plate spline type. Stud. Univ. Babeş-Bolyai Math. 66(2):257–265, 2021.
[7] Gh. Coman. Hermite-type Shepard operators. Rev. Anal. Numér. Théor. Approx., 26:33–38, 1997.
[8] Gh. Coman. Shepard operators of Birkhoff type. Calcolo, 35:197–203, 1998.
[9] R. Franke. Scattered data interpolation: tests of some methods. Math. Comp., 38:181–200, 1982.
[10] R. Franke, G. Nielson. Smooth interpolation of large sets of scattered data. Int. J. Numer. Meths. Engrg. 15:1691–1704, 1980.
[11] A.V. Masjukov, V.V. Masjukov. Multiscale modification of Shepard’s method for interpolation of multivariate scattered data. Mathematical Modelling and Analysis, Proceeding of the 10th International Conference MMA2005 & CMAM2, 467-472.
[12] J.R. McMahon. Knot selection for least squares approximation using thin plate splines. M.S. Thesis, Naval Postgraduate School, 1986.
[13] J.R. McMahon, R. Franke. Knot selection for least squares thin plate splines. Technical Report, Naval Postgraduate School, Monterey, 1987.
[14] R.J. Renka, A.K. Cline. A triangle-based $C^{1}$ interpolation method. Rocky Mountain J. Math., 14:223–237, 1984.
[15] R.J. Renka. Multivariate interpolation of large sets of scattered data. ACM Trans. Math. Software, 14:139–148, 1988.
[16] D. Shepard. A two dimensional interpolation function for irregularly spaced data. Proceedings of the 23rd ACM National Conference, New York: ACM Press, 517–523, 1968.

Iterative Shepard operator of least squares thin-plate spline type

Abstract

Authors

Keywords

Paper coordinates

PDF

About this paper

Journal

Publisher Name

DOI

Online ISSN

Paper (preprint) in HTML form

Iterative Shepard operator of least squares thin-plate spline type

Abstract

1 Preliminaries

2 The Iterative Shepard operator of least squares thin-plate spline type

3 Test results

4 Conclusions

References

References

Related Posts