The combined Shepard operator of inverse quadratic and inverse multiquadric type

Andra Malina
approximation of multivariate functions, Approximation Theory, not-at-ICTP, Shepard

Abstract

Starting with the classical, the modified and the iterative Shepard methods, we construct some new Shepard type operators, using the inverse quadratic and the inverse multiquadric radial basis functions. Given some sets of points, we compute some representative subsets of knot points following an algorithm described by J.R. McMahon in 1986.

Authors

Teodora Catinas
Babes-Bolyai University, Faculty of Mathematics and Computer Sciences
Babes-Bolyai University, Faculty of Mathematics and Computer Sciences
Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy

Keywords

Shepard operator; inverse quadratic; inverse multiquadric; knot points.

Paper coordinates

T. Cătinaș, A. Malina, The combined Shepard operator of inverse quadratic and inverse multiquadric type, Stud. Univ. Babeș-Bolyai Math., 67(2022), No. 3, pp. 579-589.

doi: http://doi.org/10.24193/subbmath.2022.3.09

PDF

http://www.cs.ubbcluj.ro/~studia-m/index.php/journal/article/view/1486

About this paper

Journal

Studia

Publisher Name

Univ. Babes-Bolyai Math.

DOI

10.24193/subbmath.2022.3.09

Print ISSN

0252-1938

Online ISSN

2065-961x

Google Scholar Profile

https://scholar.google.com/citations?user=_yNNgu4AAAAJ&hl=ro

Paper (preprint) in HTML form

The combined Shepard operator of inverse quadratic and inverse multiquadric type: The combined Shepard operator of inverse quadratic and inverse multiquadric type

The combined Shepard operator of inverse quadratic and inverse multiquadric type

Teodora Cătinaş\(^{*}\), Andra Malina\(^{*}\)

\(^{*}\)"Babeş-Bolyai" University, Faculty of Mathematics and Computer Sciences 1, Kogălniceanu Street, 400084 Cluj-Napoca, Romania
e-mail: tcatinas@math.ubbcluj.ro, andra.malina@ubbcluj.ro

MSC. 41A05, 41A25, 41A80.
Keywords. Shepard operator, inverse quadratic, inverse multiquadric, knot points.
Abstract. Starting with the classical, the modified and the iterative Shepard methods, we construct some new Shepard type operators, using the inverse quadratic and the inverse multiquadric radial basis functions. Given some sets of points, we compute some representative subsets of knot points following an algorithm described by J. R. McMahon in 1986.

1 Preliminaries

Over the time Shepard method, introduced in 1968 in [ 21 ] , has been improved in order to get better reproduction qualities, higher accuracy and lower computational cost (see, e.g., [ 2 ] - [ 9 ] , [ 22 ] , [ 23 ] ).

Let \(f\) be a real-valued function defined on \(X\subset \mathbb {R}^{2},\) and \((x_{i},y_{i})\in X,\; \\ i=1,...,N\) some distinct points. The bivariate Shepard operator is defined by

\begin{equation} \left( S_{\mu }f\right) \left( x,y\right) ={\sum \limits _{i=1}^{N}}A_{i,\mu }\left( x,y\right) f\left( x_{i},y_{i}\right) , \label{clasic} \end{equation}
1.1

where

\begin{equation} A_{i,\mu }\left( x,y\right) =\frac{{\textstyle \prod \limits _{\substack {j=1\\ j\neq i}}^{N}}r_{j}^{\mu }\left( x,y\right) }{{\textstyle \sum \limits _{k=1}^{N}}{\textstyle \prod \limits _{\substack {j=1\\ j\neq k}}^{N}}r_{j}^{\mu }\left( x,y\right) }, \label{ai}\end{equation}
1.2

with the parameter \(\mu {\gt}0\) and \(r_{i}\left( x,y\right) \) denoting the distances between a given point \(\left( x,y\right) \in X\) and the points \(\left( x_{i},y_{i}\right) ,\; i=1,...,N\).

In [ 11 ] , Franke and Nielson introduced a method for improving the accuracy in reproducing a surface with the bivariate Shepard approximation. This method has been further improved in [ 10 ] , [ 19 ] , [ 20 ] , and it is given by:

\begin{equation} \left( Sf\right) \left( x,y\right) =\frac{{{\textstyle \sum \limits _{i=1}^{N}} }W_{i}\left( x,y\right) f\left( x_{i},y_{i}\right) }{{{\textstyle \sum \limits _{i=1}^{N}} }W_{i}\left( x,y\right) },\label{Shimproved} \end{equation}
1.3

with

\begin{equation} W_{i}\left( x,y\right) =\left[ \tfrac {(R_{w}-r_{i}(x,y))_{+}}{R_{w}r_{i}(x,y)}\right] ^{2},\label{wi} \end{equation}
1.4

where \(R_{w}\) is a radius of influence about the node \((x_{i},y_{i})\) and it is varying with \(i.\) \(R_{w}\) is taken as the distance from node \(i\) to the \(j\)th closest node to \((x_{i},y_{i})\) for \(j{\gt}N_{w}\) (\(N_{w}\) is a fixed value) and \(j\) as small as possible within the constraint that the \(j\)th closest node is significantly more distant than the \((j-1)\)st closest node (see, e.g. [ 20 ] ). As it is mentioned in [ 14 ] , this modified Shepard method is one of the most powerful software tools for the multivariate approximation of large scattered data sets.

A.V. Masjukov and V.V. Masjukov introduced in [ 15 ] an iterative modification for the Shepard operator that requires no artificial parameter, such as a radius of influence or number of nodes. So, they defined the iterative Shepard operator as

\begin{equation} \label{Shiter} u(x,y)=\sum \limits _{k=0}^{K} \sum \limits _{j=1}^{N} \left[ u_{j}^{(k)}w\left((x-x_j,y-y_j)/\tau _k\right) / \sum \limits _{p=1}^{N} w\left((x_p-x_j,y_p-y_j)/ \tau _k\right)\right], \end{equation}
1.5

where \(w\) is the weight function, continuously differentiable, with the properties that

\[ w(x,y) \geq 0,\; \forall (x,y) \in \mathbb {R}^2, \; w(0,0){\gt}0 \mbox{ and } w(x,y)=0 \mbox{ if } \| (x,y)\| {\gt}1, \]

and \(u_j^{(k)}\) denotes the interpolation residuals at the \(k\)th step, with \(u_j^{(0)}\equiv u_j\).

2 The Shepard operators combined with the inverse quadratic and inverse multiquadric radial basis functions

Let \(f\) be a real-valued function defined on \(X\subset \mathbb {R}^{2}.\) We denote by \(\mathbf{x}\) the point \( (x,y) \in X \) and we assume that \(\mathbf{x_i}= (x_i,y_i) \in X,\) \( i = 1,...,N'\), are some given interpolation nodes.

The radial basis functions (RBF) are some modern and very efficient tools for interpolating scattered data, thus they are intensively used (see, e.g., [ 1 ] , [ 12 ] – [ 14 ] , [ 18 ] ). In the sequel we use two radial basis functions that are positive definite, the inverse quadratic RBF and the inverse multiquadric RBF.

Consider the two radial basis functions as

\begin{equation} \label{RBFquadr} \phi _{i}^{\beta }(x,y)= {\textstyle \sum \limits _{j=1}^{i}} \alpha _{j} \left[1+ \left(\epsilon r_j \right) ^2\right]^{\beta }+ax+by+c,\ \ i=1,...,N', \end{equation}
2.1

with \(\epsilon \) being a shape parameter and \(r_j(x,y)=\sqrt{(x-x_{j})^{2}+(y-y_{j})^{2}}.\)

For \(\beta =-1\), \(\mathbf{\phi _i^{-1}}\) is the inverse quadratic RBF and for \(\beta =-1/2\), \(\mathbf{\phi _{i}^{-1/2}}\) is the inverse multiquadric RBF.

The coefficients \(\alpha _j,\; a,\; b,\; c\) are obtained as solutions of systems of the form

\begin{equation*} \begin{pmatrix} 1 & \left[1+ \left(\epsilon r_{12} \right) ^2\right]^{\beta } & \cdots & \left[1+ \left(\epsilon r_{1N'} \right) ^2\right]^{\beta } & x_1 & y_1 & 1 \\ \left[1+ \left(\epsilon r_{21} \right) ^2\right]^{\beta } & 1 & \cdots & \left[1+ \left(\epsilon r_{2N'} \right) ^2\right]^{\beta } & x_2 & y_2 & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \left[1+ \left(\epsilon r_{N'1} \right) ^2\right]^{\beta } & \left[1+ \left(\epsilon r_{N'2} \right) ^2\right]^{\beta } & \cdots & 1 & x_{N'} & y_{N'} & 1 \\ x_1 & x_2 & \cdots & x_{N'} & 0 & 0 & 0 \\ y_1 & y_2 & \cdots & y_{N'} & 0 & 0 & 0 \\ 1 & 1 & \cdots & 1 & 0 & 0 & 0 \\ \end{pmatrix} \cdot \begin{pmatrix} \alpha _1 \\ \alpha _2 \\ \vdots \\ \alpha _{N'} \\ a \\ b \\ c \end{pmatrix} = \begin{pmatrix} f_1 \\ f_2 \\ \vdots \\ f_{N'} \\ 0 \\ 0 \\ 0 \end{pmatrix}\end{equation*}

with \(r_{ij}=\sqrt{(x_i-x_j)^2 + (y_i-y_j)^2}\) and \(f_i=f(\mathbf{x}_i)\).

Shortly, this system can be written as

\begin{equation*} \begin{pmatrix} A & X^T \\ X & O_{3} \end{pmatrix} \cdot \begin{pmatrix} {\alpha } \\ \mathbf{u} \end{pmatrix} = \begin{pmatrix} \mathbf{f} \\ \mathbf{0} \end{pmatrix} , \end{equation*}

considering the following notations:

  • \(A \in \mathcal{M}_{\scriptscriptstyle N' \times N'}(\mathbb {R})\), with the element on the entry \((i, j)\) being
    \(a_{ij} = \left[1+ \left(\epsilon r_{ij} \right) ^2\right]^{\beta }\), where \(r_{ij}=\sqrt{(x_i-x_j)^2 + (y_i-y_j)^2}\),
    \(i, j = 1, ..., N'\) and \(\beta \in \{ -1,\; -1/2\} \);

  • \(X \in \mathcal{M}_{\scriptscriptstyle 3 \times N'}(\mathbb {R}),\; X= \begin{pmatrix} x_{\scriptscriptstyle 1} & ... & x_{\scriptscriptstyle N'} \\ y_{ \scriptscriptstyle 1} & ... & y_{ \scriptscriptstyle N'} \\ 1 & ... & 1 \end{pmatrix}, \) \(O_3\) is the zero square matrix of order 3;

  • \(\mathbf{u} = ( a, \; b, \; c )^{T}\), \( {\alpha }=(\alpha _{\scriptscriptstyle 1}, ..., \alpha _{\scriptscriptstyle N'})^{T}\), \(\mathbf{0} = (0, \; 0, \; 0)^T\) ;

  • \(\mathbf{f} = ( f_{\scriptscriptstyle 1},..., f_{\scriptscriptstyle N'})^{T}\), with \(f_{\scriptscriptstyle i}=f(\mathbf{x}_{\scriptscriptstyle i})\).

First, consider the classical Shepard operator given in (1.1).

Definition 2.1

The classical Shepard operator combined with the inverse quadratic and inverse multiquadric RBF is defined as

\begin{equation} (S_{\mu }^{\beta }f)(\mathbf{x})={\sum \limits _{i=1}^{N'}}A_{i,\mu }(\mathbf{x})\phi _{i}^{\beta }(\mathbf{x}), \label{Sclasic}\end{equation}
2.2

where \(A_{i,\mu },\) \(i=1,...,N',\) are defined by (1.2), for a given parameter \(\mu {\gt}0\) and \(\phi _{i}^{\beta }\) are given in (2.1), for \(\beta \in \{ -1, -1/2\} \) and \(i=1,...,N'\).

Furthermore, we consider the improved form of the Shepard operator, given in (1.3).

Definition 2.2

We define the modified Shepard operator combined with the inverse quadratic and inverse multiquadric RBF as:

\begin{equation} (S_{W}^{\beta }f)(\mathbf{x})=\frac{{\sum \limits _{i=1}^{N'}}W_{i}\left( \mathbf{x}\right) \phi _{i}^{\beta }(\mathbf{x})}{{\sum \limits _{i=1}^{N'}}W_{i}\left( \mathbf{x}\right)},\label{Smodificat}\end{equation}
2.3

with \(W_{i}\), \(i=1,...,N',\) given by (1.4) and \(\phi _{i}^{\beta }\) defined in (2.1), for \(\beta \in \{ -1,-1/2\} \) and \(i=1,...,N'\).

Finally, we follow the idea proposed in [ 15 ] , which consists of using an iterative procedure that requires no artificial parameters.
Definition 2.3

The iterative Shepard operator combined with the inverse quadratic and inverse multiquadric RBF is defined as

\begin{equation} \label{Siterativ} u_{\phi ^{\beta }}(\mathbf{x})=\sum \limits _{k=0}^{K} \sum \limits _{j=1}^{N'} \left[ u_{\phi _{j}^{\beta }}^{(k)}w\left((\mathbf{x-x_j})/\tau _k\right) / \sum \limits _{p=1}^{N'} w\left((\mathbf{x_p-x_j})/ \tau _k \right)\right], \end{equation}
2.4

with \(\beta \in \{ -1, -1/2\} \), where \(u_{\phi _{j}^{\beta }}^{(k)}\) are the interpolation residuals at the \(k\)th step given by

\[ u_{\phi _{j}^{\beta }}^{(0)} = \phi _{j}(\mathbf{x_j}),\; \mathbf{x_j} \in X,\; j=1,...,N' \]

and

\[ u_{\phi _{j}^{\beta }}^{(k+1)}=u_{\phi _{j}^{\beta }}^{(k)} - \sum \limits _{q=1}^{N'} \left[ u_{\phi _{q}^{\beta }}^{(k)}w\left((\mathbf{x_j-x_q})/\tau _k \right) / \sum \limits _{p=1}^{N'} w \left( (\mathbf{x_p-x_q}) / \tau _k \right) \right]. \]

The functions \(\phi _{i}^{\beta }\) are given in (2.1). We follow ideas from [ 15 ] for the parameters’ choice. As an example, the sequence \(\{ \tau _k\} \) of scale factors is defined as

\[ \tau _k = \tau _0 \gamma ^k ,\; \; \; \; \; 0{\lt} \gamma {\lt} 1. \]

The setup parameter \(\tau _k\) can be chosen such that it decreases from an initial value \(\tau _0\), which is given for instance as

\[ \tau _0 {\gt} \sup \limits _{(x,y) \in X} \max \limits _{1 \leq j \leq N'} \| (\mathbf{x-x_j})\| \]

to the final value \(\tau _K\) such that

\[ \tau _K {\lt} \min \limits _{i \neq j} \| (\mathbf{x_i-x_j})\| . \]

The behaviour of \(u_{\phi }^{\beta }\) does not change very much for \(\gamma \) between \(0.6\) and \(0.95\), as shown in [ 15 ] . One can also choose smaller values for \(\gamma \) if the nodes are sparse and a decreased computational time is desired.

Finally, the weight function \(w\) is given by

\[ w(\mathbf{x})=w(x)w(y), \]

with

\[ w(x) = \left\{ \begin{array}{ll} 5(1-|x|)^4 - 4(1-|x|)^5,& |x|{\lt}1 \\ 0, & |x| \geq 1 \end{array}. \right. \]

We apply the three operators on two sets of points. For the first way, we consider a set of \(N\) initial interpolation nodes \(\mathbf{x_i},\; i=1,...,N,\) and for the second way, we consider a smaller set of \(k\in \mathbb {N}^{*}\) knot points \(\mathbf{\hat{x}_{j}},\) \(j=1,...,k\) that will be representative for the original set. This set is obtained following the next steps (see, e.g., [ 16 ] and [ 17 ] ):

Algorithm 2.4

  1. Consider the first subset of \(k\) knot points, \(k {\lt} N\), randomly generated;

  2. Using the Euclidean distance between two points, find the closest knot point for every point;

  3. For the knot points with no point assigned, replace the knot by the nearest point;

  4. Compute the arithmetic mean of all the points that are closest to the same knot and compute in this way the new subset of knot points;

  5. Repeat steps 2-4 until the subset of knot points has not change for two consecutive iterations.

3 Numerical examples

We consider the following test functions (see, e.g., [ 10 ] , [ 19 ] , [ 20 ] ):

\begin{equation} \begin{array}[c]{ll}\text{Gentle:} & f_{1}(x,y)=\exp [-\tfrac {81}{16}((x-0.5)^{2}+(y-0.5)^{2})]/3,\\ \text{Saddle:} & f_{2}(x,y)=\dfrac {(1.25+\cos 5.4y)}{6+6(3x-1)^{2}},\\ \text{Sphere:} & f_{3}(x,y) =\sqrt{64-81((x-0.5)^{2}+(y-0.5)^{2})}/9-0.5. \end{array} \label{fct}\end{equation}
3.1

Tables 1 - 3 contain the maximum errors for approximating the functions (3.1) by the classical, the modified and the iterative Shepard operators given, respectively, by (1.1), (1.3) and (1.5), and the errors of approximating by the operators introduced in (2.2), (2.3) and (2.4). We construct the operators for both radial basis functions - the inverse quadratic and the inverse multiquadric. For each function we consider a set of \(N=100\) random points in \([0,1] \times [0,1]\), a subset of \(k=25\) representative knots, \(\mu = 3\), \(N_w = 19\), \(K=20\), \(\tau _0=3\) and \(\gamma = 0.66,\; 0.84,\; 0.91\).

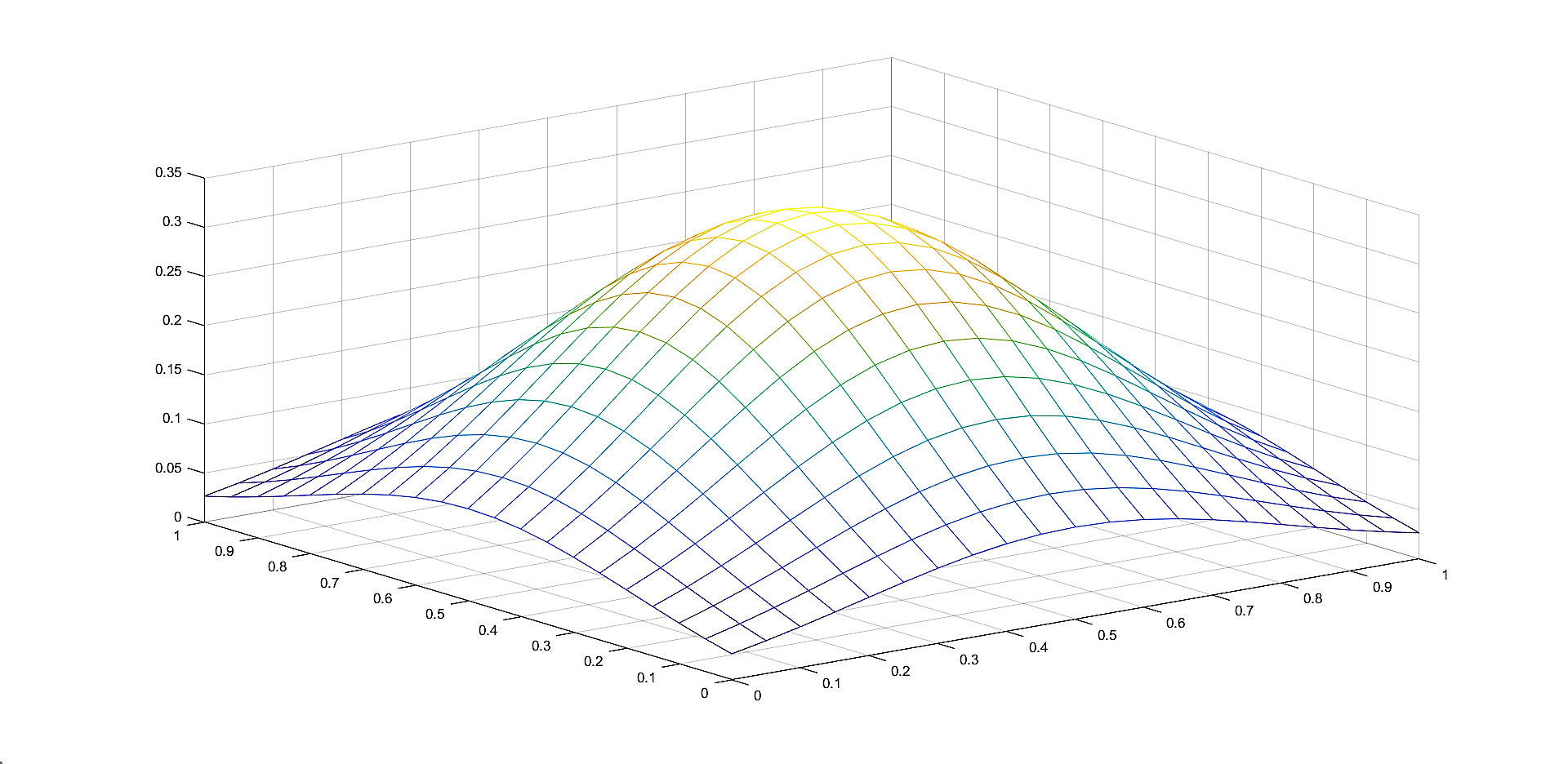
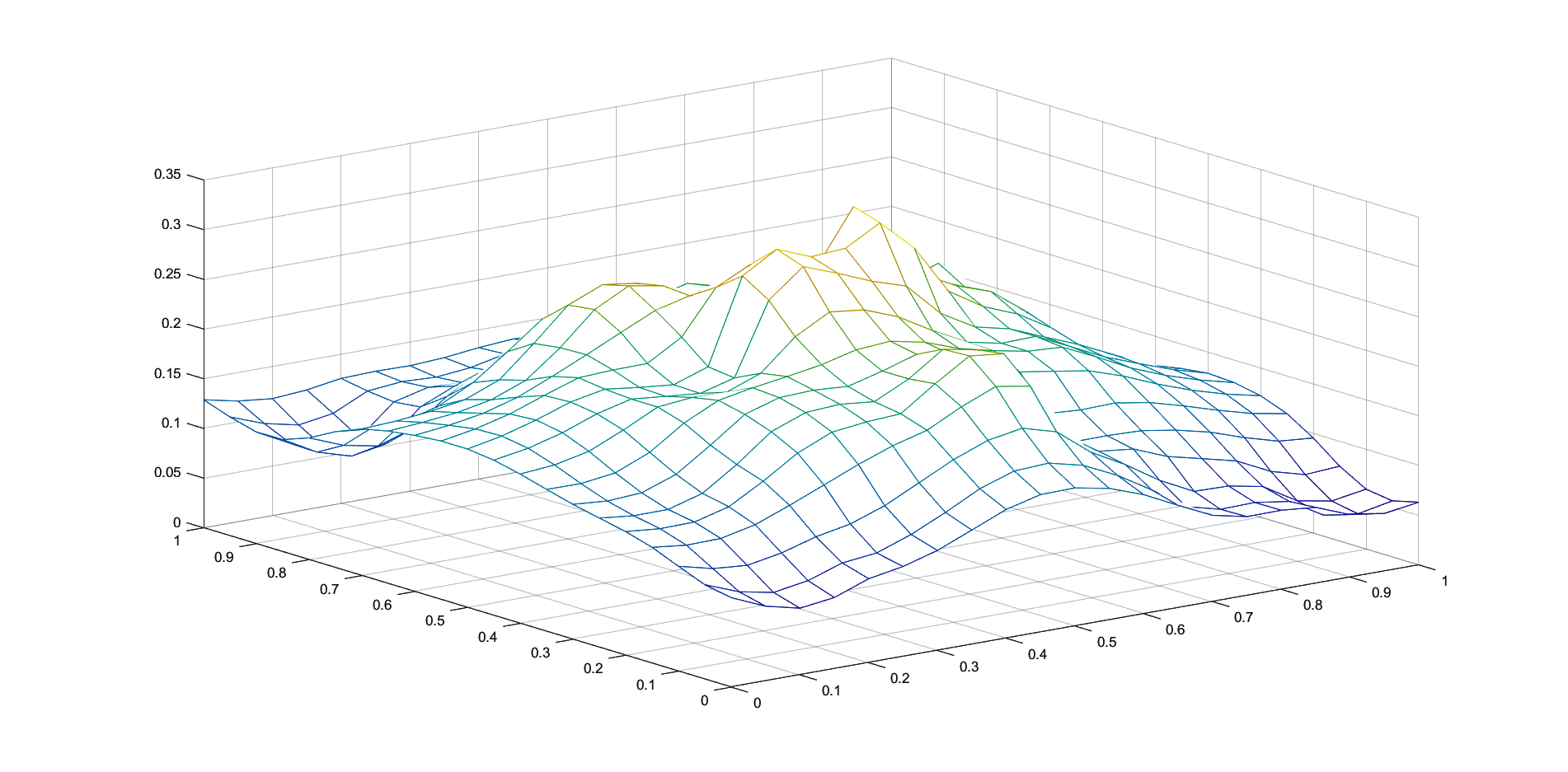
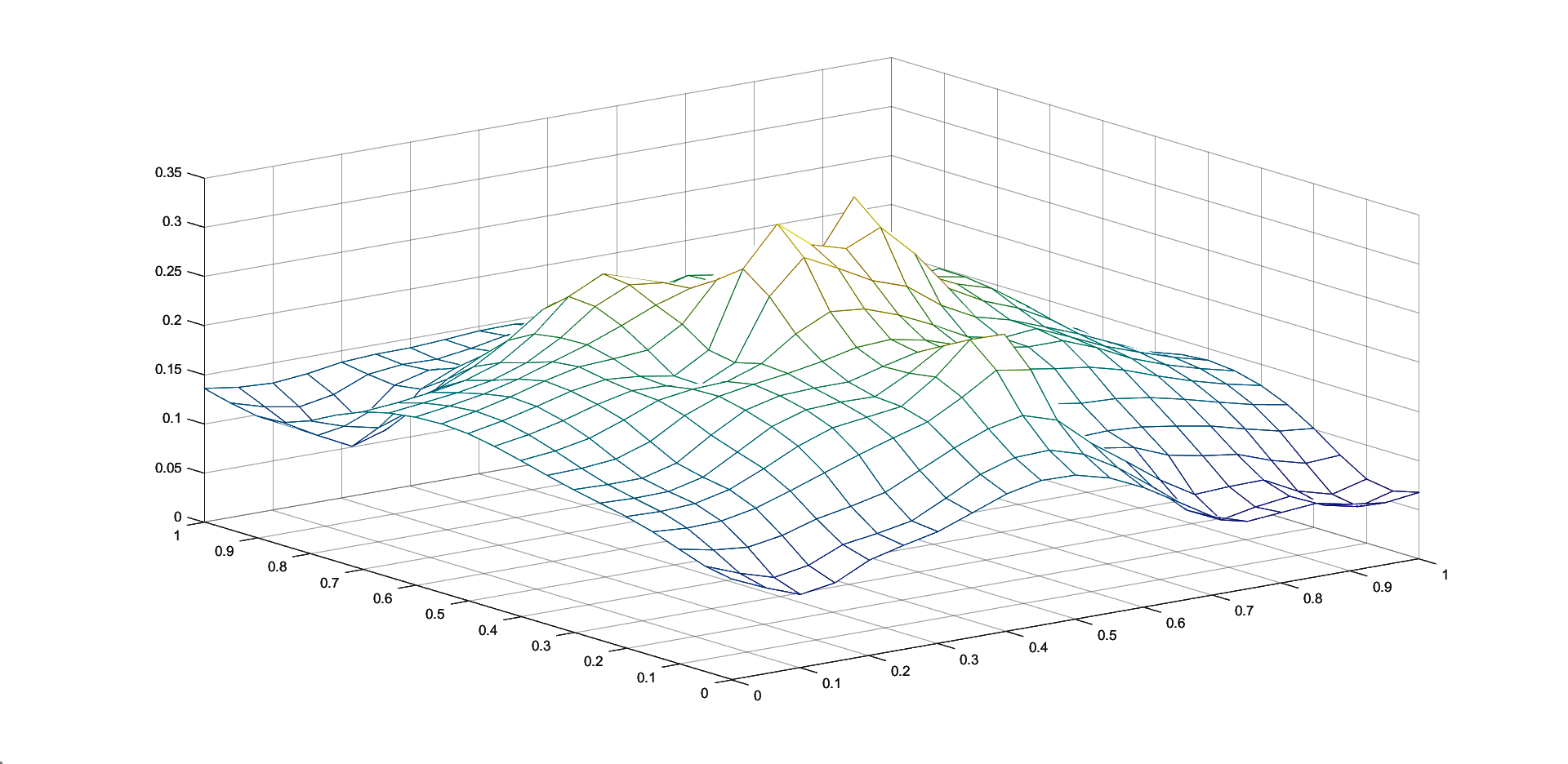
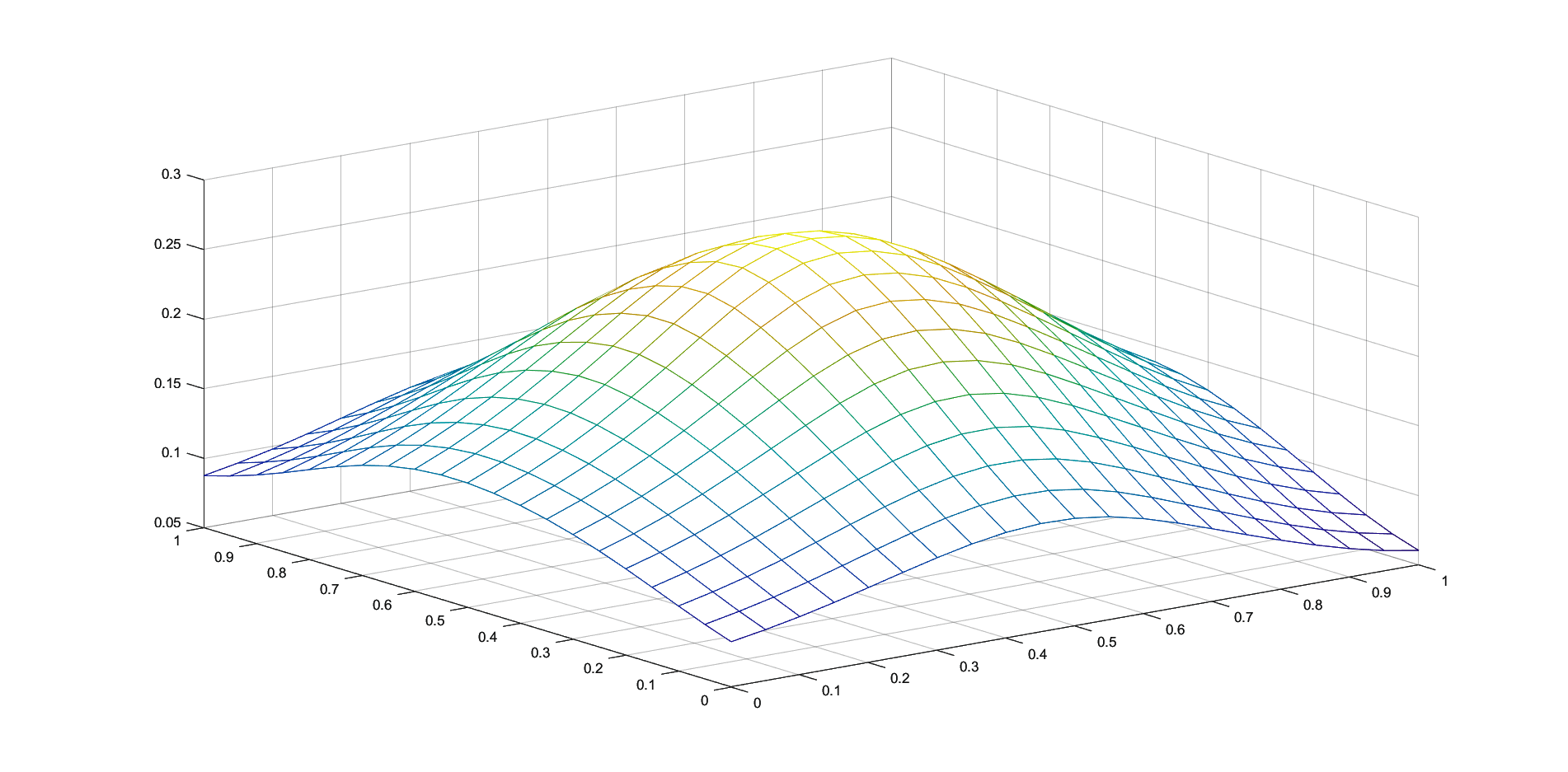
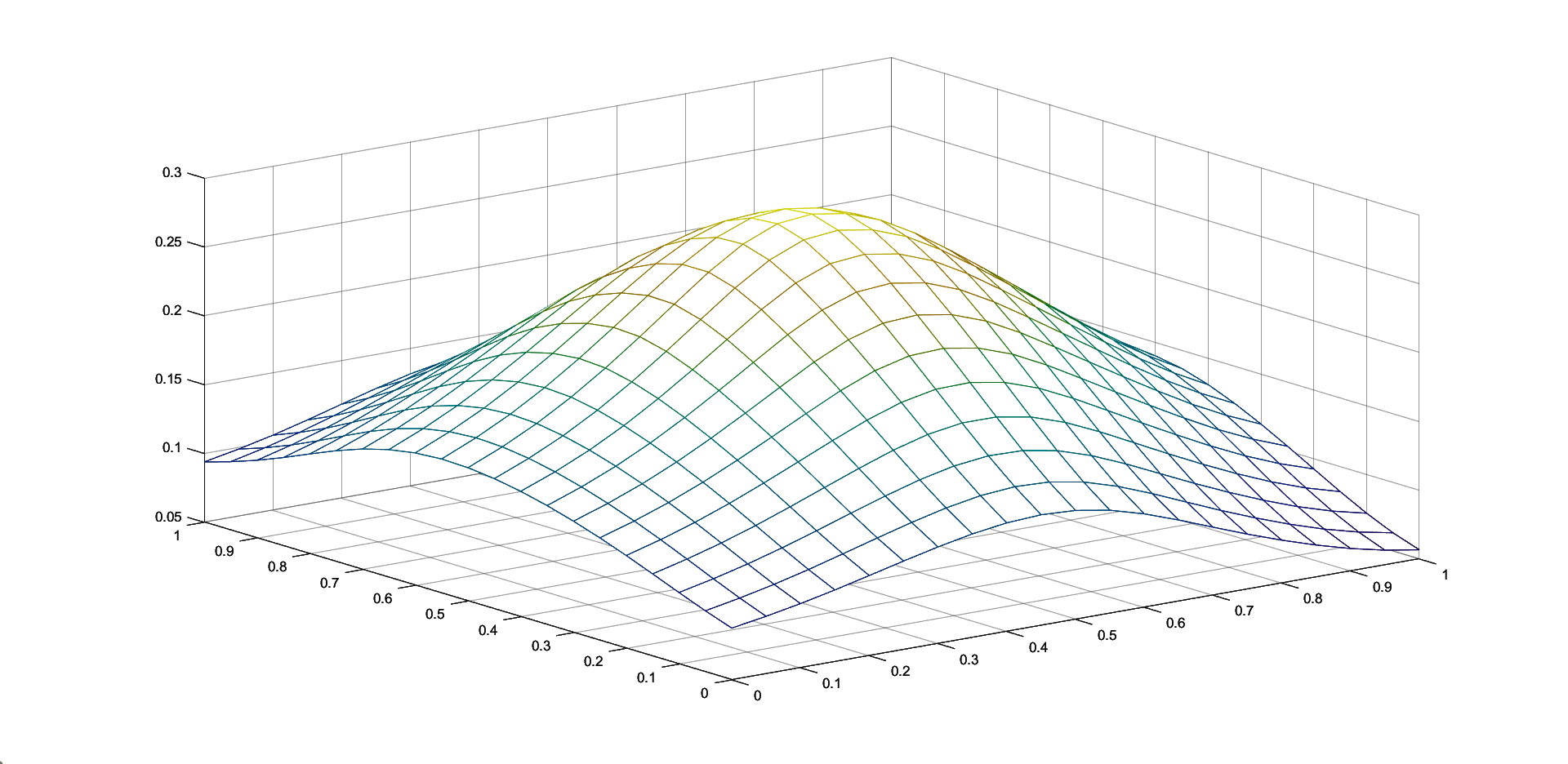
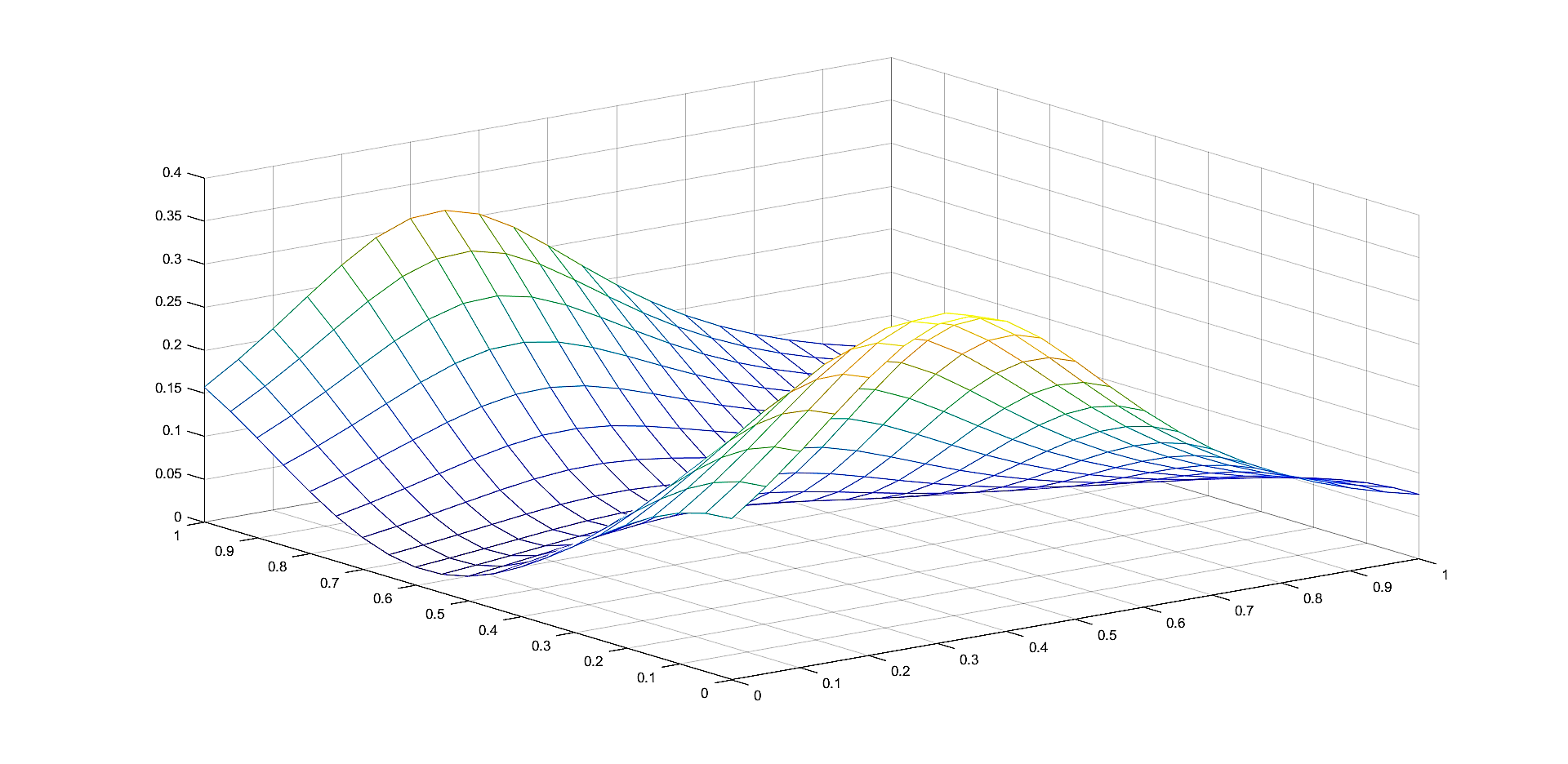
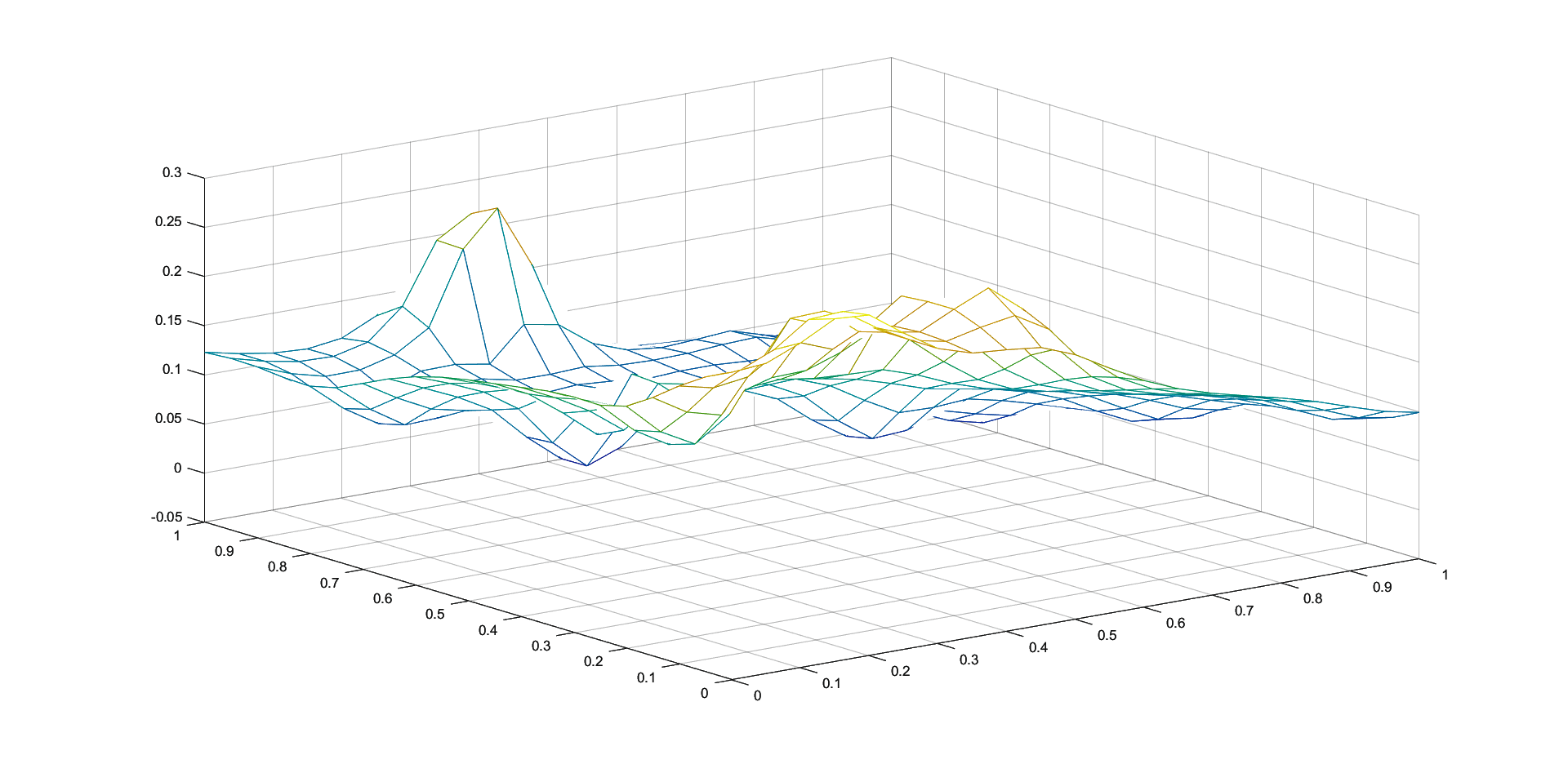
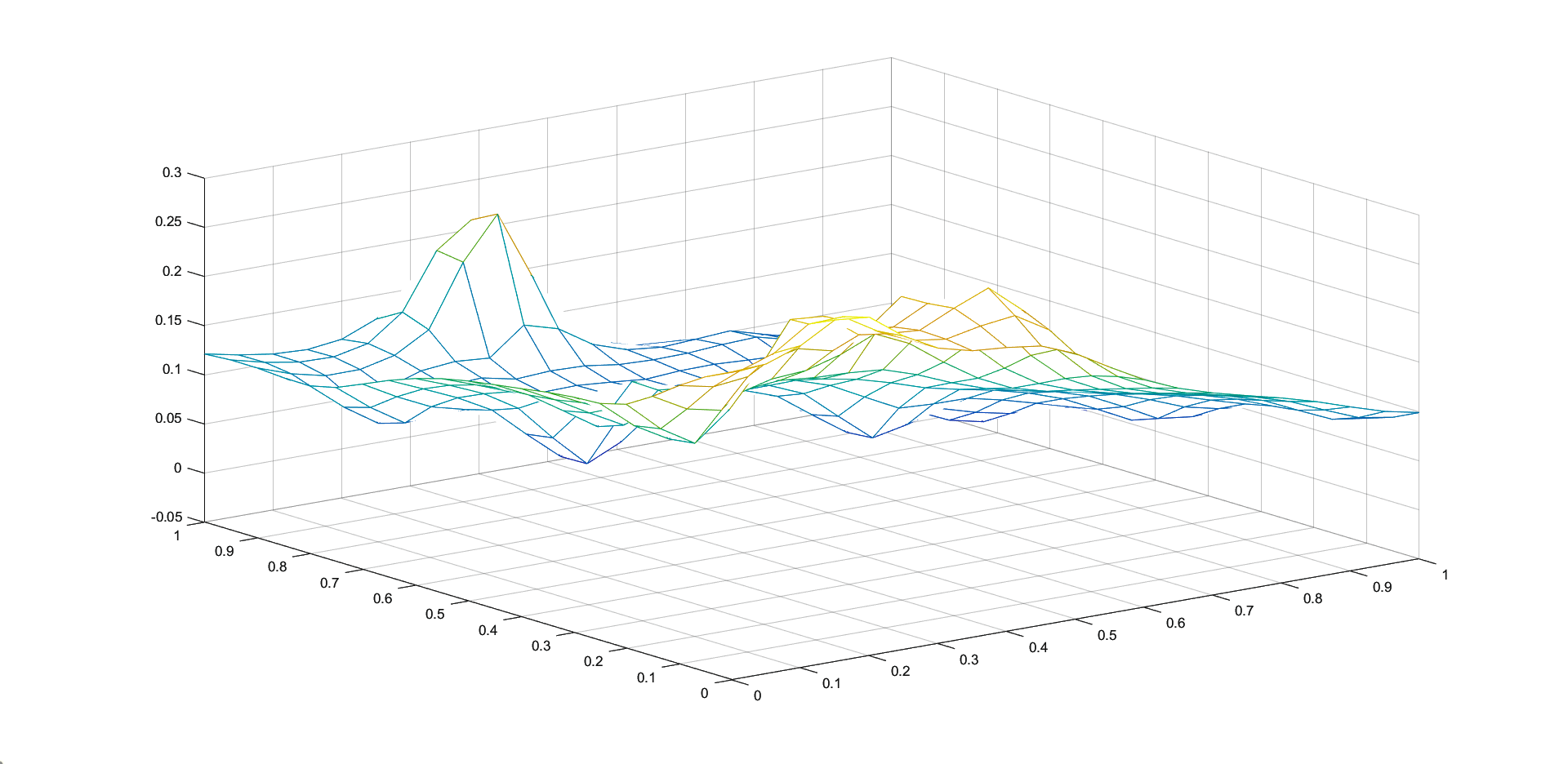
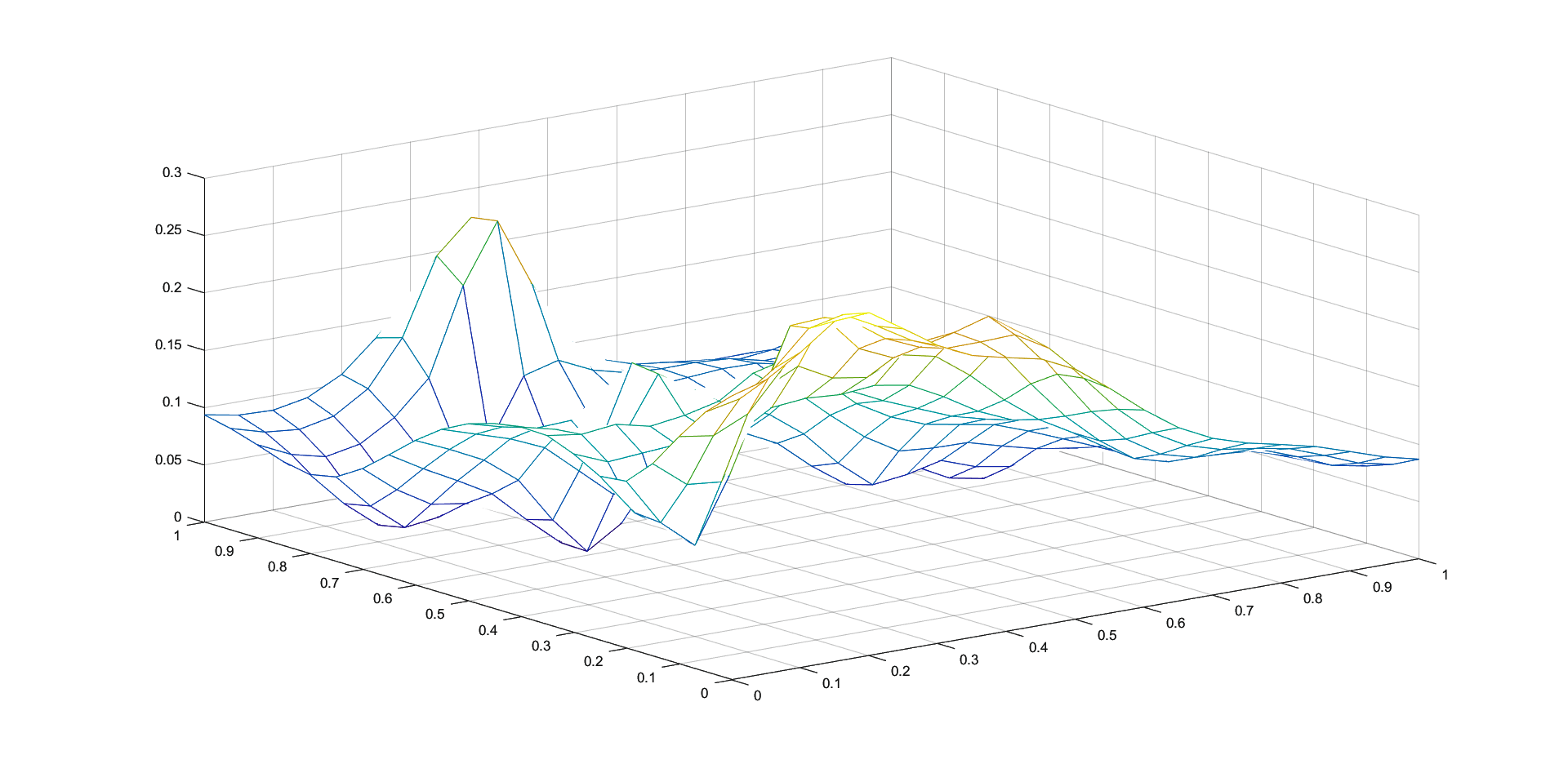
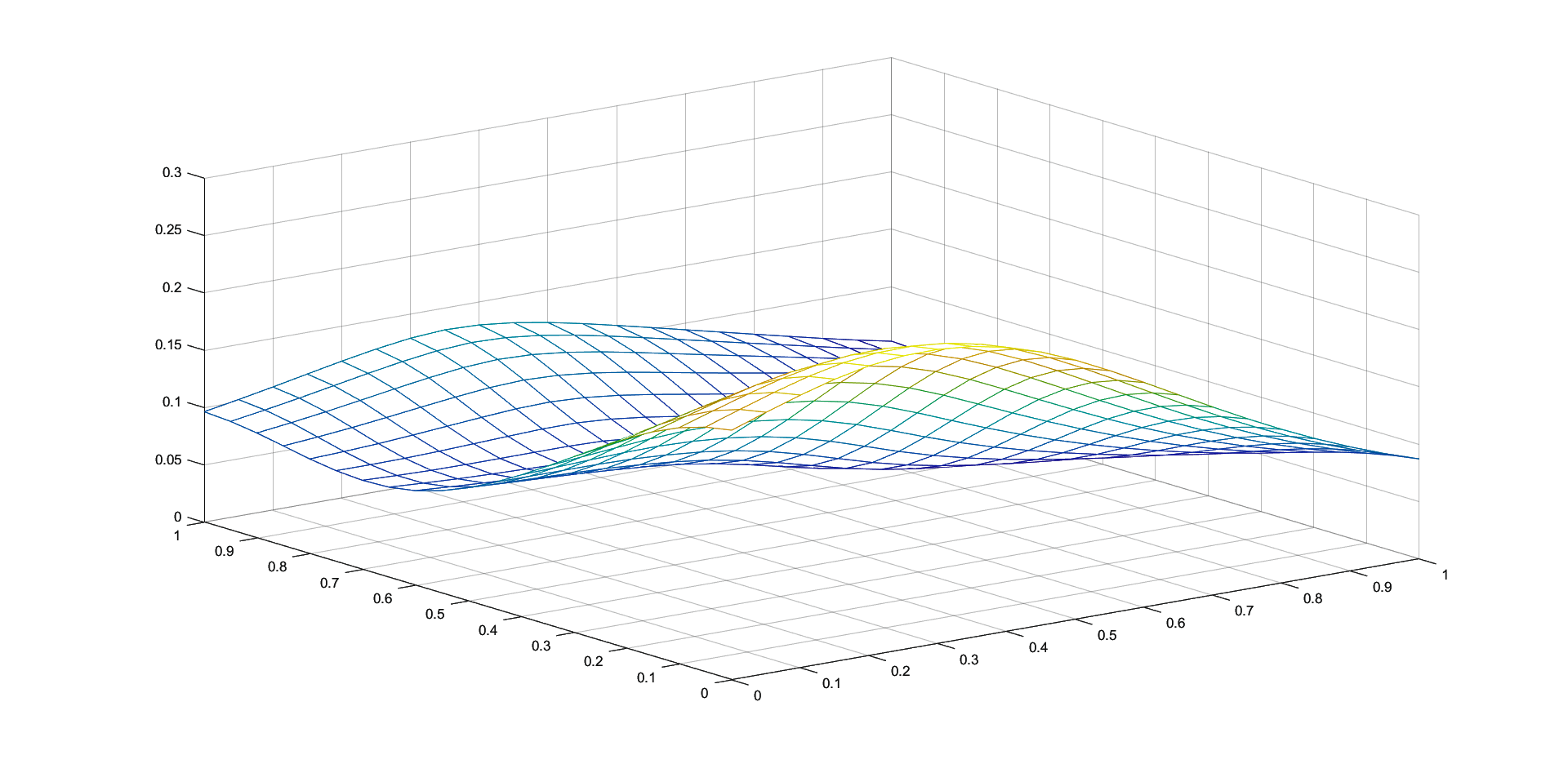
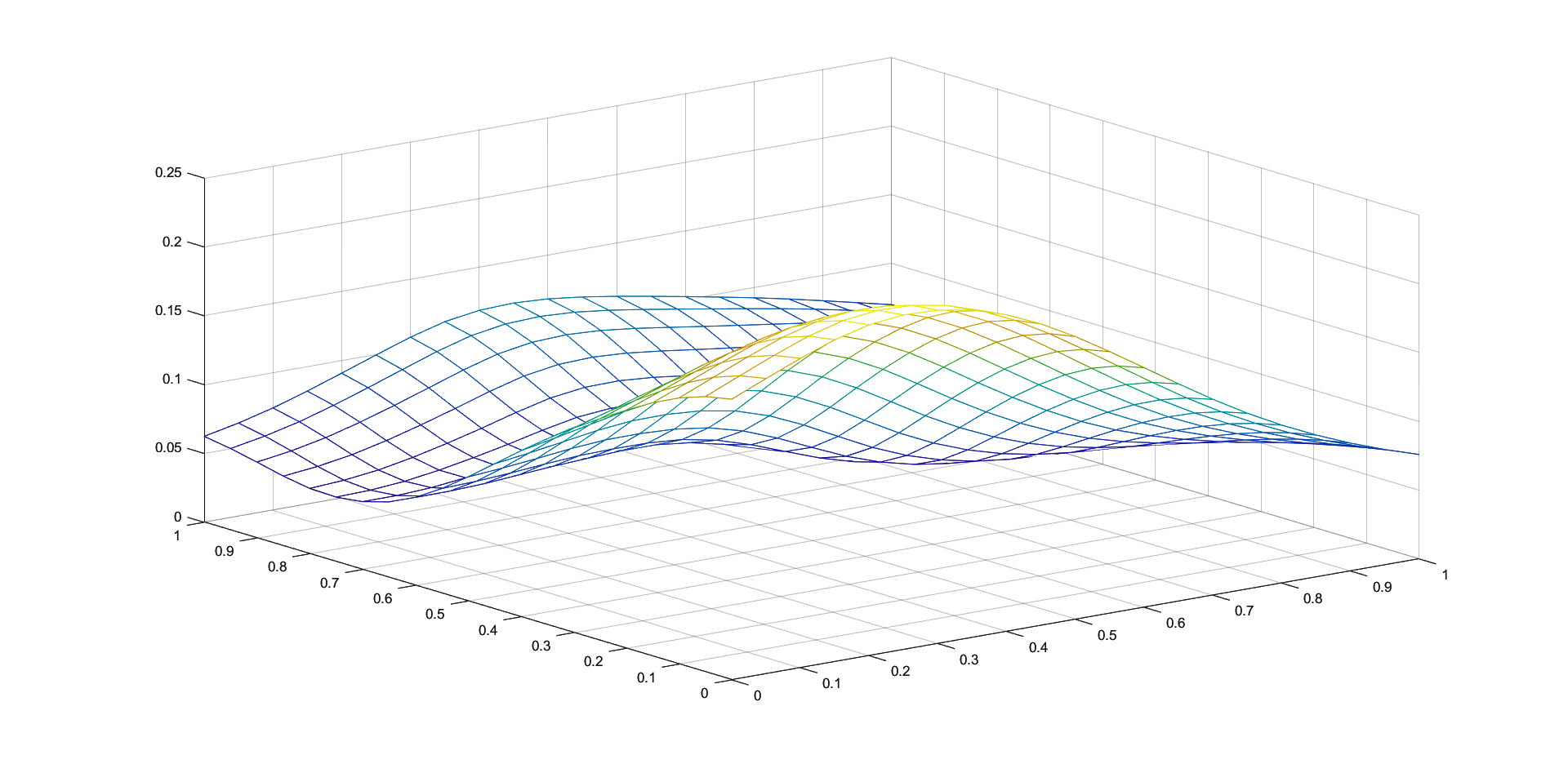
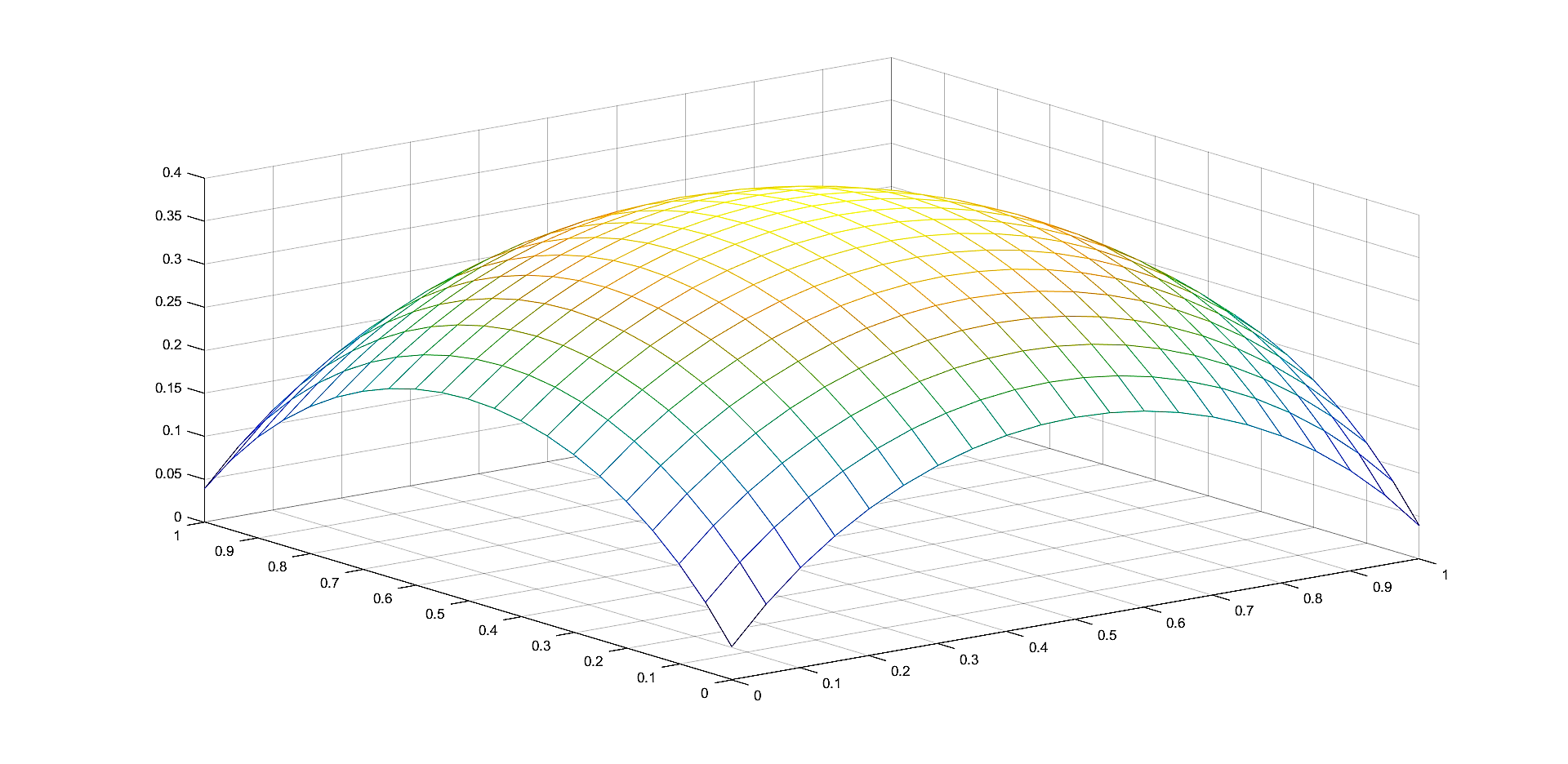
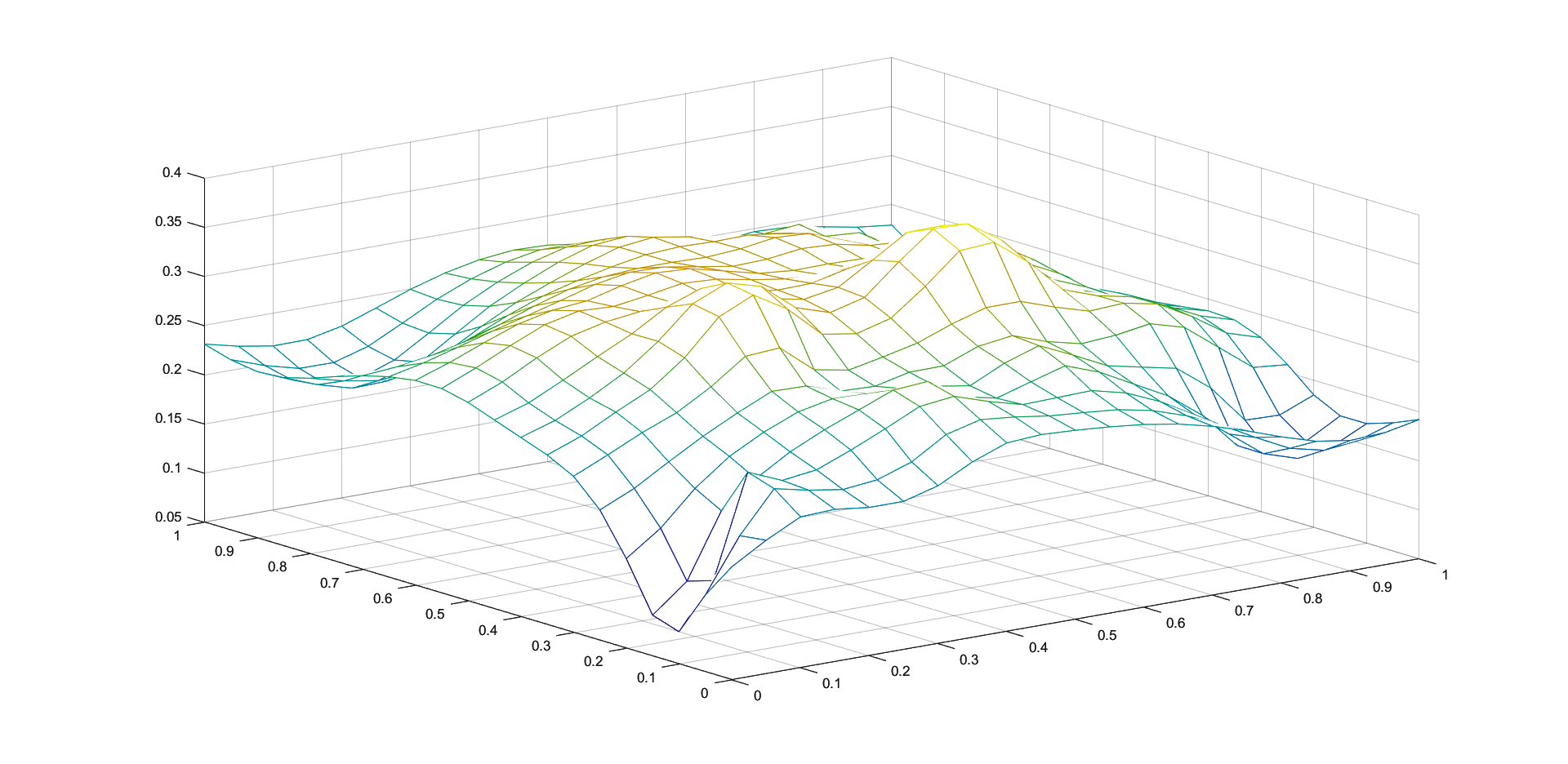
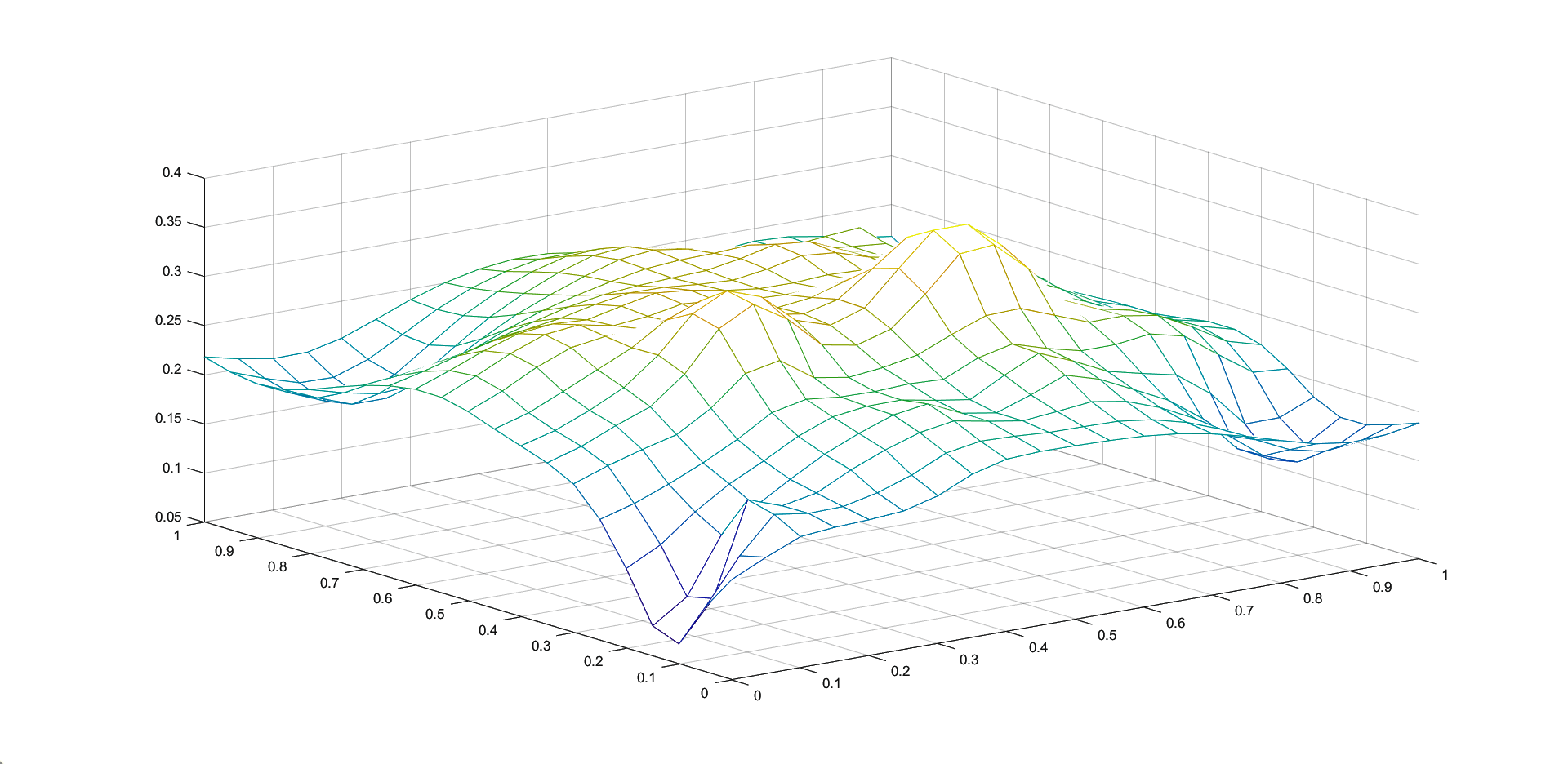
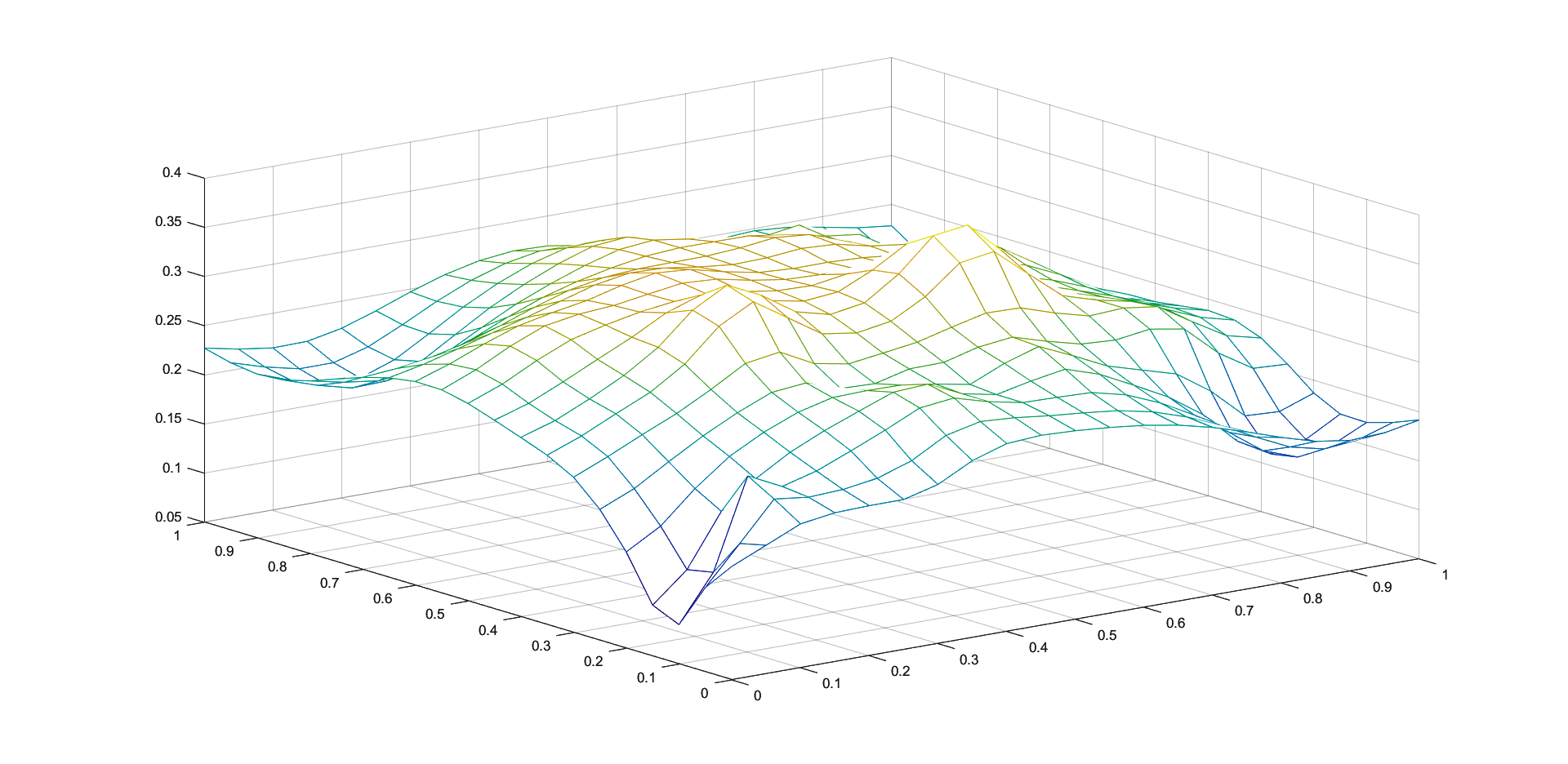
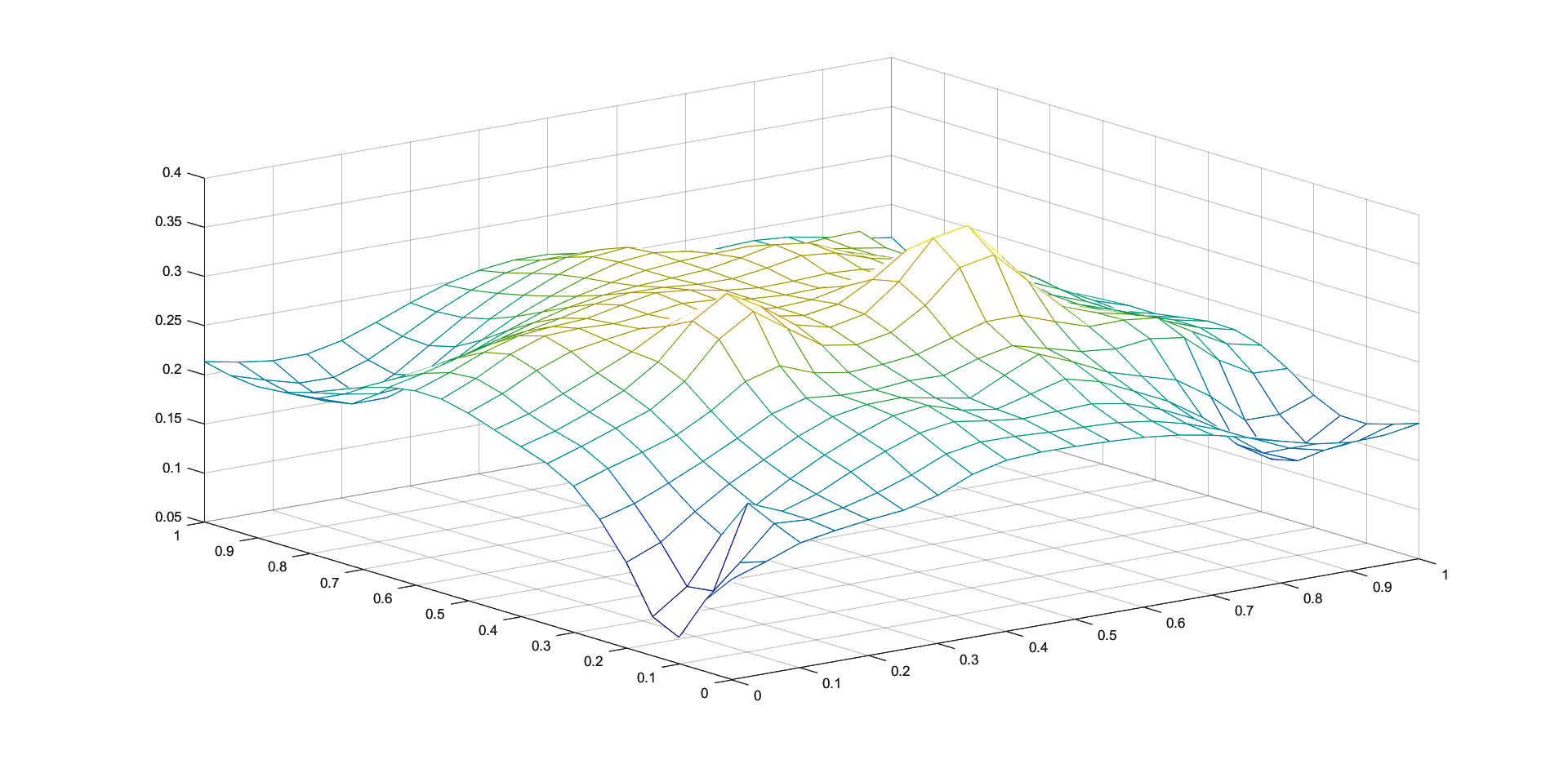
In Figures 9 - 27 we plot the graphs of \(f_1,\; f_2,\; f_3\) and of the corresponding Shepard operators \(S_{\mu }^{\beta }f\), \(S_{W}^{\beta }f\) and \(u_{\phi ^{\beta }}\), combined with the inverse quadratic (\(\beta = -1 \)) and the inverse multiquadric (\(\beta = -1/2 \)) radial basis functions. We consider the sets of the \(k=25\) representative knot points.

We remark that \(S_{W}^{\beta }f\) and \(u_{\phi ^{\beta }}\) have better approximation properties than the classical Shepard operator \(S_{\mu }^{\beta }f\), the results for \(u_{\phi ^{\beta }}\) depending on the values of \(\gamma \). Also, we notice better approximation errors for the lower number of knots obtained using the Algorithm 2.4.

\includegraphics[height=4in, width=5.0776in]{f1.png}
Figure 1 Function \(f_1\).

\includegraphics[height=4in, width=5.0776in]{clasic-f1-eps5-5-phi1.png}
Figure 2 \(S_{\mu }^{-1}f_1,\; \epsilon =5.5\).

\includegraphics[height=4in, width=5.0776in]{clasic-f1-eps10-phi2.png}
Figure 3 \(S_{\mu }^{-1/2}f_1,\; \epsilon =10\).

\includegraphics[height=4in, width=5.0776in]{modificat-f1-eps-5-5-phi1.png}
Figure 4 \(S_{W}^{-1}f_1,\; \epsilon =5.5\).

\includegraphics[height=4in, width=5.0776in]{modificat-f1-eps10-phi2.png}
Figure 5 \(S_{W}^{-1/2}f_1,\; \epsilon =10\).

\includegraphics[height=4in, width=5.0776in]{iterativ-f1-eps-5-5-phi1-gamma091.png}
Figure 6 \(u_{\phi ^{-1}},\; \epsilon =5.5,\; 0.91\).

\includegraphics[height=4in, width=5.0776in]{iterativ-f1-eps-10-phi2-gamma091.png}
Figure 7 \(u_{\phi ^{-1/2}},\; \epsilon =10,\; 0.91\).

Figure 8 Graphs for \(f_1\).


\includegraphics[height=4in, width=5.0776in]{f2.png}
Figure 9 Function \(f_2\).

\includegraphics[height=4in, width=5.0776in]{clasic-f2-eps10-phi1.png}
Figure 10 \(S_{\mu }^{-1}f_2,\; \epsilon =10\).

\includegraphics[height=4in, width=5.0776in]{clasic-f2-eps10-phi2.png}
Figure 11 \(S_{\mu }^{-1/2}f_2,\; \epsilon =10\).

\includegraphics[height=4in, width=5.0776in]{modificat-f2-eps-10-phi1.png}
Figure 12 \(S_{W}^{-1}f_2,\; \epsilon =10\).

\includegraphics[height=4in, width=5.0776in]{modificat-f2-eps-10-phi2.png}
Figure 13 \(S_{W}^{-1/2}f_2,\; \epsilon =10\).

\includegraphics[height=4in, width=5.0776in]{iterativ-f2-eps-10-phi1-gamma091.png}
Figure 14 \(u_{\phi ^{-1}},\; \epsilon =10,\; 0.91\).

\includegraphics[height=4in, width=5.0776in]{iterativ-f2-eps-10-phi2-gamma091.png}
Figure 15 \(u_{\phi ^{-1/2}},\; \epsilon =10,\; 0.91\).

Figure 16 Graphs for \(f_2\).


\includegraphics[height=4in, width=5.0776in]{f3.png}
Figure 17 Function \(f_3\).

\includegraphics[height=4in, width=5.0776in]{clasic-f3-eps5-5-phi1.png}
Figure 18 \(S_{\mu }^{-1}f_3,\; \epsilon =5.5\).

\includegraphics[height=4in, width=5.0776in]{clasic-f3-eps9-phi2.png}
Figure 19 \(S_{\mu }^{-1/2}f_3,\; \epsilon =9\).

\includegraphics[height=4in, width=5.0776in]{modificat-f3-eps-5-5-phi1.png}
Figure 20 \(S_{W}^{-1}f_3,\; \epsilon =5.5\).

\includegraphics[height=4in, width=5.0776in]{modificat-f3-eps-9-phi2.png}
Figure 21 \(S_{W}^{-1/2}f_3,\; \epsilon =9\).

\includegraphics[height=4in, width=5.0776in]{iterativ-f3-eps-5-5-phi1-gamma091.png}
Figure 22 \(u_{\phi ^{-1}},\; \epsilon =5.5,\; 0.91\).

\includegraphics[height=4in, width=5.0776in]{iterativ-f3-eps-9-phi2-gamma091.png}
Figure 23 \(u_{\phi ^{-1/2}},\; \epsilon =9,\; 0.91\).

Figure 24 Graphs for \(f_3\).


Table 1 Maximum approximation errors for the Gentle function.
 

\(\epsilon \)

Classical \(S_{\mu }\)

Modified \(S_{W}\)

Iterative \(u_{\phi }\)

   

k=25

N=100

k=25

N=100

\(\gamma \) (input)

k=25

N=100

\(f_1\)

–

0.0864

0.0855

0.0725

0.0644

\(0.66\)

0.0967

0.1158

           

\(0.84\)

0.0757

0.1159

           

\(0.91\)

0.0528

0.1105

\(\phi ^{-1}\)

5.5

0.1023

0.5564

0.0994

0.5543

\(0.66\)

0.1061

0.2866

           

\(0.84\)

0.0847

0.2644

           

\(0.91\)

0.0627

0.2396

 

10

0.1313

0.1876

0.1293

0.1681

\(0.66\)

0.1026

0.1488

           

\(0.84\)

0.0772

0.1251

           

\(0.91\)

0.0579

0.1123

\(\phi ^{-1/2}\)

9

0.1098

0.2402

0.1063

0.2219

\(0.66\)

0.1002

0.2155

           

\(0.84\)

0.0866

0.1985

           

\(0.91\)

0.0686

0.1887

 

10

0.1129

0.2292

0.1096

0.2094

\(0.66\)

0.0994

0.1936

           

\(0.84\)

0.0854

0.1750

           

\(0.91\)

0.0673

0.1653

Table 2 Maximum approximation errors for the Saddle function.
 

\(\epsilon \)

Classical \(S_{\mu }\)

Modified \(S_{W}\)

Iterative \(u_{\phi }\)

   

k=25

N=100

k=25

N=100

\(\gamma \) (input)

k=25

N=100

\(f_2\)

–

0.1096

0.1152

0.0970

0.1033

\(0.66\)

0.2083

0.2051

           

\(0.84\)

0.1902

0.1828

           

\(0.91\)

0.1633

0.1567

\(\phi ^{-1}\)

7

0.1669

0.9372

0.1575

0.8615

\(0.66\)

0.2198

0.3754

           

\(0.84\)

0.2103

0.4007

           

\(0.91\)

0.1938

0.4456

 

10

0.1813

0.1693

0.1828

0.1697

\(0.66\)

0.2175

0.1909

           

\(0.84\)

0.2045

0.1797

           

\(0.91\)

0.1825

0.1626

\(\phi ^{-1/2}\)

9

0.1677

0.5409

0.1639

0.4933

\(0.66\)

0.2301

0.3125

           

\(0.84\)

0.2222

0.3202

           

\(0.91\)

0.2077

0.3344

 

10

0.1582

0.2952

0.1630

0.2659

\(0.66\)

0.2292

0.2000
           

\(0.84\)

0.2195

0.2020

           

\(0.91\)

0.2029

0.2028

Table 3 Maximum approximation errors for the Sphere function.
 

\(\epsilon \)

Classical \(S_{\mu }\)

Modified \(S_{W}\)

Iterative \(u_{\phi }\)

   

k=25

N=100

k=25

N=100

\(\gamma \) (input)

k=25

N=100

\(f_3\)

–

0.2011

0.2156

0.1934

0.1744

\(0.66\)

0.1837

0.1850

           

\(0.84\)

0.1730

0.1743

           

\(0.91\)

0.1593

0.1645

\(\phi ^{-1}\)

5

0.1849

1.3107

0.1806

1.1997

\(0.66\)

0.1576

0.2703
           

\(0.84\)

0.1488

0.4361

           

\(0.91\)

0.1390

0.5255

 

5.5

0.1926

0.9074

0.1898

0.8297

\(0.66\)

0.1637

0.1925
           

\(0.84\)

0.1533

0.2901

           

\(0.91\)

0.1456

0.3494

\(\phi ^{-1/2}\)

7

0.1584

0.8948

0.1526

0.8150

\(0.66\)

0.1401

0.2258
           

\(0.84\)

0.1291

0.3072

           

\(0.91\)

0.1183

0.3464

 

9

0.1796

0.3682

0.1779

0.3341

\(0.66\)

0.1537

0.1772
           

\(0.84\)

0.1417

0.2091

           

\(0.91\)

0.1344

0.2216

1

Buhmann, M. D., Radial basis functions, Acta Numerica, 9(2000), pp. 1–38.

2

Cătinaş, T., The combined Shepard-Abel-Goncharov univariate operator, Rev. Anal. Numér. Théor. Approx., 32(2003), pp. 11–20.

3

Cătinaş, T., The combined Shepard-Lidstone bivariate operator, In: de Bruin, M.G. et al. (eds.): Trends and Applications in Constructive Approximation. International Series of Numerical Mathematics, Springer Group-Birkhäuser Verlag, 151(2005), pp. 77–89.

4

Cătinaş, T., The bivariate Shepard operator of Bernoulli type, Calcolo, 44 (2007), no. 4, pp. 189-202.

5

Cătinaş, T., Malina, A., Shepard operator of least squares thin-plate spline type, Stud. Univ. Babeş-Bolyai Math., 66(2021), no. 2, pp. 257-265.

6

Coman, Gh., The remainder of certain Shepard type interpolation formulas, Studia UBB Math, 32 (1987), no. 4, pp. 24-32.

7

Coman, Gh., Hermite-type Shepard operators, Rev. Anal. Numér. Théor. Approx., 26(1997), 33–38.

8

Coman, Gh., Shepard operators of Birkhoff type, Calcolo, 35(1998), pp. 197–203.

9

Farwig, R., Rate of convergence of Shepard’s global interpolation formula, Math. Comp., 46(1986), pp. 577–590.

10

Franke, R., Scattered data interpolation: tests of some methods, Math. Comp., 38(1982), pp. 181–200.

11

Franke, R., Nielson, G., Smooth interpolation of large sets of scattered data, Int. J. Numer. Meths. Engrg., 15(1980), pp. 1691–1704.

12

Hardy, R. L., Multiquadric equations of topography and other irregular surfaces, J. Geophys. Res., 76(1971), pp. 1905–1915.

13

Hardy, R. L., Theory and applications of the multiquadric–biharmonic method: 20 years of discovery 1968–1988, Comput. Math. Appl., 19(1990), pp. 163–-208.

14

Lazzaro, D., Montefusco, L.B., Radial basis functions for multivariate interpolation of large scattered data sets, J. Comput. Appl. Math., 140(2002), pp. 521–536.

15

Masjukov, A.V., Masjukov, V.V., Multiscale modification of Shepard’s method for interpolation of multivariate scattered data, Mathematical Modelling and Analysis, Proceeding of the 10th International Conference MMA2005 & CMAM2, 2005, pp. 467–472.

16

McMahon, J. R., Knot selection for least squares approximation using thin plate splines, M.S. Thesis, Naval Postgraduate School, 1986.

17

McMahon, J. R., Franke, R., Knot selection for least squares thin plate splines, Technical Report, Naval Postgraduate School, Monterey, 1987.

18

Micchelli, C. A., Interpolation of scattered data: distance matrices and conditionally positive definite functions, Constr. Approx., 2(1986), pp. 11–22.

19

Renka, R.J., Cline, A.K., A triangle-based \(C^{1}\) interpolation method. Rocky Mountain J. Math., 14(1984), pp. 223–237.

20

Renka, R.J., Multivariate interpolation of large sets of scattered data ACM Trans. Math. Software, 14(1988), pp. 139–148.

21

Shepard, D., A two dimensional interpolation function for irregularly spaced data, Proc. 23rd Nat. Conf. ACM, 1968, pp. 517–523.

22

Trımbiţaş, G., Combined Shepard-least squares operators - computing them using spatial data structures, Studia UBB Math, 47(2002), pp. 119–128.

23

Zuppa, C., Error estimates for moving least square approximations, Bull. Braz. Math. Soc., New Series 34(2), 2003, pp. 231-249.

[1] Buhmann, M.D., Radial basis functions, Acta Numerica, 9(2000), 1-38.
[2] Catinas, T., The combined Shepard-Abel-Goncharov univariate operator, Rev. Anal. Numer. Theor. Approx., 32(2003), 11-20.
[3] Catinas, T., The combined Shepard-Lidstone bivariate operator, In: de Bruin, M.G. et al. (eds.): Trends and Applications in Constructive Approximation. International Series of Numerical Mathematics, Springer Group-Birkhauser Verlag, 151(2005), 77-89.
[4] Catinas, T., The bivariate Shepard operator of Bernoulli type, Calcolo, 44(2007), no. 4, 189-202.
[5] Catinas, T., Malina, A., Shepard operator of least squares thin-plate spline type, Stud. Univ. Babes-Bolyai Math., 66(2021), no. 2, 257-265.
[6] Coman, Gh., The remainder of certain Shepard type interpolation formulas, Stud. Univ. Babes-Bolyai Math., 32(1987), no. 4, 24-32.
[7] Coman, Gh., Hermite-type Shepard operators, Rev. Anal. Numer. Theor. Approx., 26(1997), 33-38.
[8] Coman, Gh., Shepard operators of Birkhoff type, Calcolo, 35(1998), 197-203.
[9] Farwig, R., Rate of convergence of Shepard’s global interpolation formula, Math. Comp., 46(1986), 577-590.
[10] Franke, R., Scattered data interpolation: tests of some methods, Math. Comp., 38(1982), 181-200.
[11] Franke, R., Nielson, G., Smooth interpolation of large sets of scattered data, Int. J. Numer. Meths. Engrg., 15(1980), 1691-1704.
[12] Hardy, R.L., Multiquadric equations of topography and other irregular surfaces, J. Geophys. Res., 76(1971), 1905-1915.
[13] Hardy, R.L., Theory and applications of the multiquadric biharmonic method: 20 years of discovery 1968-1988, Comput. Math. Appl., 19(1990), 163-208.
[14] Lazzaro, D., Montefusco, L.B., Radial basis functions for multivariate interpolation of large scattered data sets, J. Comput. Appl. Math., 140(2002), 521-536.
[15] Masjukov, A.V., Masjukov, V.V., Multiscale modification of Shepard’s method for interpolation of multivariate scattered data, Mathematical Modelling and Analysis, Proceeding of the 10th International Conference MMA2005 & CMAM2, 2005, 467-472.
[16] McMahon, J.R., Knot selection for least squares approximation using thin plate splines, M.S. Thesis, Naval Postgraduate School, 1986.
[17] McMahon, J.R., Franke, R., Knot selection for least squares thin plate splines, Technical Report, Naval Postgraduate School, Monterey, 1987.
[18] Micchelli, C.A., Interpolation of scattered data: distance matrices and conditionally positive definite functions, Constr. Approx., 2(1986), 11-22.
[19] Renka, R.J., Multivariate interpolation of large sets of scattered data, ACM Trans. Math. Software, 14(1988), 139-148.
[20] Renka, R.J., Cline, A.K., A triangle-based C1 interpolation method, Rocky Mountain J. Math., 14(1984), 223-237.
[21] Shepard, D., A two dimensional interpolation function for irregularly spaced data, Proc. 23rd Nat. Conf. ACM, 1968, 517-523.
[22] Trimbitas, G., Combined Shepard-least squares operators – computing them using spatial data structures, Stud. Univ. Babes-Bolyai Math., 47(2002), 119-128.
[23] Zuppa, C., Error estimates for moving least square approximations, Bull. Braz. Math. Soc., New Series, 34(2003), no. 2, 231-249.

Related Posts

No results found.