Abstract
We solve numerically the nonlinear and double singular boundary value problem formed by the well known Emden-Fowler equation \(u^{\prime\prime}=u^{s}x^{-1/2},s>1\) along with the boundary conditions \(u(0)=1\) and \(u(\infty)=0\). In order to capture the exponential decrease of its solution we use the Laguerre-Gauss-Radau collocation method and infer its convergence. We show that the value of \(u^{\prime}\) at origin, which plays a fundamental role in these problems, definitely satisfies some rigorous accepted bounds. A particular attention is paid to the Thomas-Fermi case, i.e. \(s:=3/2\). We treat the problems as boundary values ones without any involvement of ones with initial values. The method is robust with respect to scaling and order of approximation.
Authors
C.I. Gheorghiu
“Tiberiu Popoviciu” Institute of Numerical Analysis, Romanian Acdemy
Keywords
Emden-Fowler problem; Laguerre collocation; slope in origin; bounds
Paper coordinates
C.I. Gheorghiu, Accurate Laguerre collocation solutions to a class of Emden–Fowler type BVP, ,
About this paper
Journal
Journal of Physics A: Mathematical and Theoretical
Publisher Name
IOP Publishing Ltd.
Print ISSN
17518113
Online ISSN
17518121
google scholar link
Paper (preprint) in HTML form
Accurate Laguerre Collocation Solutions to a Class of Emden-Fowler Type BVP
Abstract
We solve numerically the nonlinear and double singular boundary value problem (BVP) formed by the well known Emden-Fowler (EF) equation , along with the boundary conditions and In order to capture the exponential decrease of its solution we use the Laguerre-Gauss-Radau collocation (LGRC) method and infer its convergence. We show that the value of at origin, which plays a fundamental role in these problems, definitely satisfies some rigorous accepted bounds. A particular attention is paid to the Thomas-Fermi (TF) case, i.e., We treat the problems as boundary values ones without any involvement of ones with initial values. The method is robust with respect to scaling and order of approximation.
Keywords: Emden-Fowler problem, Laguerre collocation, slope in origin, bounds.
1 Introduction
Various boundary value problems associated to EF equation have been treated along time by transforming them into initial value problems. Furthermore, they have been solved with different classical numerical methods of various accuracy.
The IVP in physics as well as in other branches of science, have been solved by various shooting methods. These methods have become obsolete over time for many reasons.
We appreciate that solving boundary problems with (their) specific numerical methods is important in order to obtain better outgoings.
Consider the Emden-Fowler equation
| (1) |
supplied with the same boundary condition as above, i.e.,
| (2) |
When the solution of this equation decays as , , as approaches (see [4] and the papers quoted there).
The existence of the solution to such a problem is substantiated in the paper [1]. In [4] the author finds very accurate a priori bounds for the slope He exploits the integral properties of EF equation and produces the double inequality
| (3) |
Thus, the collocation spectral methods, in conventional form or more recent Chebfun form, more elegant, easier to implement and more accurate are well suited for solving the problems at hand.
In the case of the problems examined in this article, the Laguerre polynomials, multiplied by the weight function correctly represent the continuous functions on the real semi-axis and satisfy the boundary condition at infinity (the second condition in (2)).
Conventional spectral methods have been exploited almost to exhaustion solving physics problems by J P Boyd [6].
The main aim of this study is to show that the LGRC method solves problems of type (1)–(2) fairly accurate such that the slope in origin satisfies bounds like (3). Moreover we infer on the convergence of this algorithm.
Delkhosh and Parand have recently published several papers on the Emden-Fowler problem from which we only quote [9]. They confirm the efficiency and accuracy of the spectral methods using the generalized fractional order of the Chebyshev orthogonal functions. The purpose of our work is only to eliminate the numerical noise from the value of the derivative of solution in origin. The extension of our study to non-integer values of is in progress.
For the particular case in [4] the author deduces the following important and useful integral identity
| (4) |
for any natural
Some clarifications are necessary for the convergence of the improper integral [5].
The solutions of problems (1)–(2) are continuous indefinitely differentiable functions with compact support on the real semi-axis, the integrand of integral I has the same property.
Under these conditions, the general theory of improper integrals ensures convergence.
For and we will show that the solutions obtained by LGRC satisfy the above integral identities with a quite good approximation. The final bounds for are in this case
| (5) |
In the paper [6] the author gives very interesting historical aspects related to the numerical solution of the TF problem, mentioning several Nobel Prize laureates who considered it. He lists a set of values for , not all of which belong to the range (3). Its solution is based on rational Chebyshev series.
2 LGRC in solving Thomas-Fermi b.v.p.
With respect to the LGRC method we refer to the monograph [5] which offers all the ingredients to implement the method.
Actually we are looking for a solution of the form
| (6) |
where
and and are the roots of , the Laguerre polynomial of degree indexed in increasing order of magnitude. The interval can be mapped to itself by the change of variables where is a positive real number called scaling factor. Thus LGRC method contains a free parameter which can be exploited to optimize the accuracy of differencing process and to tune the numerical outcomes.
In order to introduce the boundary conditions (2) we operate the change of variables
If we denote by the second order Laguerre differentiation matrix in physical space, LGRC cast the problem (1)–(2) with into the nonlinear algebraic system
| (7) |
where the vector contains the Gauss-Radau nodes and the vector the corresponding unknowns (see Weidemann and Reddy [3]). We have to observe that in formulating the system (7) we use the MATLAB notations (the under-dot in (7) signifies the pointwise product of the two areas in MATLAB).
We have solved the system (7) by MATLAB routine fsolve and have found the following value
which strictly belong to the interval (5). In order to find the slope at origin we simply multiply the vector solution with the first order derivative matrix.
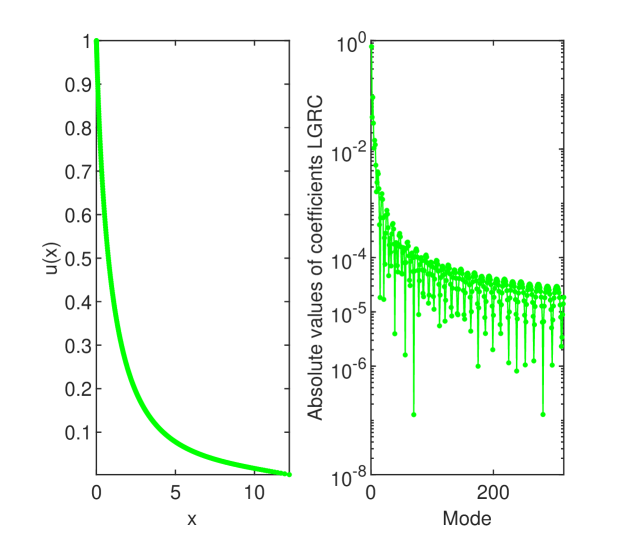
In the left panel of Figure 1 we display the solution to our problem and in the right panel we show how the coefficients of LGRC solution decrease. Roughly speaking we cannot hope to an accuracy much better than (see Boyd [2], Convergence of Spectral Methods). Actually, the way in which the coefficients decrease is a correct indication of convergence of solution.
We have to mention at this point that in order to get the coefficients of solution we have relied on the Laguerre polynomial transform between physical and coefficient spaces from [5].
With respect to the right panel in Figure 1, we have to observe that this technique was introduced by Boyd in his huge monograph [2]. It is not a precise proof but a very valuable trick. We have successfully and frequently used this argument.

With the value of displayed above we have validated numerically the integral relations (4). Thus, for the integral equality is correct to order and when the accuracy decreases to order
3 LGRC in solving Emden-Fowler BVP
We now consider the EF problem with in the equation (1) and a perfect similar treatment as above has been applied. For this value of exponent the bounds in (3) are the following
| (8) |
Our numerical experiments with scaling factor in interval and resolution around provided numerical values of the derivative in origin strictly in the interval (8).
The only cons of the method is the arbitrary choosing of the resolution .
4 Concluding remarks
In order to solve nonlinear BVP we can choose between Chebyshev or Fourier collocation methods, when the domain is finite, or Laguerre, sinc or Hermite polinomials based collocation, whenever the domain is unbounded. The choosing depends also on the shape of nonliniarity as well as on the packages of implementation at hand. We mention that the literature about these methods is now well established so we consider that more details are not necessary.
In order to validate problems (1)–(2) we have alternatively tried to use Chebyshev collocation in its conventional form (see [7]) or in form of Chebfun (see [8]) with two ingredients, namely domain truncation or the mapping of half line into the canonical interval None of these methods gave acceptable results.
It is clear that the success of the used LGRC method is due to the existence of the weighting factor in the definition of the LGR interpolant (6). The method handles correctly both singularities, at origin and at infinity, is robust with respect to the resolution and scaling, and is easy implementable. Up to our knowledge we consider that this method is, so far, the most accurate in solving such nonlinear and double singular problems as boundary value ones.
The author is indebted to both referees for opportune observations that led to the improvement of the work.
References
- [1] O’Regan D 1996 Can. J. Math. 48 143
- [2] Boyd J P 2000 Chebyshev and Fourier Spectral Methods, Dover Publications, Inc. 31 East 2nd Street, Mineola, New York 11501
- [3] Weidemann J A C and Reddy S C 2000 ACM Trans. Math. Softw. 26 465
- [4] Iacono R 2008 J. Phys. A: Math. Theor. 41 455204
- [5] Shen J, Tang T and Wang L - L 2011 Spectral Methods. Algorithms, Analysis and Applications (Springer-Verlag Berlin) Chapter 7
- [6] Boyd J P 2013 J. Comput. Appl. Math. 244 90
- [7] Gheorghiu C I 2014 Spectral Methods for Non-Standard Eigenvalue Problems. Fluid and Structural Mechanics and Beyoud, Springer Chapters 3 and 4
- [8] Tretehten L N, Birkisson A and Driscoll T A 2018 Exploring ODEs, SIAM Philadelphia, Appendix A
- [9] Delkhosh M and Parand K 2019 Hacet. J. Math. Stat. 48 1601
[1] Iacono R 2008 J. Phys. A: Math. Theor. 41 455204
[2] O’Regan D 1996 Can. J. Math. 48 143
[3] Boyd J P 2013 J. Comput. Appl. Math. 244 90
[4] Delkhosh M and Parand K 2019 Hacettepe J. Math. Stat. 48 1601
[5] Shen J, Tang T and Wang L – L 2011 Spectral Methods. Algorithms, Analysis and Applications (Berlin: Springer) ch 7
[6] Weidemann J A C and Reddy S C 2000 ACM Trans. Math. Softw. 26 465
[7] Boyd J P 2000 Chebyshev and Fourier Spectral Methods (New York: Dover) p 11501
[8] Gheorghiu C I 2014 Spectral Methods for Non-Standard Eigenvalue Problems. Fluid and Structural Mechanics and Beyoud (Berlin: Springer) ch 3 and 4
[9] Tretehten L N, Birkisson A and Driscoll T A 2018 Exploring ODEs (Philadelphia, PA:SIAM)
