Abstract
We present a new type of optimization algorithms, adapted for neural network training. These algorithms are based upon sequential operator splitting technique for some associated dynamical systems.
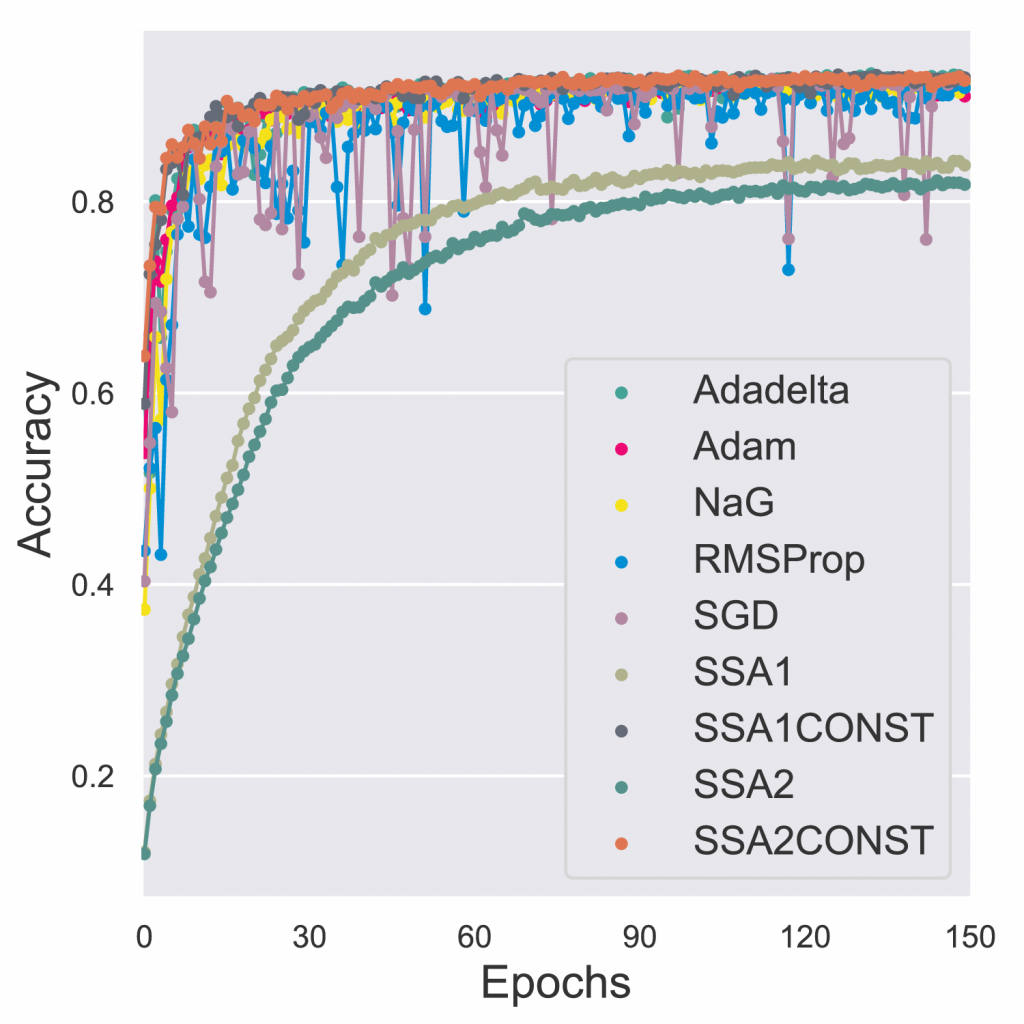
Furthermore, we investigate through numerical simulations the empirical rate of convergence of these iterative schemes toward a local minimum of the loss function, with some suitable choices of the underlying hyper parameters.
We validate the convergence of these optimizers using the results of the accuracy and of the loss function on the MNIST, MNIST-Fashion and CIFAR 10 classification datasets.
Authors
C.D. Alecsa
Faculty of Mathematics and Computer Science, Babes-Bolyai University, Cluj-Napoca, Romania
Tiberiu Popoviciu Institute of Numerical Analysis (Romanian Academy), Cluj-Napoca, Romania
T. Pinta
Mathematical Institute University of Oxford, Oxford, England
I. Boros
Faculty of Mathematics and Computer Science, Babes-Bolyai University, Cluj-Napoca, Romania
Tiberiu Popoviciu Institute of Numerical Analysis (Romanian Academy), Cluj-Napoca, Romania
Keywords
unconstrained optimization problems; splitting; neural network training;
Paper coordinates
C.-D. Alecsa, T. Pinta, I. Boros, New optimization algorithms for neural network training using operator splitting techniques, 126 (2020), pp. 178-190, doi: 10.1016/j.neunet.2020.03.018
About this paper
Print ISSN
0893-6080
Online ISSN
google scholar link
[1] Y. Bengio, Practical recommendations for gradient-based training of deep architectures, 2012,arXiv:1206.5533.
[2] C. Bishop, Training with noise is equivalent to Tikhonov regularization, Neural computation 7 (1),1995, 108– 116.
[3] L. Bottou, Stochastic gradient descent tricks, Neural networks: Tricks of the trade, Springer, 2012,421– 436.
[4] L. Bottou, F.E. Curtis, J. Nocedal, Optimization Methods for Large-Scale Machine Learning, SIAM Review, vol. 60, no. 2, 2018, 223-311
[5] R.I. Bot, E.R. Csetnek, S.C. László, An inertial forward-backward algorithm for minimizing the sum oftwo non-convex functions, Euro Journal on Computational Optimization 4(1), 2016, 3-25.
[6] A.B. Da Silva, M. Gazeau, A general system of differential equations to model first order adaptive algorithms, 2018, arXiv:1810.13108.
[7] T. Dozat, Incorporating Nesterov momentum into Adam, ICLR Workshop, 2016, 1-4.
[8] J. Duchi, E. Hazan, Y. Singer, Adaptive Subgradient Methods for Online Learning and Stochastic Optimization, Journal of Machine Learning Research, 2011, 2121–2159.
[9] I. Faragó, New operator splitting methods and their applications, Boyanov et al. (Eds.) NumericalMethods and Applications, Lecture Notes in Computational Sciences 4310, Springer Verlag, Berlin, 2007, 443-450.
[10] I. Goodfellow, Y. Bengio, A. Courville, Deep Learning, MIT Press, 2016,http://www.deeplearningbook.org.
[11] E. Hansen, A. Ostermann, Exponential splitting for unbounded operators, Mathematics ofcomputation, vol. 78, no. 267, 2009, 1485-1496.
[12] E. Hansen, F. Kramer, A. Ostermann, A second-order positivity preserving scheme for semilin-ear parabolic problems, Applied Numerical Mathematics, vol. 62, issue 10, 2012, 1428-1435.
[13] C.F. Higham, D.J. Higham, Deep learning : An introduction for applied mathematicians, 2018, arXiv:1801.05894.
[14] H. Holden, K.H. Karlsen, K-A. Lie, Splitting methods for Partial Differential Equations with Rough Solutions : Analysis and MATLAB Programs, European Mathematical Society Publishing House, 2010,DOI:10.4171/078.16
APREPRINT – JUNE 18, 2019
[15] D.P. Kingma, J.L. Ba, Adam : A method for stochastic optimization, 2014,arXiv:1412.6980.
[16] Y. LeCun, L. Bottou, G.B. Orr, K.R. Müller, Efficient backprop, Neural networks: Tricks of thetrade, Springer, 1998, 9–50.
[17] G.I. Marchuk, Some application of splitting-up methods to the solution of mathematical physics problems, Aplikace matematiky, 1968, 103–132.
[18] P. Mehta, M. Bukov, C.H. Wang, A.G.R. Day, C. Richardson, C.K. Fisher, and D.J. Schwab, AHigh-Bias, Low-Variance Introduction to Machine Learning for Physicists, 2018, arXiv:1803.08823.
[19] Y. Nesterov, A method of solving a convex programming problem with convergence rate o(1/k2), Soviet Mathematics Doklady, vol. 27, 1983, 372–376.
[20] M. Nielsen, Neural Networks and Deep Learning, Determination Press, 2015.
[21] J. Nocedal, S. Wright, Numerical Optimization, Springer-Verlag, New York, 2006,10.1007/978-0-387-40065-5.
[22] B. Polyak, Some methods of speeding up the convergence of iteration methods, USSR ComputationalMathematics and Mathematical Physics, 4 (5), 1964, 1–17.
[23] S. Ruder, An overview of gradient descent optimization algorithms, 2016, arXiv:1609.04747.
[24] L. Smith, Cyclical learning rates for training neural networks, 2015, arXiv:1506.01186.
[25] G. Strang, On the construction and comparison of difference schemes, SIAM J. Numerical Anaysis,vol. 5, no. 3, 1968, 506-517.
[26] W. Su, S. Boyd, E.J. Candes, A differential equation for modeling Nesterov’s accelerated gradientmethod: theory and insights, Journal of Machine Learning Research, (17), 2016, 1-43.
[27] T. Sun, P. Yin, D. Li, C. Huang, L. Guan, H. Jiang, Non-ergodic Convergence Analysis of Heavy-Ball Algorithms, 2018, https://arxiv.org/abs/1811.01777.
[28] I. Sutskever, J. Martens, G. Dahl, G. Hinton , On the importance of initialization and mo-mentum in deep learning, International conference on machine learning, 2013, 1139–1147.
[29] C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, A.Rabinovich, Going deeper with convolutions, CVPR, 2015, arxiv.org/pdf/1409.4842.pdf.
[30] T. Tieleman, G. Hinton, Lecture 6.5 – rmsprop. Divide the gradient by a running average ofits recent magnitude, Coursera : Neural Networks for Machine Learning, 4, 2012.
[31] A.C. Wilson, R. Roelofs, M. Stern, N. Srebro, and B. Recht, The marginal value of adaptive gradient methods in machine learning, 2017, arXiv:1705.08292.
[32] M.D. Zeiler, ADADELTA : An adaptive learning rate method, 2012,http://arxiv.org/abs/1212.5701.
[33] C. Zhang, S. Bengio, M. Hardt, B. Recht, O. Vinyals, Understanding deep learning requires rethinking generalization, 2016, arXiv:1611.03530.17