The strict superlinear order can be faster than the infinite order

1 year ago

(original), Convergence order, ISI/JCR, Numerical Analysis, paper

Abstract

The strict superlinear order (superlinear convergence) was usually regarded as having an intermediate speed between between linear and with order $p>1$.

In this paper we analyze the superlinear convergence (superlinear order/rate) of sequences and we show that actually there are four distinct classes of strict superlinear order: “weak”, “medium”, “strong” and “mixed”. The speed of the sequences from the first three classes is increasingly much faster, term-by-term big Oh, i.e.,
\[|x^\ast-x_k|=\mathcal{O}(|y^\ast-y_k|^{\alpha}), \mbox{ as } k\rightarrow \infty, \forall \alpha>1 \mbox{ given},
\]whereas the speed of the “mixed” class cannot be assessed.

We prove that the speed of the sequences from the “medium” and “weak” classes is term-by-term slower than the speed of the sequences with high classical C-orders $p>1$ (in the sense of big Oh above), while an example shows that certain sequences from the “mixed” class may be term-by-term faster than some sequences with infinite C-order.

We also show that for a given sequence with strict superlinear convergence, one can evaluate numerically to which class it belongs.

Some recent results of Rodomanov and Nesterov (Math. Program., 2022), resp. Ye et al. (Math. Program., 2023) show that certain classical quasi-Newton methods (DFP, BFGS and SR1) belong to the “weak” class.

Authors

Emil Cătinaş
“Tiberiu Popoviciu” Institute of Numerical Analysis

Keywords

convergent sequence, convergence order, convergence speed, superlinear order, Q-order, convergence rate, big Oh, quasi-Newton method, DFP, BFGS, SR1.

Paper coordinates

E. Cătinaş, The strict superlinear order can be faster than the infinite order, Numer. Algor., 95 (2024), pp. 1177–1186. https://doi.org/10.1007/s11075-023-01604-y

PDF

https://link.springer.com/content/pdf/10.1007/s11075-023-01604-y.pdf?pdf=button

About this paper

Journal

Numerical Algorithms

Publisher Name

Springer Nature

DOI

https://doi.org/10.1007/s11075-023-01604-y

Print ISSN

1017-1398

Online ISSN

1572-9265

google scholar link

Paper (preprint) in HTML version

The strict superlinear order can be faster than the infinite order

The strict superlinear order
can be faster than the infinite order

Emil Cătinaş¹¹1“Tiberiu Popoviciu” Institute of Numerical Analysis, Romanian Academy, P.O. Box 68-1, Cluj-Napoca, 400110, Romania, e-mail: ecatinas@ictp.acad.ro.

Abstract

The sequences with strict superlinear convergence are the output of numerous algorithms; such speed is clearly much faster than linear, but is it also slower than, say, quadratic?

In this note we show that actually there are four distinct classes of strict superlinear order: “weak”, “medium”, “strong” and “mixed”. The speed of the sequences from the first three classes is increasingly much faster (term-by-term big Oh, i.e., $|x^{\ast}-x_{k}|=\mathcal{O}(|y^{\ast}-y_{k}|^{\alpha})$ , as $k\rightarrow\infty,\forall\alpha>1$ given), whereas the speed of the “mixed” class cannot be assessed.

We prove that the speed of the sequences from the “medium” and “weak” classes is term-by-term slower than the speed of the sequences with high classical $C$ -orders $p>1$ (in the sense of big Oh above), while an example shows that certain sequences from the “mixed” class may be term-by-term faster than some sequences with infinite $C$ -order.

We also show that for a given sequence with strict superlinear convergence, one can evaluate numerically to which class it belongs.

Some recent results of Rodomanov and Nesterov (2022), resp. Qi et al. (2023) show that certain classical quasi-Newton methods (DFP, BFGS and SR1) belong to the “weak” class.

Keywords: convergent sequence, convergence order, convergence speed, superlinear order, $Q$ -order, convergence rate, big Oh, quasi-Newton method, DFP, BFGS, SR1.

MSC: 40A05.

1 Introduction

We consider here real sequences $\{x_{k}\}$ converging to finite limits, $x_{k}\rightarrow x^{\ast}\in\mathbb{R}$ and, since we analyze the behavior of the absolute value of their errors, we assume without loss of generality that $x^{\ast}=0$ and $x_{k}>0$ (i.e., $x_{k}=|x^{\ast}-x_{k}|$ ). A more general frame may be considered (normed or metric spaces), but the one-dimensional setting is enough to analyze some essential properties.

First we recall some definitions and notations regarding orders other than superlinear. The quotient convergence factors are defined by [12, sect. 9.1]

Q_{p}(k):=\frac{|x^{\ast}-x_{k+1}|}{|x^{\ast}-x_{k}|^{p}}=\frac{x_{k+1}}{(x_{k% })^{p}},\quad k=0,1,\ldots,\ (p\geq 1),

with their lower/upper limits given by $\stackunder[1.2pt]{$Q$}{\rule{3.44444pt}{0.32289pt}}_{p}=\liminf\limits_{k% \rightarrow\infty}Q_{p}(k)$ , resp. $\bar{Q}_{p}=\limsup\limits_{k\rightarrow\infty}Q_{p}(k)$ [1].

The sequence $\{x_{k}\}$ has $C$ -order $p_{0}>1$ if $Q_{p_{0}}:=\lim_{k\rightarrow\infty}Q_{p_{0}}(k)\in(0,+\infty)$ (i.e., $Q_{p_{0}}$ exists and is finite and nonzero), the linear $C$ -order is attained when $Q_{1}:=\lim_{k\rightarrow\infty}Q_{1}(k)\in(0,1)$ , while the sublinear $C$ -order requires $Q_{1}=1$ .

For the $Q$ -order $p_{0}>1$ there are four equivalent definitions (see [5], [15], [1], [7], [10]), but we consider here only two convenient ones

	$\displaystyle\lim_{k\rightarrow\infty}Q_{L}(k)$	$\displaystyle=p_{0},\quad\text{with }Q_{L}(k):=\frac{\ln x_{k+1}}{\ln x_{k}},% \quad k\geq 0,$		( $Q_{L}$ )
	$\displaystyle\lim_{k\rightarrow\infty}Q_{\Lambda}(k)$	$\displaystyle=p_{0},\quad\text{ with }Q_{\Lambda}(k):=\frac{\ln\frac{x_{k+2}}{% x_{k+1}}}{\ln\frac{x_{k+1}}{x_{k}}},\quad k\geq 0.$		( $Q_{\Lambda}$ )

The lower/upper $Q$ -orders, denoted by $q_{l}$ resp. $q_{u}$ , are (see [1], [7] and [10])

q_{l}=\inf\{p\in[1,\infty)\,:\,\bar{Q}_{p}=+\infty\},\quad\mbox{resp., \quad}q% _{u}=\sup\big{\{}p\in[1,\infty):\stackunder[1.2pt]{Q}{\rule{3.44444pt}{0.32289% pt}}_{p}=0\big{\}},

and it holds:

•

$q_{l}=\liminf Q_{L}(k)$ , $q_{u}=\limsup Q_{L}(k)$ (retrieving $q_{l}\leq q_{u}$ in another way),
•

( $Q_{L}$ ) $\Leftrightarrow$ ( $Q_{\Lambda}$ ) $\Leftrightarrow p_{0}=q_{l}=q_{u}>1$ ,

the condition $p_{0}=q_{l}=q_{u}>1$ providing the third equivalent definition of the $Q$ -order $p_{0}>1$ . When $p_{0}=1$ , the four definitions are no longer equivalent, as shown in [1].

Remark 1

$Q_{1}\in[0,1]$ , when the limit exists (i.e., $Q_{1}>1$ cannot hold). When $\nexists Q_{1}$ (and therefore $\stackunder[1.2pt]{$Q$}{\rule{3.44444pt}{0.32289pt}}_{1}<\bar{Q}_{1}$ ) the “global speed” of $\{x_{k}\}$ may be difficult to assess.

The sequences with $\bar{Q}_{1}=\infty$ , called in [10] “with unbounded nonmonotone errors”³³3Recall that one cannot have $Q_{1}=+\infty$ (as suggested by a typo in the abstract of [10]), but just $\bar{Q}_{1}=+\infty$ . despite not attaining $Q$ -linear order, were shown that sometimes may have fast speed, as, e.g., $x_{k}=\Big{\{}\begin{smallmatrix}2^{-4^{k}},&k\ {\it even},\\ 2^{-5^{k}},&k\ {\it odd}\end{smallmatrix}$ $y_{k}=\Big{\{}\begin{smallmatrix}2^{-3^{2^{k}}},&k\ {\it even},\\ 2^{-4^{2^{k}}},&k\ {\it odd}\end{smallmatrix}$ (see [10, Ex. 2.46]). Such sequences were also called subsequently there “with no $Q$ -order” [10, §2.2] but we notice here that such terminology is not suitable: $z_{k}=\Big{\{}\begin{smallmatrix}\frac{1}{k},\ k\text{ even}\\ \frac{1}{k\ln{k}},\ k\text{ odd}\end{smallmatrix}$ shows that one may have $\bar{Q}_{1}=\infty$ and ( $Q_{L}$ )-order one.

As regarding the fast speed, it cannot be attained when $\stackunder[1.2pt]{$Q$}{\rule{3.44444pt}{0.32289pt}}_{1}>0$ (due to the obvious lower bounds of the errors) and one necessarily needs $\stackunder[1.2pt]{$Q$}{\rule{3.44444pt}{0.32289pt}}_{1}=0$ ; however, condition $\stackunder[1.2pt]{$Q$}{\rule{3.44444pt}{0.32289pt}}_{1}=0$ alone is not also sufficient for fast speed: take $\{z_{k}\}$ above or $u_{k}=\Big{\{}\begin{smallmatrix}\frac{1}{k},\ k\text{ even}\\ \frac{1}{\sqrt{k}},\ k\text{ odd.}\end{smallmatrix}$

The $Q$ -superlinear convergence—which we call here simply as superlinear—requires (see [12, ch. 9], [4], [14], [7], [10])

\lim_{k\rightarrow\infty}\frac{x_{k+1}}{x_{k}}=0

(1)

and it is usually understood as “at least superlinear order”: indeed, all $\{x_{k}\}$ with $Q$ -order $p_{0}=q_{l}=q_{u}>1$ or just with lower $Q$ -order $q_{l}>1$ are also superlinear ( $q_{l}>1$ implies $\forall p\in(1,q_{l}),\exists A>0$ s.t. $x_{k+1}<A\cdot{x_{k}}^{p}$ , $k\geq 0$ [12, sect. 9.1], [10] and therefore $\frac{x_{k+1}}{x_{k}}<A\cdot x_{k}^{p-1}\rightarrow 0$ ).

Remark 2

There is another type of superlinear speed, the $R$ -superlinear order, usually defined by using root-convergence factors (see [12, ch. 9], [14]), or (as for higher orders), simply by requiring that the errors are bounded by another sequence, converging to zero with $Q$ -superlinear order [19], [13, (37b)].

Tapia [19] noticed that convergence with (lower) $R$ -order $p_{0}$ arbitrary high does not imply $Q$ -superlinear convergence, while Boggs, Tolle and Wang [3] concluded that “because an $R$ -superlinearly convergent sequence need not be even $Q$ -linearly convergent, $R$ -superlinear convergence by itself is computationally meaningless”. We have seen in the previous Example that the fast sequence $\{y_{k}\}$ with $R$ -superlinear convergence (in fact with infinite $R$ -order) not only that does not attain some type of $Q$ -linear order, but even has unbounded nonmonotone errors ( $\bar{Q}_{1}=\infty$ ).

The above Example therefore shows that the $Q$ -superlinear convergence is not necessary for high speed: $\{y_{k}\}$ there converges pretty fast despite $\bar{Q}_{1}=+\infty$ .

2 The strict superlinear (SSL) convergence

The strict superlinear (SSL) convergence requires additionally that [10]

\bar{Q}_{p}=\limsup_{k\rightarrow\infty}\frac{x_{k+1}}{{x_{k}}^{p}}=+\infty,\;% \;\;\forall p>1,

(2)

i.e., $\{x_{k}\}$ does attain neither some $Q$ -order $p_{0}>1$ nor some lower $Q$ -order $q_{l}>1$ .

The SSL was usually seen as a fast convergence, with an intermediate speed between the linear and high orders. Indeed, the SSL is (much) faster than the linear $C$ -order, in the sense that

x_{k}=\mathcal{O}(y_{k}^{\alpha}),\text{ as }k\rightarrow\infty\ (\forall% \alpha>1\text{ given}).

(

x_{k}={\mathcal{O}}(y_{k}^{\alpha})

)

Proposition 3

If $\{x_{k}\}$ has SSL order and $\{y_{k}\}$ has $C$ -linear order then $\{x_{k}\}$ is $[$ ( $x_{k}={\mathcal{O}}(y_{k}^{\alpha})$ ), $\forall\alpha>1]$ faster than $\{y_{k}\}$ .

For the proof we use here (and later too) the well known ratio test for sequences.

Lemma 4

Given a sequence $\{z_{k}\}\subset{\mathbb{R}}$ with $z_{k}>0$ $k\geq 0$ , if $\frac{z_{k+1}}{z_{k}}\rightarrow 0$ then $z_{k}\rightarrow 0$ . The same conclusion holds if $\frac{z_{k+1}}{z_{k}}\rightarrow q\in(0,1)$ .

Proof of Proposition 3. Take $z_{k}=\frac{x_{k}}{y_{k}^{\alpha}}$ and apply Lemma 4.

However, the SSL convergence is not always slower than that with some $Q$ -order $p_{0}>1$ , as we will show in Example 10. Before that, we further analyze the SSL order.

Example 5

The convergence of $\{\frac{1}{k!}\}$ and of $\{\frac{1}{k^{k}}\}$ is SSL—with the “strictness” implied by their $Q_{\Lambda}$ -order one ( $Q_{\Lambda}(k)\rightarrow 1$ ).

By denoting $a_{0}=x_{0}$ , $a_{k+1}=\frac{x_{k+1}}{x_{k}}>0$ , $k\geq 0,$ ⁴⁴4When $\{x_{k}\}$ is starting from $x_{1}$ , $\{a_{k}\}$ is starting from $a_{1}$ (as, e.g., $\{\frac{1}{k^{k}}\}$ , $\{\frac{1}{k}\}$ , etc.). condition (1) may be equivalently written as (see, e.g., [13, (37b)] and [10])

x_{k}=\textstyle\prod\limits_{i=0}^{k}a_{i},\;\;\;\text{with }a_{k}\rightarrow 0% ,\text{ as }k\rightarrow\infty.

(3)

For the SSL convergence of $\{x_{k}\}$ , the $Q$ -order of $\{a_{k}\}$ cannot be greater than one.

Theorem 6

Let $a_{k}>0$ with $a_{k}\rightarrow 0$ as $k\rightarrow\infty$ . If $\{a_{k}\}$ has $Q_{L}$ -order $p_{0}=1,$ then $\{x_{k}\}$ from (3) has SSL order. If $\{a_{k}\}$ has $Q$ -order $p_{0}>1,$ then $\{x_{k}\}$ has $Q$ -order $p_{0}.$

Proof. The proof is obtained by using ( $Q_{\Lambda}$ ).

Now, consider $\{a_{k}\}$ , or just simply ask ourselves: how fast does $\{\frac{x_{k+1}}{x_{k}}\}$ converge to zero? We obtain the following classification of the SSL order:

(a) (strong SSL): $a_{k}\rightarrow 0$ strict superlinearly: $\lim\limits_{k\rightarrow\infty}\frac{a_{k+1}}{a_{k}}=\lim\limits_{k% \rightarrow\infty}\frac{x_{k+1}x_{k-1}}{x_{k}^{2}}=0;$
(b) (medium SSL): $a_{k}\rightarrow 0$ with $C$ -order $1$ : $\lim\limits_{k\rightarrow\infty}\frac{a_{k+1}}{a_{k}}=\lim\limits_{k% \rightarrow\infty}\frac{x_{k+1}x_{k-1}}{x_{k}^{2}}=q\in(0,1);$
(c) (weak SSL): $a_{k}\rightarrow 0$ $C$ -sublinearly: $\lim\limits_{k\rightarrow\infty}\frac{a_{k+1}}{a_{k}}=\lim\limits_{k% \rightarrow\infty}\frac{x_{k+1}x_{k-1}}{x_{k}^{2}}=1;$
(d) (mixed SSL): otherwise.

Remark 7

We note that the weak SSL order may be defined by requiring only that $0<\bar{Q}_{1}<1$ (instead of requiring $C$ -linear order).

Example 8

One can show that $\{\frac{1}{2^{k^{2}}}\}$ has medium SSL while $\{\frac{1}{2^{k^{3}}}\}$ has strong SSL order.

Example 9

$\{\frac{1}{k^{k}}\}$ has weak SSL order (hint: $a_{k+1}=\frac{1}{k+1}\frac{1}{(1+\frac{1}{k})^{k}}\approx\frac{1}{e}\cdot\frac% {1}{k+1}$ ).

Example 10

a) (strong SSL) $a_{k}=\frac{1}{k!},$ so $x_{k}=\frac{1}{1!2!\cdot\ldots\cdot k!}$ ; one may take further $b_{k}=\frac{1}{1!2!\cdot\ldots\cdot k!}$ and by theorem 6 $y_{k}=b_{1}\ldots b_{k}$ is again SSL, etc. For another instance, take $c_{k}=\frac{1}{k^{k}}$ , so $z_{k}=\frac{1}{1^{1}\cdot 2^{2}\cdots k^{k}},etc.;$

b) (medium SSL) for $q\in\left(0,1\right)$ fixed, take $a_{k}=q^{k},$ so $x_{k}=q^{1}\cdot\ldots\cdot q^{k}=q^{\frac{k\left(k+1\right)}{2}};$

c) (weak SSL) $a_{k}=\frac{1}{k}$ , so $x_{k}=\frac{1}{k!};$

For the mixed class, we may take (similar) sequences from Remark 1 as $\{a_{k}\}$ .

d) (mixed SSL) $a_{k}=\Big{\{}\begin{smallmatrix}\frac{1}{2^{2^{k}}},\ k\text{ even}\\ \frac{1}{2^{3^{k}}},\ k\text{ odd,}\end{smallmatrix}$ $b_{k}=\Big{\{}\begin{smallmatrix}\frac{1}{2^{2^{2^{k}}}},\ k\text{ even}\\ \frac{1}{2^{3^{2^{k}}}},\ k\text{ odd,}\end{smallmatrix}$ $c_{k}=\Big{\{}\begin{smallmatrix}\frac{1}{k},\ k\text{ even}\\ \frac{1}{k\ln k},\ k\text{ odd,}\end{smallmatrix}$ $d_{k}=\Big{\{}\begin{smallmatrix}\frac{1}{\sqrt{k}},\ k\text{ even}\\ \frac{1}{(\ln k)\sqrt{k}},\ k\text{ odd,}\end{smallmatrix}$ etc., resulting the corresponding sequences $\{x_{k}\}$ , $\{y_{k}\}$ , $\{z_{k}\}$ , resp. $\{u_{k}\}$ .

We notice that $y_{k}<b_{k}\leq\frac{1}{2^{2^{2^{k}}}}$ , $k\geq 1$ , i.e., the SSL $\{y_{k}\}$ is term-by-term faster than $\{b_{k}\}$ (with no $Q$ -order) which is in turn term-by-term faster than $\{\frac{1}{2^{2^{2^{k}}}}\}$ (with infinite $C$ - and $Q$ -order).

In Figure 1 we have plotted some of these sequences ( $k\geq 1$ ), computed using the Tikz/Pgf LaTeX package [18] (the cases $\{x_{k}\}$ , $\{z_{k}\}$ from (a), $\{x_{k}\}$ from (c) and $\{x_{k}\}$ , $\{y_{k}\}$ from (d), were first computed in Julia [2], using BigFloat with setprecision(10^4), and then passed to Tikz/Pgf).

The first values of the fastest sequence (in red), written truncated, are $x_{0}=\numprint{2.5e-1}$ (not plotted), $x_{1}=\numprint{4.8e-4}$ , $x_{2}=\numprint{7.4e-9}$ , $x_{3}=\numprint{6.5e-1984}$ , $x_{4}=\numprint{3.2e-21712}$ , and $x_{4}$ cannot therefore be plotted, being below the realmin $\approx 10^{-7100}$ from Tikz/Pgf.

The second fastest sequence (violet, with infinite $C$ -order) has the following iterates $x_{0}=\numprint{2.5e-1}$ (not plotted), $x_{1}=\numprint{6.2e-2}$ , $x_{2}=\numprint{1.5e-5}$ , $x_{3}=\numprint{8.6e-78}$ , $x_{4}=\numprint{4.9e-19729}$ (not plotted).

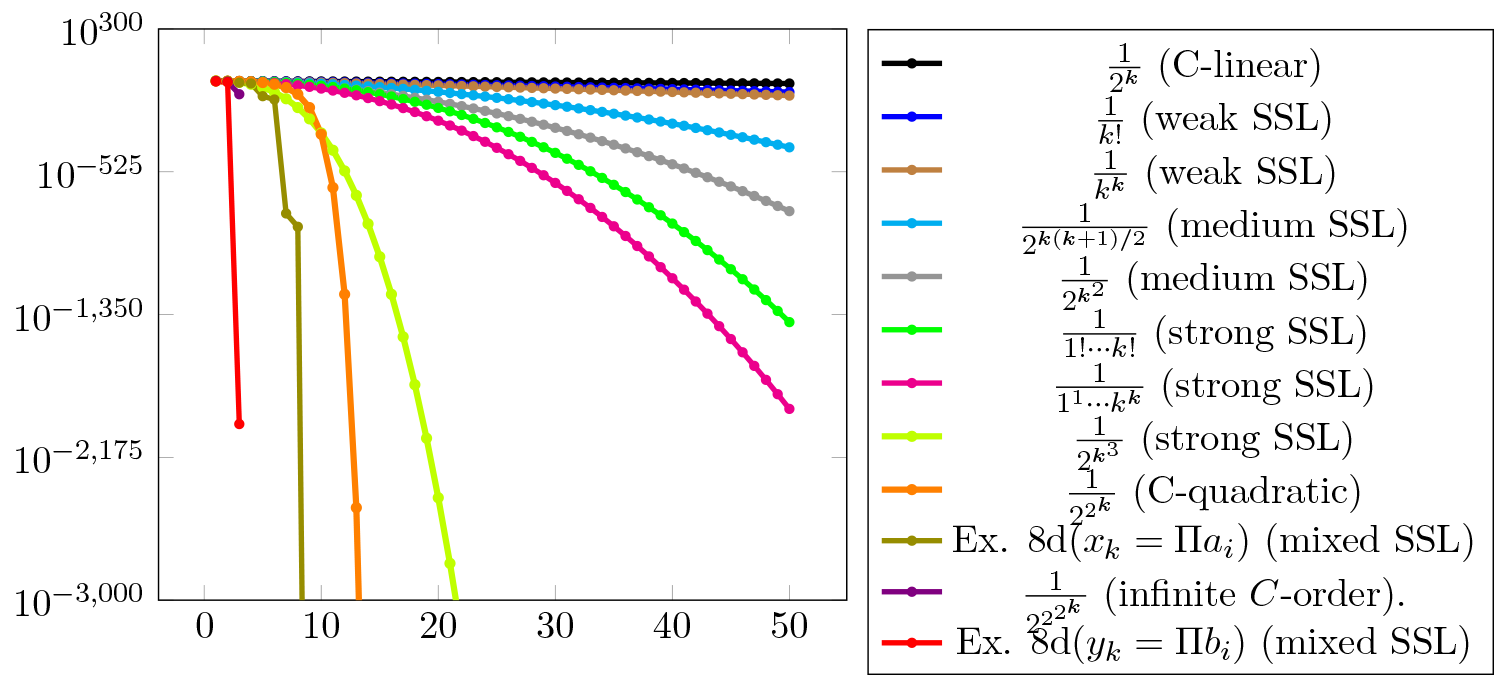
Refer to caption — Figure 1: Linear, weak SSL, medium SSL, strong SSL, mixed SSL, quadratic and infinite orders.

The strong SSL $\{\frac{1}{2^{k^{3}}}\}$ appears close to the quadratic $\{\frac{1}{2^{2^{k}}}\}$ , but their speed is quite different (as also shown by the next Theorem): indeed, at $k=11$ , $\{\frac{1}{2^{2^{k}}}\}$ has approximately the same value as $\{\frac{1}{2^{k^{3}}}\}$ at $k=16$ ; one more step of $\{\frac{1}{2^{2^{k}}}\}$ needs four steps of $\{\frac{1}{2^{k^{3}}}\}$ to get the same magnitude.

With the scales of Figure 1, the weak SSL of $x_{k}=\frac{1}{k!}$ appears only slightly faster than that of the linear $\{\frac{1}{2^{k}}\}$ , but the conclusions of Proposition 3 hold.

The following result justifies the terminology of strong, medium and weak SSL.

Theorem 11

If $\{x_{k}\}$ has strong SSL and $\{y_{k}\}$ has medium SSL, then $\{x_{k}\}$ is $[$ ( $x_{k}={\mathcal{O}}(y_{k}^{\alpha})$ ), $\forall\alpha>1]$ faster than $\{y_{k}\}$ . The same conclusion holds for $\{x_{k}\}$ with medium SSL and $\{y_{k}\}$ with weak SSL order.

Proof. Let $x_{k}=\prod\limits_{i=0}^{k}a_{i},\ y_{k}=\prod\limits_{i=0}^{k}b_{i},$ with $\lim\frac{a_{k+1}}{a_{k}}=0$ and $\lim\frac{b_{k+1}}{b_{k}}=q\in(0,1)$ .

As $\Big{(}\frac{x_{k+1}}{x_{k}}/\frac{x_{k}}{x_{k-1}}\Big{)}\Big{/}\Big{(}\frac{y% _{k+1}}{y_{k}}/\frac{y_{k}}{y_{k-1}}\Big{)}^{\alpha}=\frac{a_{k+1}}{a_{k}}\big% {/}\big{(}\frac{b_{k+1}}{b_{k}}\big{)}^{\alpha}\rightarrow 0$ , by Lemma 4 we get $\frac{x_{k+1}}{x_{k}}\big{/}\big{(}\frac{y_{k+1}}{y_{k}}\big{)}^{\alpha}\rightarrow 0$ and therefore $\frac{x_{k}}{y_{k}^{\alpha}}\rightarrow 0$ . The second part is similar.

Remark 12

In [10, Rem. 2.50(b)] we noted (without proof) that “the $C$ -orders (i.e., sublinear, linear, strict superlinear, $1<\mathring{p}_{0}<\dot{p}_{0}$ and infinite) form classes in $[$ ( $x_{k}={\mathcal{O}}(y_{k}^{\alpha})$ ), $\forall\alpha>1]$ increasing speed”. However, the SSL order was erroneously mentioned, as it is not a $C$ -order (its definition requires $\bar{Q}_{p}$ , as noted in (2)) and moreover such a statement does not hold, as we have already seen in Example 10.

Here we prove that the weak and the medium SSL are (much) slower than the $C$ -orders $p>1$ .

Theorem 13

If $\{x_{k}\}$ has $C$ -order $p_{0}>1$ and $\{y_{k}\}$ has weak or medium SSL then $\{x_{k}\}$ is $[$ ( $x_{k}={\mathcal{O}}(y_{k}^{\alpha})$ ), $\forall\alpha>1]$ faster than $\{y_{k}\}$ .

Proof. Let $u_{k}=\frac{x_{k}}{y_{k}^{\alpha}}$ , $v_{k}=\frac{u_{k+1}}{u_{k}}$ . As $\frac{v_{k+1}}{v_{k}}=\frac{x_{k+2}}{x_{k+1}^{p_{0}}}\frac{x_{k}^{p_{0}}}{x_{k% +1}}\big{(}\frac{x_{k+1}}{x_{k}}\big{)}^{p_{0}-1}\big{(}\frac{y_{k+1}^{2}}{y_{% k}y_{k+2}}\big{)}^{\alpha}\rightarrow 0$ , by Lemma 4 we successively get $v_{k},u_{k}\rightarrow 0$ .

In some particular cases, the strong SSL is also (much) slower than $C$ -order $p>1$ .

Theorem 14

Let $\{x_{k}\}$ have $C$ -order $p>1$ and $\{y_{k}\}$ have strong SSL order: $b_{k}=\frac{a_{k+1}}{a_{k}}\rightarrow 0$ , $a_{k}=\frac{y_{k+1}}{y_{k}}$ . If $\{b_{k}\}$ has weak or medium SSL then $\{x_{k}\}$ is $[$ ( $x_{k}={\mathcal{O}}(y_{k}^{\alpha})$ ), $\forall\alpha>1]$ faster than $\{y_{k}\}$ .

Proof. The proof is similar to the one of Theorem 13.

For the remaining part of this paper we denote the absolute value of errors by $|x^{\ast}-x_{k}|$ (instead of simply by $x_{k}$ ).

In case of at least superlinear convergence, it was shown that the absolute value of the errors $|x^{\ast}-x_{k}|$ and of the corrections $|x_{k+1}-x_{k}|$ behave asymptotically in the same way (the result also holds in ${\mathbb{R}}^{N}$ ).

Lemma 15 (Potra–Pták Lemma, [14, Prop. 6.4]; see also [20])

$x_{k}\rightarrow x^{\ast}\in{\mathbb{R}}$ at least $Q$ -superlinearly iff $x_{k+1}-x_{k}\rightarrow 0$ at least $Q$ -superlinearly.

If $\{x_{k}\}$ has (at least) $Q$ -superlinear convergence, then it holds that (the Dennis–Moré Lemma [11])

\lim_{k\rightarrow\infty}\tfrac{|x_{k+1}-x_{k}|}{|x^{\ast}-x_{k}|}=1.

(4)

We obtain the following immediate result, which holds in ${\mathbb{R}}^{N}$ as well.

Corollary 16

Given a sequence $\{x_{k}\}\subset{\mathbb{R}}$ s.t. $x_{k}\rightarrow x^{\ast}\in{\mathbb{R}}$ with SSL convergence, let $\alpha_{k}:=\frac{|x_{k+2}-x_{k+1}|}{|x_{k+1}-x_{k}|}$ and take

\frac{\alpha_{k+1}}{\alpha_{k}}=\frac{|x_{k+2}-x_{k+1}|\cdot|x_{k}-x_{k-1}|}{|% x_{k+1}-x_{k}|^{2}}.

(5)

•

If $\tfrac{\alpha_{k+1}}{\alpha_{k}}\rightarrow 1$ then $\{x_{k}\}$ has weak SSL;
•

if $\tfrac{\alpha_{k+1}}{\alpha_{k}}\rightarrow q\in(0,1)$ then $\{x_{k}\}$ has medium SSL;
•

if $\tfrac{\alpha_{k+1}}{\alpha_{k}}\rightarrow 0$ then $\{x_{k}\}$ has strong SSL;
•

if $\{\tfrac{\alpha_{k+1}}{\alpha_{k}}\}$ does not converge at all then $\{x_{k}\}$ has mixed SSL.

The proof is obvious, as the errors from the expressions $\frac{a_{k+1}}{a_{k}}=\frac{|x_{k+1}-x^{\ast}|\cdot|x_{k-1}-x^{\ast}|}{|x_{k}-% x^{\ast}|^{2}}$ by (4) may be replaced by corrections.

Example 17

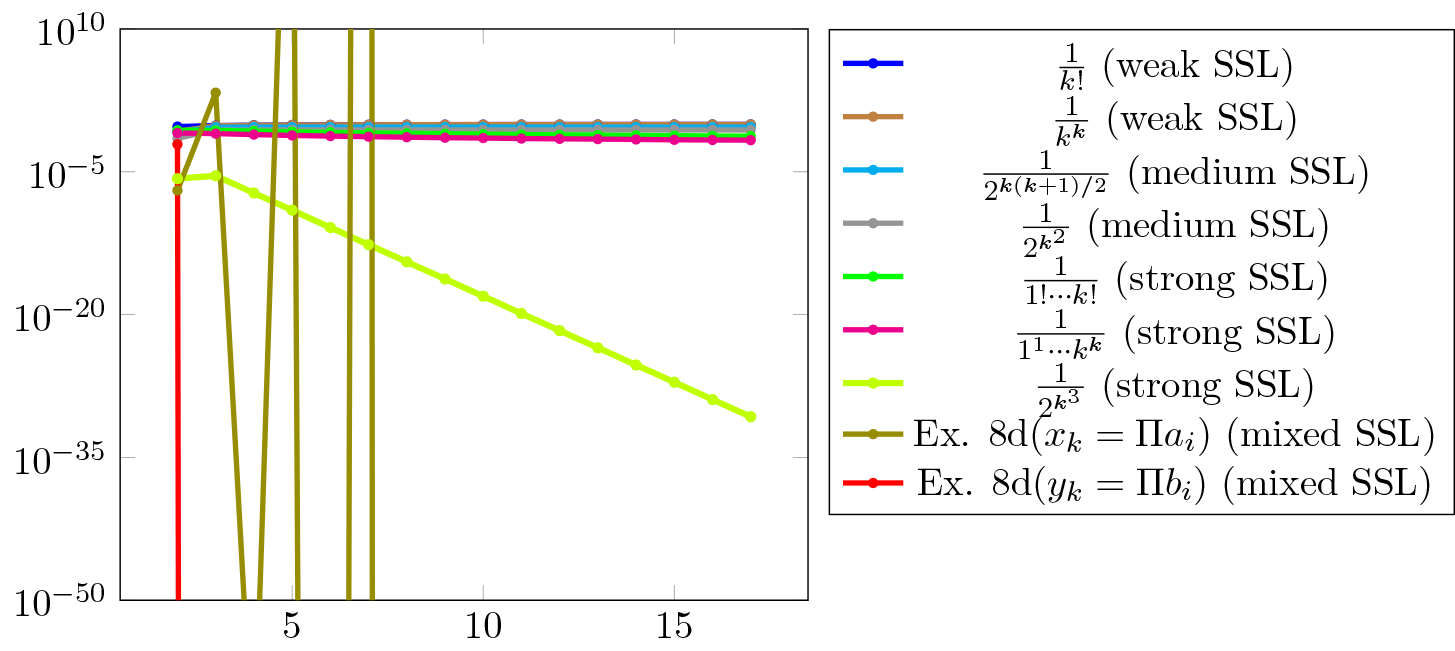
We consider the SSL sequences from Example 10 and for each of them we represent graphically in Figure 2 the expressions (5), using the same corresponding colors as in Figure 1 (here the limit $x^{\ast}=0$ is known, but formula (5) does not require its knowledge).

For the same precision as in Example 10 (setprecision(10^4)), we have obtained nonzero results for $k\leq 17$ ; the (truncated) values of $\tfrac{\alpha_{k+1}}{\alpha_{k}}$ for $k=17$ are, for the following $\{x_{k}\}$ ’s: $\{\frac{1}{k^{k}}\}$ $0.943$ (true limit $1$ ); $\{\frac{1}{k!}\}$ $0.944$ (true limit $1$ ); $\{\frac{1}{2^{k(k+1)/2}}\}$ $0.4999990$ (true limit $\frac{1}{2}$ ); $\{\frac{1}{2^{k^{2}}}\}$ $0.2499999$ (true limit $\frac{1}{4}$ ); $\{\frac{1}{1!\cdots k!}\}$ $0.055$ (true limit $0$ , but very slow convergence); $\{\frac{1}{1^{1}\cdots k^{k}}\}$ $0.0210$ (true limit $0$ , but very slow convergence); $\{\frac{1}{2^{k^{3}}}\}$ $\numprint{1.97e-31}$ (true limit $0$ ).

In the last two cases (Example 10d, $x_{k}=\Pi a_{i}$ , resp. $y_{k}=\Pi b_{i}$ ), much fewer relevant terms can be computed with this precision, and one clearly see we do not have convergence.

In each case it is confirmed numerically that the sequence belongs to the stated SSL class. However, it is worth noting that in some cases (e.g., $\{\frac{1}{1!\cdots k!}\}$ and $\{\frac{1}{1^{1}\cdots k^{k}}\}$ ) some more terms are needed to conclude that the sequence $\{\tfrac{\alpha_{k+1}}{\alpha_{k}}\}$ converges.

In certain applications it may be difficult to verify numerically whether $\tfrac{\alpha_{k+1}}{\alpha_{k}}$ converges to $0$ , to $1$ or to some value in $(0,1)$ (if at all), especially when the convergence is slow.

Numerous methods from Computational Optimization were proved to be with (at least) superlinear order. Three classical methods have explicit expressions for their errors, and now their speed can be assessed.

Example 18

The quasi-Newton methods for smooth unconstrained optimization are known for a long time that attain superlinear order, but it is only recently that some explicit expressions for the errors have been obtained.

Rodomanov and Nesterov [16] have shown for the Davidon–Fletcher–Powell (DFP) method that the errors are of the form $e_{k}=(\frac{a}{k})^{\frac{k}{2}}$ ( $a$ depending on the dimension problem, the Lipschitz constant and the strong convexity parameter) and for the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method that similarly $e_{k}=(\frac{b}{k})^{\frac{k}{2}}$ .

Subsequently, Ye et al. [21] have shown for the Symmetric-Rank 1 (SR1) method that $e_{k}=(\frac{c}{k})^{\frac{k}{2}}$ .

We see that all the three methods attain weak SSL order, and it becomes interesting to find methods with medium or perhaps strong SSL order, for the reason that their faster speed may appear from the first terms.

3 Conclusions

The main role of the convergence orders is to allow the comparison of the speed of different convergent sequences: we usually expect that the higher the order, the faster the speed; while this is in general true (as shown in [8] for orders $1<p<q<+\infty$ ), these notions are imperfect and there are some notable exceptions. Indeed, a sequence with no $Q$ -order was shown in [10] that may have fast speed (term-by-term faster than another sequence, with infinite order).

Here we have seen that a similar phenomenon holds in the case of the (mixed) superlinear convergence, as such a sequence may converge faster than another sequence, with infinite order (though, it is worth noting that not all sequences with mixed SSL order have such fast speed).

The explanation for such a behavior resides in the fact that both the superlinear and the $Q$ -orders rely on conditions on consecutive errors, not on “global” relations involving all the errors. The graph of the sequence from Example 10(d) ( $x_{k}=\Pi a_{i}$ ) which was plotted in Figure 1 in olive color is perhaps most relevant: while its speed is high (steep slope), some of the consecutive errors do not have a high relative reduction.

A similar analysis may be taken for the linear convergence [9], and the higher orders [8], but with notable different particularities; we have also started to analyze the sublinear convergence.

In [6] we study the speed of $\{Q_{\Lambda}(k)\}$ and $\{Q_{L}(k)\}$ , while in [17] we obtain some simplified proofs for the $Q$ -order.

Data availability. All data generated or analysed during this study are included in this published article.

Conflict of interest. The author has no conflict of interests to declare that are relevant to the content of this article.

Ethical Approval. Not Applicable.

Availability of supporting data. Not Applicable.

Competing interests. Not Applicable.

Funding. Not Applicable.

Authors’ contributions. Not Applicable.

Acknowledgments. Not Applicable.

References

[1] W. A. Beyer, B. R. Ebanks, and C. R. Qualls (1990) Convergence rates and convergence-order profiles for sequences. Acta Appl. Math. 20 (), pp. 267–284. External Links: Document Cited by: §1, §1, §1.
[2] J. Bezanson, A. Edelman, S. Karpinski, and V. B. Shah (2017) Julia: a fresh approach to numerical computing. SIAM Review 59 (), pp. 65–98. External Links: Document Cited by: Example 10.
[3] P. T. Boggs, J. W. Tolle, and P. Wang (1982) On the local convergence of quasi-newton methods for constrained optimization. SIAM Journal on Control and Optimization 20 (2), pp. 161–171. External Links: Document, Link, https://doi.org/10.1137/0320014 Cited by: Remark 2.
[4] C. Brezinski (1977) Accélération de la convergence en analyse numérique. Springer-Verlag, Berlin. Cited by: §1.
[5] C. Brezinski (1985) Vitesse de convergence d’une suite. Rev. Roumaine Math. Pures Appl. 30, pp. 403–417. Cited by: §1.
[6] E. Cătinaş and A. Stan (2021) Measuring the measures. Note: (manuscript) Cited by: §3.
[7] E. Cătinaş (2019) A survey on the high convergence orders and computational convergence orders of sequences. Appl. Math. Comput. 343 (), pp. 1–20. External Links: Document Cited by: §1, §1, §1.
[8] E. Cătinaş (2021) Characterizing the classical convergence orders. Note: manuscript, submitted Cited by: §3, §3.
[9] E. Cătinaş (2021) Characterizing the classical linear convergence order. Note: manuscript Cited by: §3.
[10] E. Cătinaş (2021) How many steps still left to $x$ *?. SIAM Rev. 63 (3), pp. 585–624. External Links: Document Cited by: §1, §1, §1, §2, §2, §3, Remark 1, Remark 12, footnote 3.
[11] J. E. Dennis, Jr. and J. J. Moré (1974) A characterization of superlinear convergence and its application to quasi-Newton methods. Math. Comp. 28 (126), pp. 549–560. External Links: Document Cited by: Lemma 15.
[12] J. M. Ortega and W. C. Rheinboldt (2000) Iterative solution of nonlinear equations in several variables. SIAM, PA. External Links: Document Cited by: §1, §1, Remark 2.
[13] E. Polak (1997) Optimization. algorithms and consistent approximations. Springer-Verlag, New York. Cited by: §2, Remark 2.
[14] F. A. Potra and V. Pták (1984) Nondiscrete induction and iterative processes. Pitman, Boston, Massachusetts. Cited by: §1, Lemma 15, Remark 2.
[15] F. A. Potra (1989) On Q-order and R-order of convergence. J. Optim. Theory Appl. 63 (3), pp. 415–431. External Links: Document Cited by: §1.
[16] A. Rodomanov and Y. Nesterov (2022) Rates of superlinear convergence for classical quasi-Newton methods. Math. Program. 194 (1-2, Ser. A), pp. 159–190. External Links: ISSN 0025-5610, Document, Link Cited by: Example 18.
[17] A. Stan and E. Cătinaş (2021) Simpler proofs for the Q-order. Note: manuscript Cited by: §3.
[18] T. Tantau The tikz and pgf packages. Manual for version 3.1.5b-34-gff02ccd1. External Links: Link Cited by: Example 10.
[19] R. A. Tapia (1977) Diagonalized multiplier methods and quasi-Newton methods for constrained optimization. J. Optim. Theory Appl. 22 (2), pp. 135–194. External Links: ISSN 0022-3239, Document, Link Cited by: Remark 2, Remark 2.
[20] H. F. Walker (1997) An approach to continuation using Krylov subspace methods. Computational Science in the 21st Century, J. Periaux, ed., John Wiley and Sons, Ltd., pp. 72–81. Cited by: Lemma 15.
[21] H. Ye, D. Lin, X. Chang, and Z. Zhang (2023) Towards explicit superlinear convergence rate for SR1. Math. Program. 199 (1-2, Ser. A), pp. 1273–1303. External Links: ISSN 0025-5610, Document, Link, MathReview Entry Cited by: Example 18.

[1] Ortega, J.M., Rheinboldt, W.C.: Iterative Solution of Nonlinear Equations in Several Variables. SIAM, PA (2000)
[2] Beyer, W.A., Ebanks, B.R., Qualls, C.R.: Convergence rates and convergence-order profiles for sequences. Acta Appl. Math. 20, 267–284 (1990)
[3] Brezinski, C., Vitesse de convergence d’une suite. Rev. Roumaine Math. Pures Appl. 30, 403–417 (1985)
[4] Potra, F.A., On Q-order and R-order of convergence. J. Optim. Theory Appl. 63(3), 415–431 (1989)
[5] Catinas, E., A survey on the high convergence orders and computational convergence orders of sequences. Appl. Math. Comput. 343, 1–20 (2019)
[6] Catinas, E., How many steps still left to x*? SIAM Rev. 63(3), 585–624 (2021)
[7] Brezinski, C., Accélération de la Convergence en Analyse Numérique. Springer-Verlag, Berlin (1977)
[8] Potra, F.A., Pták, V., Nondiscrete Induction and Iterative Processes. Pitman, Boston, Massachusetts (1984)
[9] Tapia, R.A., Diagonalized multiplier methods and quasi-Newton methods for constrained optimization. J. Optim. Theory Appl. 22(2), 135–194 (1977)
[10] Polak, E., Optimization. Algorithms and Consistent Approximations. Springer-Verlag, New York (1997)
[11] Boggs, Paul T., Tolle, Jon W., Wang, Pyng, On the local convergence of Quasi-Newton methods for constrained optimization. SIAM Journal on Control and Optimization 20(2), 161–171 (1982)
[12] Tantau, T., The tikz and pgf packages. Manual for version 3.1.5b-34-gff02ccd1
[13] Bezanson, J., Edelman, A., Karpinski, S., Shah, V.B.: Julia: a fresh approach to numerical computing. SIAM Review 59, 65–98 (2017)
[14] Walker, H.F., An approach to continuation using Krylov subspace methods. In: Periaux, J. (ed.) Computational Science in the 21st Century, pp. 72–81. John Wiley and Sons, Ltd. (1997)
[15] Dennis, J.E., Jr., Moré, J.J., A characterization of superlinear convergence and its application to quasiNewton methods. Math. Comp. 28(126), 549–560 (1974)
[16] Rodomanov, A., Nesterov, Y., Rates of superlinear convergence for classical quasi-Newton methods. Math. Program. 194(1–2, Ser. A), 159–190 (2022)
[17] Ye, H., Lin, D., Chang, X., Zhang, Z., Towards explicit superlinear convergence rate for SR1. Math. Program. 199(1–2, Ser. A), 1273–1303 (2023)
[18] Catinas, E., Characterizing the classical convergence orders. Manuscript, submitted (2021)
[19] Catinas, E., Characterizing the classical linear convergence order Manuscript. (2021)
[20] Catinas, E., Stan, A., Measuring the measures. (2021). (manuscript)
[21] Stan, A., Catinas, E., Simpler proofs for the Q-order. Manuscript (2021)

2024

Properties of positive linear operators connected with squared fundamental functions

11 Mar at 7:41 am

Localization of energies in Navier–Stokes models with reaction terms

16 Jul at 8:17 am

25 Mar at 7:43 am

The strict superlinear order can be faster than the infinite order

Abstract

Authors

Keywords

Paper coordinates

PDF

About this paper

Journal

Publisher Name

DOI

Print ISSN

Online ISSN

Paper (preprint) in HTML version

The strict superlinear order can be faster than the infinite order

Abstract

1 Introduction

Remark 1

Remark 2

2 The strict superlinear (SSL) convergence

Proposition 3

Lemma 4

Example 5

Theorem 6

Remark 7

Example 8

Example 9

Example 10

Theorem 11

Remark 12

Theorem 13

Theorem 14

Lemma 15 (Potra–Pták Lemma, [14, Prop. 6.4]; see also [20])

Corollary 16

Example 17

Example 18

3 Conclusions

References

References

Related Posts

The strict superlinear order
can be faster than the infinite order