Abstract
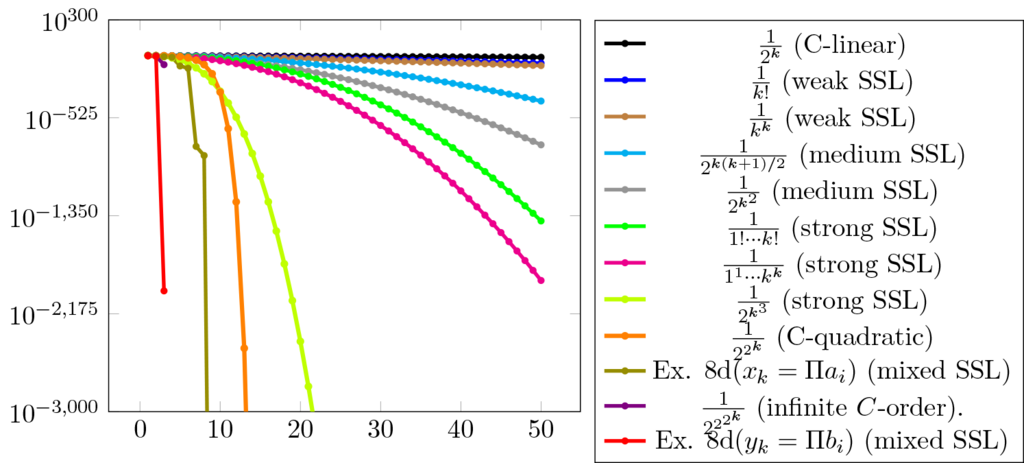
Numerical solutions for flows in partially saturated porous media pose challenges related to the non-linearity and elliptic-parabolic degeneracy of the governing Richards’ equation. Iterative methods are therefore required to manage the complexity of the flow problem. Norms of successive corrections in the iterative procedure form sequences of positive numbers. Definitions of computational orders of convergence and theoretical results for abstract convergent sequences can thus be used to evaluate and compare different iterative methods. We analyze in this frame Newton’s and L-scheme methods for an implicit finite element method (FEM) and the L-scheme for an explicit finite difference method (FDM). We also investigate the effect of the Anderson Acceleration (AA) on both the implicit and the explicit L-schemes. Considering a two-dimensional test problem, we found that the AA halves the number of iterations and renders the convergence of the FEM scheme two times faster. As for the FDM approach, AA does not reduce the number of iterations and even increases the computational effort. Instead, being explicit, the FDM L-scheme without AA is faster and as accurate as the FEM L-scheme with AA.
Authors
Nicolae Suciu
Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy
Florin A. Radu
Center for Modeling of Coupled Subsurface Dynamics, University of Bergen, Bergen, Norway
Jacob S. Stokke
Center for Modeling of Coupled Subsurface Dynamics, University of Bergen, Bergen, Norway
Emil Cătinaș
Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy
Andra Malina
Tiberiu Popoviciu Institute of Numerical Analysis, Romanian Academy
Keywords
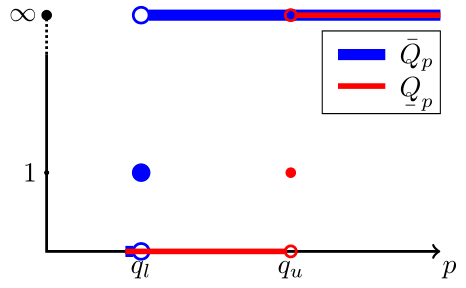
Richards’ equation; flows in partially saturated porous media; Newton’s method; L-scheme method; finite element method (FEM); finite difference method; Anderson Acceleration; computational convergence orders; Q-order; C-order; corrections; errors.
Paper coordinates
N. Suciu, F.A. Radu, J.S. Stokke, E. Cătinaș, A. Malina, Computational orders of convergence of iterative methods for Richards’ equation, arXiv:2402.00194v1, https://doi.org/10.48550/arXiv.2402.00194
About this paper
Print ISSN
Online ISSN
google scholar link
[1] Anderson, D.G., Iterative procedures for nonlinear integral equations. JACM 12(4), 547-560, (1965)
[2] Beyer, W. A., Ebanks, B. R., Qualls, C. R., Convergence rates and convergence-order profiles for sequences. Acta Appl. Math. 20, 267–284, (1990)
[3] Catinas¸, E., A survey on the high convergence orders and computational convergence orders of sequences. Appl. Math. Comput. 343, 1–20, (2019)
[4] Catinas¸, E., How many steps still left to x*? SIAM Rev. 63(3), 585–624, (2021)
[5] List, F., Radu, F.A., A study on iterative methods for solving Richards’ equation. Comput. Geosci. 20(2) 341-353, (2016)
[6] Potra, F. A., On Q-order and R-order of convergence. J. Optim. Theory Appl. 63(3), 415–431,(1989)
[7] Radu, F.A., Pop, I.S., Knabner, P., On the convergence of the Newton method for the mixed finite element discretization of a class of degenerate parabolic equations. In: Numerical Mathematics and Advanced Applications 42, 1192-1200, (2006)
[8] Suciu, N., Illiano, D., Prechtel, A., Radu, F.A., Global random walk solvers for fully coupled flow and transport in saturated/unsaturated porous media. Adv. Water Resour. 152, 103935, (2021)
[9] Suciu, N., Radu, F.A., Global random walk solvers for reactive transport and biodegradation processes in heterogeneous porous media. Adv. Water Res., 166, 104268, (2022)
[10] Stokke, J.S., Mitra, K., Storvik, E., Both, J.W., Radu, F.A., An adaptive solution strategy for Richards’ equation. Comput. Math. Appl. 152, 155-167, (2023)