Convergence order (order of convergence)

The convergence order (the order of convergence or convergence rate) are notions for measuring the convergence speed of convergent sequences \(  x_k \rightarrow x^\ast\in X\).

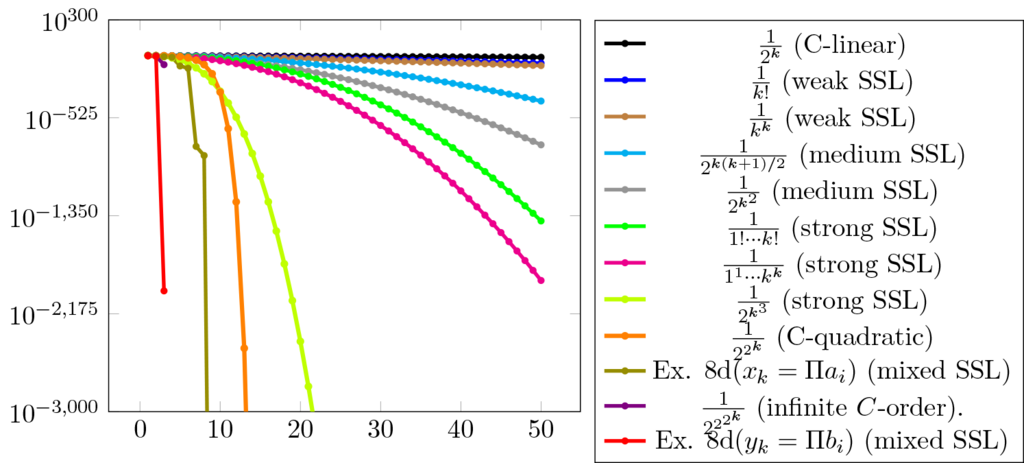
Usually, the higher the order, the faster the speed, but there are some notable exceptions. One expects that the fastest speed is achieved by the infinite order, but this is not always true: one may find sequences with no order or sequences with strict superlinear order, which which are term by term faster than some sequences with infinite order (see [Catinas, 2021] or [Catinas, 2023]).

The first survey paper on convergence orders was recently published, in [Catinas, 2019].

The convergence orders are defined using the errors \( x^\ast – x_k \). For simplicity, let \(X={\mathbb R}\) and let \( e_k: = |x^\ast – x_k| \).

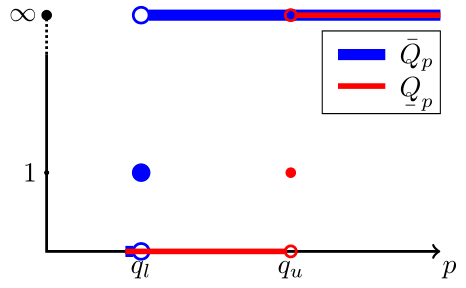
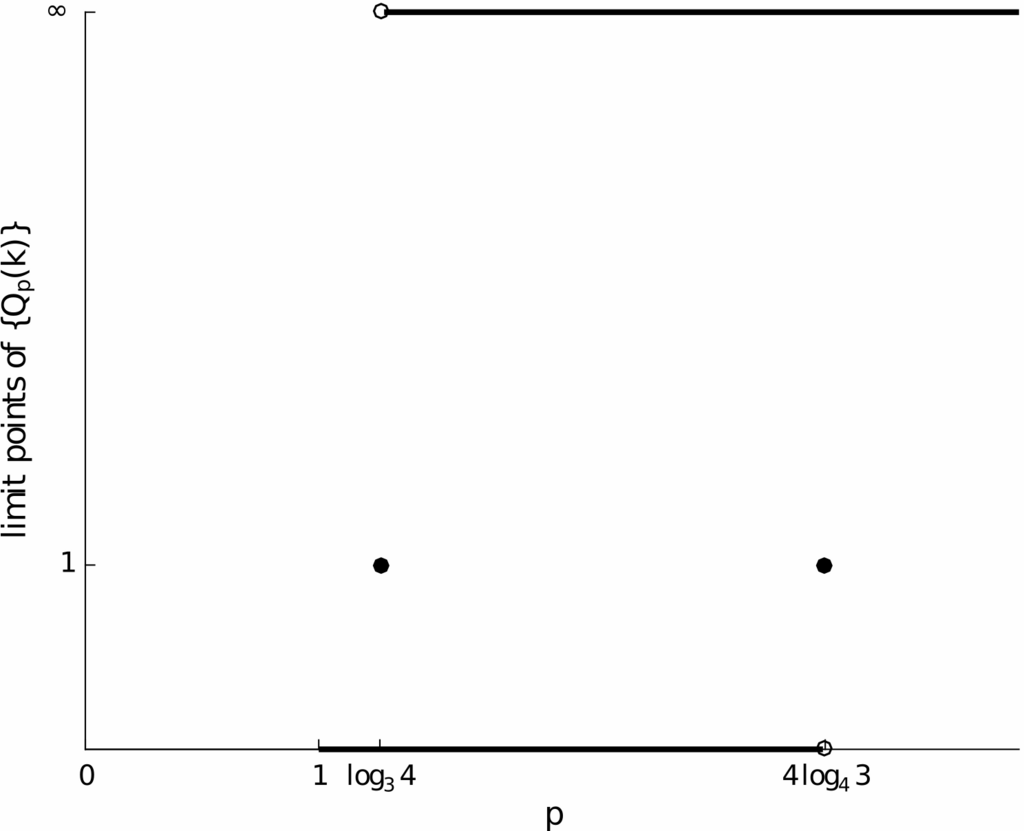
For a given \(p\geq 1\), let \(Q_p(k)=\frac{e_{k+1}}{{e_k}^p}\), \(k\geq 1\) denote the quotient convergence factors.

High convergence orders \(p_0>1\)

Three main classes exist, C (classic), Q (quotient) and R (root) convergence orders:

Classical order \(p_0>1\)

when

\[
\lim \limits_{k\rightarrow \infty} Q_{p_0}(k)=Q_{p_0}\in(0,\infty)
\qquad {\rm i.e.,}\
\lim\limits_{k\rightarrow \infty}\textstyle\frac{e_{k+1}}{e_k ^{p_0}}=\lim\limits_{k\rightarrow \infty}\frac{| x^\ast – x_{k+1}|}{| x^\ast – x_k |^{p_0}}=Q_{p_0}\in(0,\infty),
\]

Q-order \(p_0>1\)

when

\begin{equation}\tag{$Q_L$}\label{def Q_L}
\lim\limits_{k\rightarrow \infty}
\frac{\ln e_{k+1}}{\ln e_k}=p_0
\end{equation}

\(\Leftrightarrow \)

\begin{equation}\tag{$Q_\Lambda$}\label{def Q_Lam}
\lim\limits_{k\rightarrow \infty}
\frac{\ln \frac{e_{k+2}}{e_{k+1}}}{\ln \frac{e_{k+1}}{e_k}}=p_0.
\end{equation}

\(\Leftrightarrow \)
\begin{equation}\tag{$Q_Q$}\label{def Q_Q}
\begin{cases}
\lim\limits_{k\rightarrow \infty} Q_p(k)=0, & 1 \leq p < p_0 \\
\lim\limits_{k\rightarrow \infty} Q_p(k)=\infty, & p_0 < p \end{cases} \end{equation} \(\Leftrightarrow \forall \varepsilon>0,  \exists A,B\geq 0, \ k_0 \geq 0\) s.t.
\begin{equation}\tag{$Q_\varepsilon$}\label{f. def Q_eps}
A\cdot e_k ^{p_{0}+\varepsilon}\leq e_{k+1} \leq B\cdot e_k^{p_{0}-\varepsilon},\  \; \; \forall k\geq k_0
\end{equation}

R-order \(p_0>1\)

when

\begin{equation}\tag{$R_R$}\label{def R_R}
\begin{cases}
\lim\limits_{k\rightarrow \infty} e_k^{1/p^k}=0, & 1\leq p<p_0, \\ \lim\limits_{k\rightarrow \infty} e_k^{1/p^k}=1, & p_0<p
\end{cases} \end{equation}

\(\Leftrightarrow\) \begin{equation}\tag{$R_L$}\label{def R_L} \lim\limits_{k\rightarrow \infty} |\ln e_k|^{\frac 1k}=p_0, \end{equation} \(\Leftrightarrow\) \(\forall \varepsilon >0,\ \exists A,B>0, \ 0<\eta,\theta<1, \ k_0 \geq 0\) s.t.

\begin{equation}\tag{$R_{\varepsilon}$}\label{f. def R_eps}
A\cdot \eta^{\left(  p_{0}+\varepsilon \right)  ^{k}}\leq e_k \leq B\cdot \theta^{\left(  p_{0}-\varepsilon \right)  ^{k}%
},\; \; \forall k\geq k_0.
\end{equation}

The C-order is clearly a particular class of the Q-order.

Relevant results can be found in the classical book of [Ortega & Rheinboldt, 1970], and in the book of Potra and Ptak (1984).

Tight connections between these orders were first shown by [Potra 1989], then by [Beyer, Ebanks & Qualls, 1990]. In two recent survey papers, [Catinas, 2019] and [Catinas, 2021] has made a rigorous presentation of all the aspects concerning this topic: definitions, connections, historical, computational aspects.

The connection between the Q- and R-orders can be seen taking \(a_k=\big \vert \ln e_k \big \vert \) in the classical inequalities
\[
\liminf \limits_{k\rightarrow \infty}\frac{a_{k+1}}{a_{k}}\leq \liminf
\limits_{k\rightarrow \infty}\left \vert a_{k}\right \vert ^{\frac{1}{k}}%
\leq \limsup_{k\rightarrow \infty}\left \vert a_{k}\right \vert ^{\frac{1}{k}}
\leq \limsup_{k\rightarrow \infty}\frac{a_{k+1}}{a_{k}}.%
\]

It holds that \(C \Rightarrow Q \Rightarrow R\), i.e., convergence with C-order \(p_0>1\) of a given sequence attracts convergence with Q-order \(p_0\) which in turn attracts convergence with R-order \(p_0\), and none of the converse is true.

Superlinear convergence order (superlinear order of convergence / superlinear rate)

Superlinear convergence order holds when

\[\lim\limits_{k\rightarrow \infty}\textstyle\frac{e_{k+1}}{e_k}=0
\]

In the recent paper [Catinas, 2023], it was shown that there are in fact four types of sequences with strict superlinear order (three of them being in increasing speed).

Linear convergence order (convergence with order one)

The classical linear convergence holds when
\[
\lim \limits_{k\rightarrow \infty} Q_1(k)=Q_1\in(0,1)
\qquad {\rm i.e.,}\
\lim\limits_{k\rightarrow \infty}\textstyle\frac{e_{k+1}}{e_k }=\lim\limits_{k\rightarrow \infty}\frac{| x^\ast – x_{k+1}|}{| x^\ast – x_k |}=Q_1\in(0,1),
\]
and \(Q_1\) is usually called “the convergence rate”.

Computational convergence orders

Instead of errors (usually not known), one may use computable quantities:

• the corrections \(x_{k+1}- x_k \) or
• the nonlinear residuals \(f(x_k)\), when solving iteratively nonlinear equations \(f(x)=0\),

without requiring the knowledge of \(x^\ast\) or \(p_0\).

Let \( s_k := |x_{k+1} – x_k| \), and by denoting \(Q^{\prime}_p(k)=\frac{s_{k+1}}{{s_k}^p}\), construct in the similar way as above the \(C^{\prime}, Q^{\prime}, R^{\prime}\) orders of convergence.

In the same way, let \(f_k := |f(x_k)|\) \(Q^{\prime\prime}_p(k)=\frac{f_{k+1}}{{f_k}^p}\) and construct \(C^{\prime\prime}, Q^{\prime\prime}, R^{\prime\prime}\).

These notations were introduced in [Beyer, Ebanks & Qualls, 1990], the prime mark with no connection to differentiation.

Webpage under construction!!